Оглавление:




Разложение только по косинусам или только по синусам
- Разложение только Косинуса или только синуса. Начнем со следующего замечания: интервальная [- te, K] (непрерывная или по крайней мере непрерывная) функция/(x) есть n E h E t n o y. 7 (x) s1x=0. — ТС. Это легко увидеть один. TC как сумма In-TC TS o tegralov:5+Y и
заменить их на второе-x таким же образом, установлено, что в случае h e t n-й функции/(x ): — С. /(х)г х=2/(х)й х. — Ц0. Здесь пусть/(x) разбивается на интервал[—te, te]h t n A I функция. Далее товар]\х)$ \ н н х н е ч е т н о й функции, где ц НП=^§/(х) z1pgahs/х=0
следующим образом. — l390 глава XXIV. ряд Фурье[405 Поэтому ряд Фурье четной Людмила Фирмаль
функции содержит только косинусы: /(h)-4-2a p S08pH.(15) p 1. В этом случае/(x) так как s o z n x также будет h E t n-й функцией, то, здесь мы применяем второе из вышеприведенных замечаний,мы разложим коэффициенты AP в виде te AP=..да что с тобой такое? (16) функция/
если(x)N E h e t n o y, то n E h e t n o y становится функцией / (x)pop pH, te a » =4g Y/(x) pop l x y x = 0(l-0,1,2,)…да что с тобой такое? — Их Мы приходим к выводу, что ряд Фурье нечетной функции содержит только синус: /(x)=2BP81P pH. (17)n=1 Итак, принимая во внимание четность произведения/(x) z t n x, N= — § / (x) n x y x (n=1, 2, 3,)…да что с
- тобой такое? Заметим, что каждая функция/(x), заданная в интервале (18) [- TS, TS], может быть представлена как сумма четных и нечетных составляющих функции:/(x)= / 1 (x)+A () > Куда? Л (ч) =Ш+я-м\х)=^-^л Ясно, что ряд Фурье функции/(x)состоит из косинусного разложения функции(x) и синусоидального разложения функции/%(x). Кроме того, эта функция/(Х)З А Д А Н А Л И З В П О М Е Т К Е[0, ц]а. Я хочу разложить его в ряд Фурье (2) в этом интервале, но определение
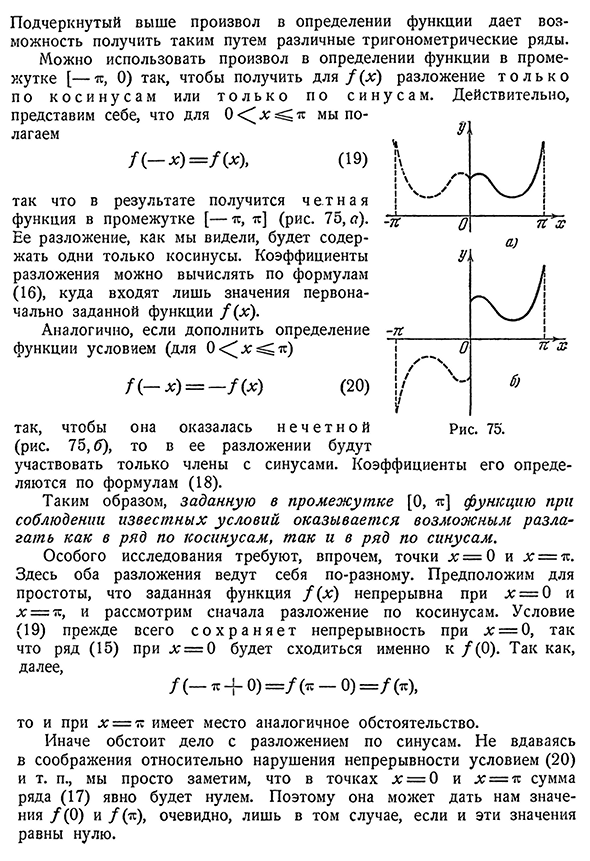
функции для значения x в интервале[—TS, 0) произвольно, но оно сохраняет Дифференцируемость кусочно, и я хочу разложить функцию в n°403.405]§2 ряд Фурье 391. Произвольность, подчеркнутая выше в определении функции, позволяет получить таким образом различные тригонометрические ряды. Представим себе легема, использующего произвольность в определении функции интервала[—te,0), / (x)распада Т О Л К О В К О й н У С а м или Т А Л К О В К О й сам (19) В результате получается интервал H E t n a I [- te, te]. 75, а). в b функция его разложения, как мы видели,
будет содержать только Косинус. Коэффициент разложения может быть вычислен по Людмила Фирмаль
формуле (16), которая изначально содержит только значения заданной функции/(x). Аналогично, если вы добавляете условие к определению функции(0<^x=^te) Действительно., /(- х)=-/(х) (20)н е ч е т н о г (Рис. 75, б), в его разложении участвуют только члены с пазухами. Его коэффициент определяется по формуле (18). Таким образом, заданную интервальной функцией[0, te] при определенных условиях можно разложить как в ряд косинусов, так и в ряд синусов. Однако необходимы специальные исследования, где точки x-0 и x=te. Здесь оба разложения ведут себя по-разному. Предположим для упрощения, что данная функция / (x)непрерывна при x=0 и x=1,
Сначала рассмотрим косинусную факторизацию. Условие (19) сначала гарантирует, что все C o x R a n I e T X=0 в непрерывности, x = 15 в серии 0 сходится точно к/(0). Кроме того, поскольку, / ( _ 1 0) — 0) = / ( « ) , и под x=они поставили аналогичную ситуацию. Это не относится к синусоидальным разложениям. Без учета нарушения продолжения из-за условий(20)и т.д., вы заметите, что с точками x=0 и x=te сумма ряда (17), очевидно, будет равна нулю. Таким образом, вы можете дать значения/(0) и/(1) только в том случае, если эти значения равны
нулю.392 главы XXIV. ряды Фурье[408 Если функция/(x) задана в интервалеРешение задач по математическому анализу
| Случай непериодической функции | Разложение непрерывной функции в ряд тригонометрических многочленов. |
| Случай произвольного промежутка | Интеграл Фурье как предельный случай ряда Фурье |

