Оглавление:
Разложение силы на сходящиеся составляющие
Разложить силу на две или несколько составляющих—значит найти такую систему двух или нескольких сил, равнодействующая которых была бы равна данной силе. При разложении силы, в частности, на сходящиеся составляющие, необходимо, чтобы она по модулю и но направлению изображалась замыкающей стороной силового многоугольника, построенного на составляющих силах как на сторонах.
Так как можно построить бесчисленное множество многоугольников, у которых замыкающий вектор равнялся бы данном силе, то для определенности решения задачи должны быть известны дополнительные условия.
Рассмотрим два, наиболее часто встречающихся, случая.
- Заданную силу
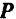требуется разложить на две сходящиеся силы, заданные направления 
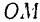и 
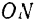которых (рис. 19) лежат в одной плоскости с этой силой.
Для решения задачи из конца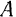 
вектора силы 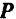проводим прямые 
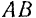и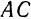 
, соответственно параллельные прямым 
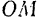и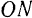 
. Получается параллелограмм 
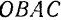, для которого сила 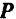является диагональю. Векторы 
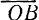и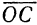 
дают в том же масштабе, что и заданная сила 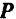, искомые составляющие 
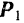и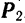 
.
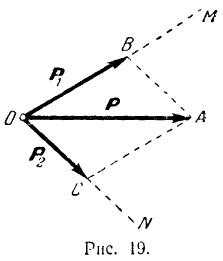
Так как сумма непараллельных сторон параллелограмма всегда больше каждой из его диагоналей, то сумма модулей двух сходящихся составляющих, на которые мы разлагаем заданную силу, всегда больше модуля этой силы.
Чем больше угол между направлениями составляющих сил, тем больше и их модули. При достаточно большом угле между составляющими модуль каждой из них может быть и больше модуля разлагаемой силы.
- Заданную силу 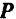требуется разложить на три сходящиеся составляющие, заданные линии действия
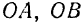и 
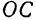которых не лежат в одной плоскости (рис. 20).
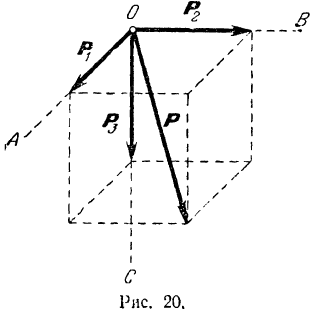
Для решения этой задачи нужно построить параллелепипед, диагональ которого должна изображать по модулю и по направлению заданную силу. Совпадающие с заданными направлениями составляющих ребра этого параллелепипеда будут изображать, в масштабе, принятом для силы 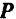, искомые ее составляющие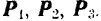 
Пример задачи:
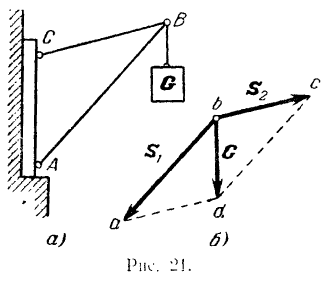
Кран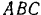 
(рис. 21. а) удерживает груз весом в 
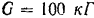. Найти усилия) 
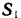и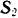 
стержнях 
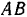и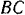 
. Размеры стержней таковы: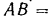 
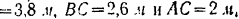
Решение:
Разлагаем силу 
на две составляющие по направлению стержне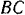й и 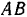, для чего строим параллелограмм 
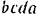(рис. 21.6) со сторонами, параллельными этим стержням, и диагональю 
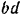, направленной вертикально вниз (соответственно направлению силы тяжести груза).
Длины сторон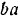 
и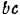 
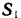построенного параллелограмма дадут нам в том же масштабе, в каким был отложен модуль силы , модули искомых усилии и 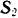. Для вычисления этих условий можно воспользоваться и геометрическими соображениями. Из подобия треугольников 
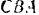и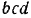 
(рис. 21.а и б) находим:
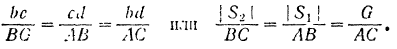
Отсюда
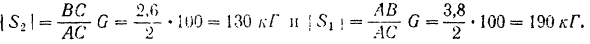
Если учесть направление сил 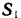к 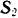. то ясно, что стержень 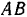испытывает сжатие, а потому 
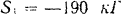стержень 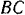растягивается, и следовательно, 
.
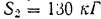Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Связи и реакции связей |
| Геометрический способ сложения сходящихся сил |
| Теорема о равновесии плоской системы трех непараллельных сил |
| Проекции вектора на ось и на плоскость + пример решения |
