Оглавление:
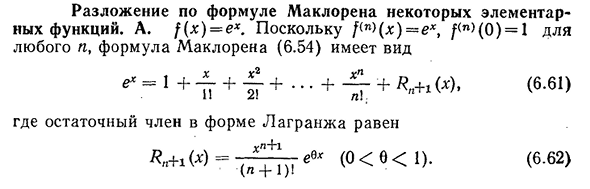





Разложение по формуле Маклорена некоторых элементарных функций.
- Расширение выражения Маклорина на некоторые основные функции. А./(Х)=е. Так как/(0) = 1 для любого p формула Маклорина (6.54) принимает вид 1+Т+ + • • • + + ^ +1 (х)>(6-61)) Где остаточный
член в форме Лагранжа равен(p+LX)=(0—g, g, по факту|E0 / — g, g имеет следующие оценки для остаточного члена: 6/6 4 ) CCH=CO8X. потому что(x) = СОЗ / («) (0)=pop (p4 Отчет п . (-1 ) »
В нечетном р, в четном Р, Людмила Фирмаль
Формула для Маклорина (6.54) имеет форму SO8H= 1 — 4 + 4 — 4 + . . . +(~!В чем дело? 2 4 — + /?»+ , (x), (6.65), где n-четное число, а остаточный член в форме Лагранжа равен ^+2 (h)=4^SO5 (0L+ » t+l) Для любого сегментаМетодическое пособие по математическому анализу
| Первое достаточное условие перегиба | Дифференциалы высших порядков |
| Формула Маклорена | Понятие модуля непрерывности функции |

