Оглавление:
Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции 
в ряд Маклорена (64.3) нужно:
а) найти производные 
;
б) вычислить значения производных в точке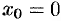 
;
в) написать ряд (64.3) для заданной функции и найти его интервал сходимости;
г) найти интервал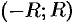 
, в котором остаточный член ряда Маклорена 
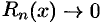при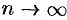 
. Если такой интервал существует, то в нем функция и сумма ряда Маклорена совпадают.
Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при .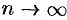
Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
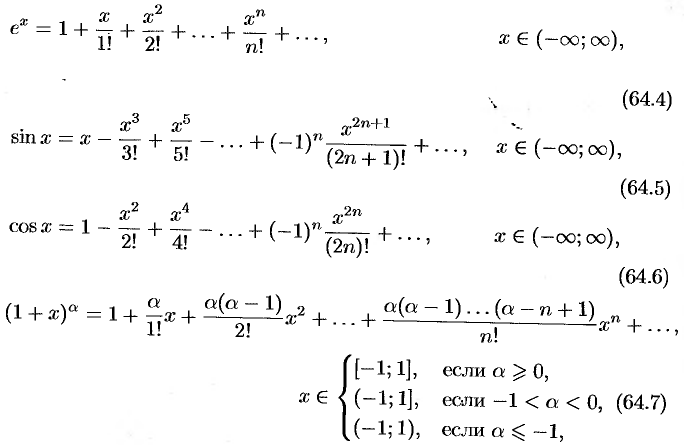
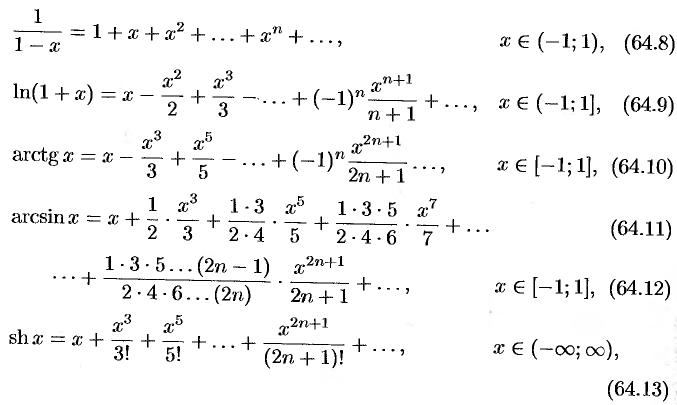
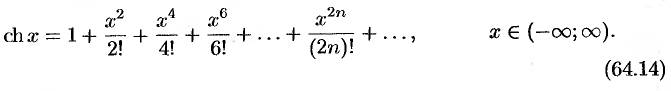
Докажем формулу (64.4). Пусть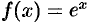 
.
Имеем:
а)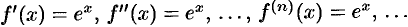 
;
б)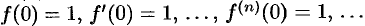 
;
в)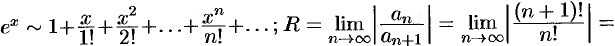 
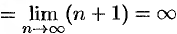, т. е. ряд сходится в интервале 
;
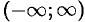г) для всех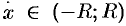 
имеем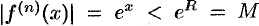 
, т. е. все производные в этом интервале ограничены одним и тем же числом 
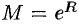. Следовательно, по теореме 64.2 
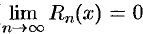. Таким образом,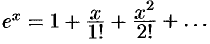 
Докажем формулу (64.5). Пусть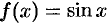 
.
Имеем:
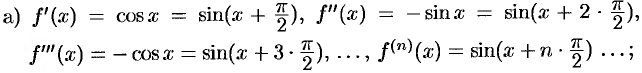
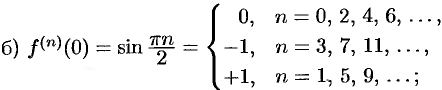
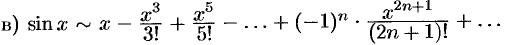Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех 
;
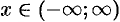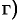любая производная функции 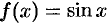по модулю не превосходит единицы, 
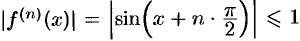. Следовательно, по теореме 64.2 имеет место разложение (64.5).
Докажем формулу (64.6). Пусть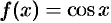 
.
Формулу (64.6) можно доказать так же, как и формулу (64.5). Однако проще получить разложение функции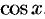 
, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (64.5), получим:
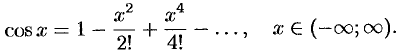
Докажем формулы (64.13), (64.14). Пусть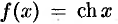 
(или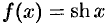 
).
Заменив в формуле (64.4) 
на 
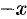, получим разложение функции 
:
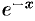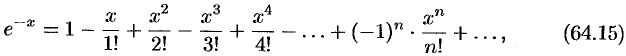
справедливое для всех .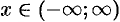
Суммируя (и вычитая) почленно равенства (64.4) и (64.15), получим разложение гиперболического косинуса (синуса):
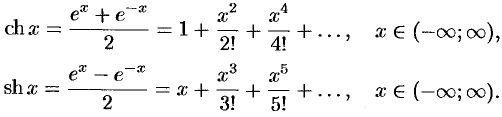
Формулы (64.13) и (64.14) доказаны.
Докажем формулу (64.7). Пусть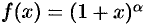 
, где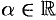 
.
Имеем:
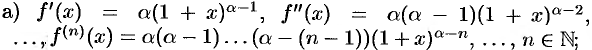
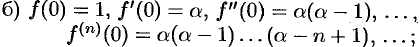
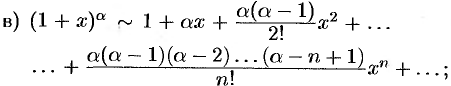
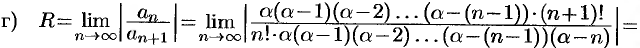
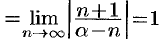, т. е. составленный для функции 
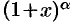ряд сходится в интервале (—1; 1).
Можно показать, что и в данном случае, т.е. при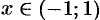 
, остаточный член 
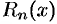стремится к нулю при .
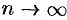Ряд (64.7) называется биномиальным. Если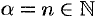 
, то все члены ряда с 
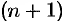-го номера равны 0, так как содержат множитель 
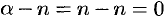. В этом случае ряд (64.7) представляет собой известную формулу бинома Ньютона:
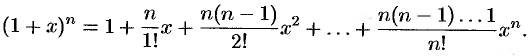
Докажем формулу (64.8). Пусть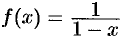 
.
Формула (64.8) может быть получена разными способами:
1) пользуясь правилом разложения функции в ряд;
2) рассматривая ряд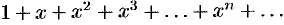 
как ряд геометрической прогрессии, первый член которой равен единице и знаменатель 
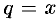; известно (см. пример 62.1), что данный ряд сходится при 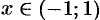и его сумма равна 
;
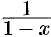3) воспользовавшись формулой (64.7): положив в ней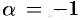 
и заменив на 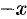, получим формулу (64.8).
Докажем формулу (64.9). Пусть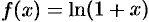 
.
Формула (64.9) также может быть доказана разными способами. Приведем один из них.
Рассмотрим равенство
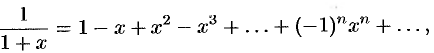
справедливое для всех 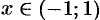. Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке 
, :
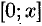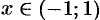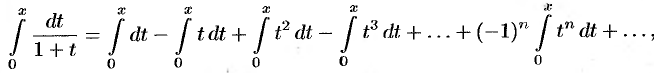
или
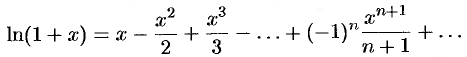
Можно показать, что это равенство справедливо и для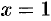 
.
Докажем формулу (64.10). Пусть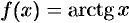 
.
Положив в формуле (64.7) 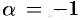и заменив на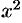 
, получим равенство
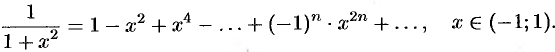
Тогда
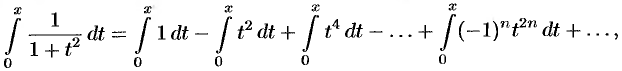
или
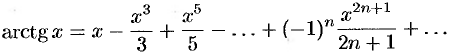
Можно показать, что равенство справедливо и при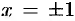 
, т. е. при всех 
.
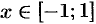Докажем формулу (64.12). Пусть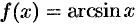 
.
Положив в формуле (64.7)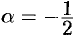 
и заменив на (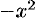
), получим равенство
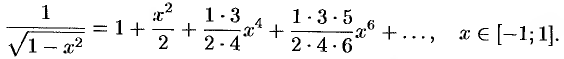
Тогда
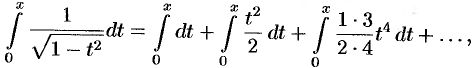
или
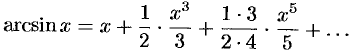
Можно показать, что полученное равенство справедливо при всех .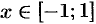
Ряды (64.4)-(64.14) в комбинации с правилами сложения, вычитания, умножения, дифференцирования, интегрирования степенных рядов (см. свойства степенных рядов) могут быть использованы при разложении (некоторых) других функций в ряд Маклорена (Тейлора).
Пример №64.1.
Разложить в ряд Маклорена функцию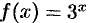 
.
Решение:
Так как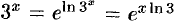 
, то, заменяя на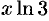 
в разложении (64.4), получим:
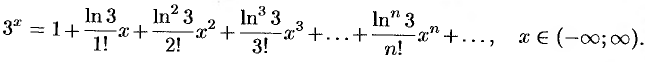
Пример №64.2.
Выписать ряд Маклорена функции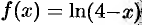 
.
Решение:
Так как
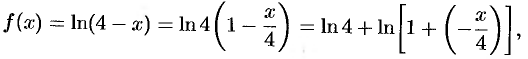
то, воспользовавшись формулой (64.9), в которой заменим на (
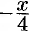) получим:
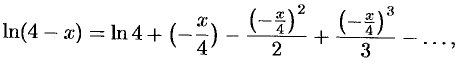
или
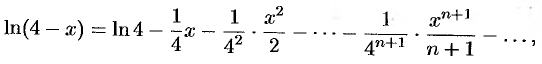
если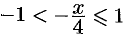 
, т. е. 
.
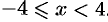Пример №64.3.
Разложить в ряд Маклорена функцию
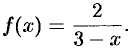
Решение:
Воспользуемся формулой (64.8). Так как
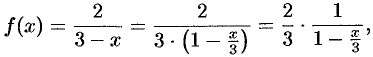
то, заменив на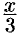 
в формуле (64.8), получим:
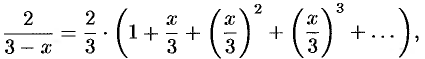
или
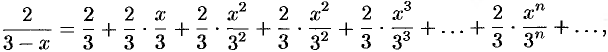
где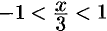 
, т. е. 
.
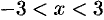На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление поверхностного интеграла II рода |
| Некоторые приложения поверхностного интеграла II рода |
| Некоторые приложения степенных рядов |
| Приближенное вычисление определенных интегралов |
