Разложение эпюр на составляющие треугольной и параболической форм.
Любую эпюру изгибающих моментов при загружении балки сосредоточенными силами, моментами и равномерно распределенными нагрузками всегда можно представить как сумму эпюр треугольного и параболического очертания (рис. 101).
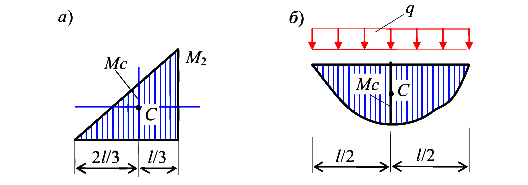
Эпюры, приведенные на рисунке 101, мы можем назвать элементарными или простыми, так как для них легко определяется положение центра тяжести и площади.
Площадь и центр тяжести треугольной эпюры (рис. 101, а)
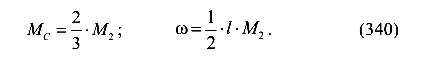
Площадь и центр тяжести параболической эпюры (рис. 101,б)
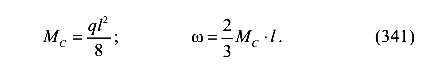
Покажем возможные варианты разложения эпюр (рис. 102) и (рис. 103)
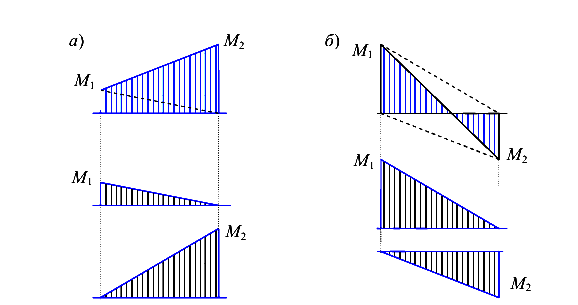
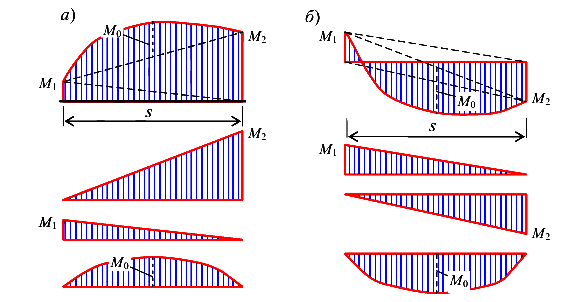
перекрученной (б)трапеции
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Определение перемещений методом Максвелла-Мора |
| Вычисление интеграла Мора способом Верещагина |
| Статически неопределимые системы |
| Понятие об основной системе метода сил |

