Разложение движения плоской фигуры на поступательное и вращательное

Разложение движения плоской фигуры на поступательное и вращательное. Зависимость между скоростями различных точек фигуры

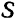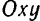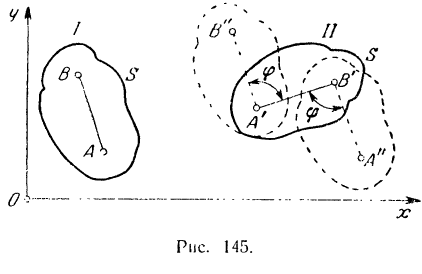
Пусть какая-либо плоская фигура движется в плоскости и за некоторый промежуток времени 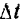перемещается из положения I в положение II (рис. 145). Это перемещение фигуры 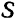и неизменно связанного с ней отрезка 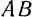можно представить себе составленным из поступательного и вращательного перемещении.

В самом деле, перемещение отрезка 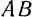в положение 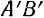(а следовательно, и перемещение фигуры 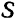из положения I в положение II) можно получить его поступательным перемещением в положение 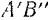, а затем поворотом этого отрезка на некоторый угол 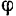вокруг полюса— точки 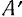. С одинаковым успехом ,»а полюс можно было бы выбрать любую другую точку фигуры, например, точку 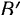и перемещение фигуры из положения I в положение II осуществить поступательным перемещением отрезка 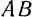в положение 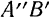, а затем поворотом его вокруг точки 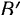до совмещения с отрезком .

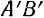Важно заметить, что угол поворота и направление вращения фигуры не зависят от выбора полюса.

Из рис. 145 ясно, что 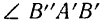поворота, совершаемый отрезком 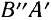при переходе его в положение 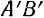вращением вокруг полюса 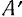, равен 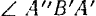поворота, совершаемому отрезком 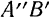при переводе его в то же положение 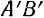вращением вокруг полюса 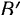. Одинаковым будет и направление вращения (па рис. 145 по ходу стрелки часов). К тому же результату мы придем, если примем за полюс любую иную точку, связанную с движущейся фигурой .

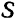Произведенная выше замена движения фигуры 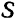за некоторый конечный промежуток времени 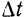двумя последовательными (поступательным и вращательным) перемещениями не воспроизводит, вообще говоря, действительного движения фигуры. При помощи такой замены мы получаем лишь тот же самый конечный результат — то же самое положение фигуры в конце рассматриваемого промежутка времени.

Для того чтобы воспроизвести фактическое движение фигуры за некоторый конечный промежуток времени, разобьем его на большое число очень малых промежутков и отметим те положения, которые занимает фигура в конце каждого из этих промежутков. Выбрав какую-либо произвольную точку фигуры за полюс, будем осуществлять переход фигуры и:; каждого данного положения в близкое ему соседнее путем поступательного перемещения фигуры, соответствующего перемещению выбранного полюса, и вращательного перемещения фигуры вокруг полюса. Непрерывно увеличивая число промежутков времени и тем самым уменьшая их величину, мы будем проводить фигуру через все большее и большее число положений, которые она на самом деле занимает в конце каждого из малых промежутков времени. В пределе, когда величина этих промежутков времени будет стремиться к нулю, мы проводом фигуру через все положения, которые она занимает при своем фактическом движении. Таким образом, мы приходим к выводу: всякое движение плоской фигуры в ее плоскости можно разложить на два движения: 1) поступательное движение со скоростью произвольно выбранной точки фигуры (полюса) и 2) вращательное движение вокруг полюса.

По аналогии с представлениями о сложном движении точки, поступательное движение фигуры 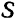(рис.145) вместе с полюсом относительно неподвижных осей 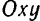можно назвать переносным движением фигуры; вращательное движение фигуры вокруг полюса, неизменно связанного с движущейся фигурой, — относительным движением фигуры, а ее результирующее движение относительно неподвижных осей 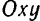— абсолютным движением.

Так как различные точки фигуры движутся, вообще говоря, с различными скоростями, то переносное поступательное движение фигуры зависит от выбора полюса.

Выше было показано, что угол 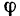поворота фигуры и направление ее вращения не зависят от выбора полюса. Отсюда следует, что и угловая скорость фигуры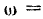 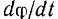и ее угловое ускорение 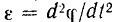от выбора полюса не зависят.

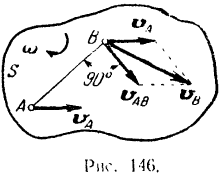
Пусть некоторая плоская фигура 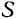движется в ее плоскости (рис. 146). Примем какую-либо произвольную точку 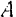этой фигуры за полюс. Тогда можно считать, что но отношению к неподвижной системе отсчета (связанной с плоскостью, в которой движется фигура) любая другая точка 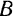фигуры участвует одновременно в двух движениях: переносном — вместе с фигурой в ее поступательном движении со скоростью 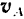выбранного полюса и относительном — вращательном движении вокруг полюса 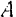с угловой скоростью 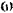, не зависящей от выбора полюса.

Отсюда, на основании теоремы о сложении скоростей, имеем, что абсолютная или просто, как мы ее будем называть в дальнейшем, скорость любой точки плоской фигуры в каждый момент равна геометрической сумме двух скоростей, скорости другой, произвольно выбранной точки фигуры (полюса) и скорости от орошения первой точки относительно второй:

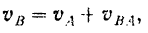
где 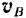— скорость любой точки 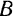плоской фигуры, и 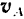— скорость другой произвольной точки (полюса) 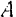фигуры, 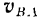— скорость первой точки относительно второй (полюса).

Скорость точки 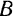относительно точки 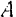легко найти по модулю и по направлению, если известны для данного момента времени угловая скорость фигуры и положение точек 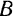и 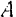. Модуль этой скорости

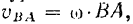
где 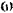— угловая скорость фигуры, 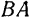— расстояние между точкам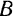и и 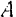. Направлена же скорость 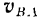перпендикулярно к соответствующему радиусу вращения (т.е. к отрезку 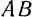) в сторону вращения фигуры (на рис. 146 стрелкой показано, что фигура вращается по ходу стрелки часов).

Определив скорость 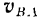точки 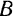относительно полюса и зная скорость 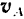самого полюса, находим искомую скорость точки 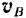как диагональ параллелограмма, построенного на векторах 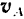и 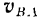составляющих скоростей (рис. 146).

Заметим, что формулой (100) устанавливается зависимость между скоростями двух каких угодно точек плоской фигуры, причем за полюс может быть выбрана любая из этих точек. Обычно за полюс принимается та точка фигуры, скорость которой в данный момент нам известна.

Пример задачи:

Стержень 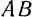(рис. 117) движется и плоскости 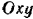так, что нижний его конец 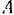скользит по оси 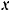, а сам стержень касается вертикального столба 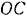. Для момента, когда ось стержня 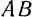наклонена к оси 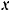под углом 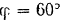и скорость нижнего конца стержня 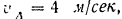, определить скорость тон точки 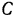стержня. в которой он касается столба, а также угловую скорость 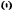стержни. Высота столба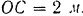

Решение:

Стержень 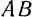совершает плоское движение. Скорость одной его точки, точки 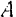, нам известна. Принимаем эту точку за полюс. Тогда скорость другой точки 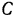стержня

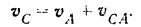
Скорость точки 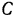относительно точки 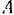будет равна по модулю

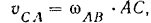
где 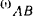— угловая скорость стержня 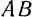. Направлена же скорость 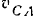перпендикулярно к отрезку 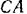в сторону его вращения. Так как точка 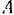движется по оси 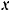вправо, то угол 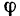будет при этом движении уменьшаться и, следовательно, вращение стержня 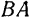направлено против часовой стрелки. Таким образом, направление скорости мы знаем. Так как в точке 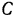стержень касается столба, то скорость 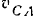этой точки может быть направлена только вдоль стержня. С другой стороны, вектор должен являться диагональю параллелограмма, построенного на

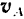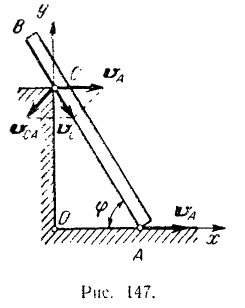
векторе (известном нам по модулю и по направлению) и на векторе 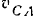(известном нам по направлению) как на сторонах. Но данным условиям можно построить только один параллелограмм (рис. 147). Так как угол между 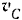и 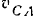— прямой, то из прямоугольного треугольника находим’

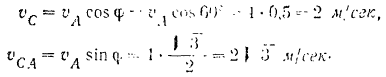
Из прямоугольного треугольника 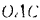находим длину отрезка 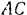для данного момента:

Угловая скорость стержня 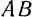в данный момент равна

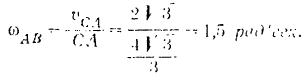
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Теоретическая механика — задачи с решением и примерами

Возможно вам будут полезны эти дополнительные темы:

Понятие плоского движения тела

Уравнения движения плоской фигуры + пример с решением

Теорема о проекциях скоростей двух точек фигуры + пример с решением

Мгновенный центр скоростей фигуры