1) Уравнение вида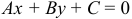 
с произвольными коэффициентами 
, 
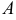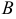и 
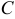, такими, что 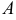и 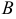не равны одновременно нулю, называется общим уравнением прямой.
Общее уравнение прямой называется полным, если все его коэффициенты 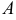, 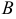и 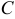отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, уравнение называется неполным.
a) Если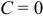 
, то уравнение 
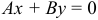определяет прямую, проходящую через начало координат.
b) Если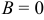 
, то уравнение 
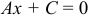определяет прямую, параллельную оси 
.
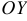c) Если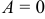 
, то уравнение 
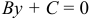определяет прямую, параллельную оси 
.
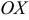2) Полное уравнение прямой может быть приведено к уравнению прямой «в отрезках» на осях
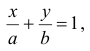
где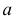 
и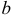 
— это отрезки, отсекаемые прямой на осях 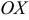и .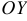
Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой.
3) Уравнение прямой, проходящей через точку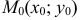 
перпендикулярно вектору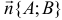 
, имеет вид
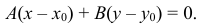
4) Уравнение прямой, проходящей через две точк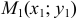и 
и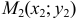 
имеет вид:
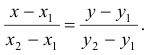
5) Каноническим уравнением прямой называют уравнение вида
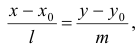
где 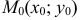— координаты точки, принадлежащей прямой; 
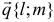— координаты направляющего (параллельного прямой) вектора.
6) Из канонического уравнения прямой можно элементарно получить параметрические уравнения прямой. Примем за параметр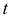 
величину, стоящую в левой и в правой частях канонического уравнения прямой, тогда:
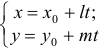— параметрические уравнения прямой.
Параметрические уравнения прямой имеют наглядную физическую интерпретацию. Если считать, что параметр 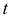— это время, отсчитываемое от некоторого начального момента, то параметрические уравнения определяют закон движения материальной точки по прямой линии с постоянной скоростью 
.
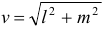7) Уравнение прямой, проходящей через заданную точку 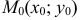и имеющей угловой коэффициент 
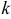, имеет вид:
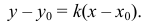
Угловым коэффициентом называют тангенс угла наклона прямой к оси .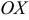
8) Уравнение вида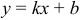 
называют уравнением прямой с угловым коэффициентом.
9) Уравнение вида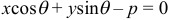 
называют нормированным уравнением прямой, где 
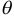— угол между нормальным вектором прямой и осью ;
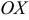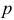— расстояние от начала координат до прямой.
Отклонение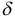 
произвольной точки 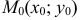от прямой определяется:
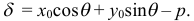
Чтобы вычислить расстояние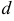 
от точки 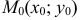до прямой, достаточно вычислить отклонение 
.
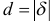Расстояние от точи 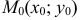до прямой 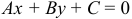, заданной общим уравнением, вычисляется по формуле 
.
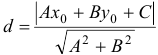Чтобы привести общее уравнение прямой к нормированному виду, нужно все члены этого уравнения умножить на нормирующий множитель
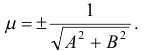
Знак нормирующего множителя выбирается противоположным знаку свободного члена общего уравнения прямой.
10) Уравнение вида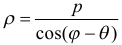 
называется полярным уравнением прямой, где 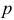— расстояние от полюса до прямой; 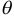— угол между нормалью прямой и полярной осью.
Совокупность прямых, проходящих через некоторую точку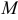 
, называют пучком прямых с центром в точке .
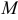11) Уравнение пучка прямых имеет вид
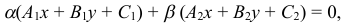
где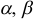 
— любые числа, не равные одновременно нулю.
12) Векторное уравнение прямой имеет вид
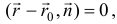
где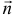 
— нормальный вектор прямой; 
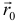— радиус вектор точки 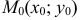, принадлежащей прямой; 
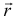— радиус вектор произвольной точки 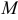, принадлежащей прямой.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Векторное и смешанное произведения в декартовых координатах |
| Алгебраические линии и поверхности |
| Определение угла между прямыми |
| Различные виды уравнения плоскости |
