1) Уравнением плоскости, проходящей через точку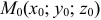 
перпендикулярно вектору 
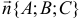, называют уравнение вида
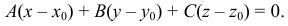
2) Общее уравнение плоскости в прямоугольной системе координат имеет вид
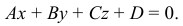
Общее уравнение называют полным, если все его коэффициенты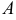 
, 
, 
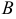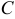и 
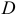отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, уравнение называется неполным.
- Если
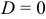, то уравнение 
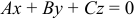определяет плоскость, проходящую через начало координат. - Если
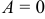, то уравнение 
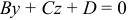определяет плоскость, параллельную оси 
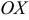. - Если
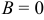, то уравнение 
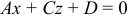определяет плоскость, параллельную оси 
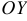. - Если
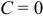, то уравнение 
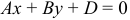определяет плоскость, параллельную оси 
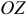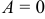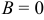. - Если и , то уравнение
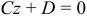определяет плоскость, параллельную плоскости 
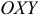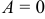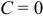. - Если и , то уравнение
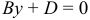определяет плоскость, параллельную плоскости 
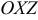. - Есл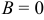и и 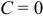, то уравнение
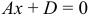определяет плоскость, параллельную плоскости 
.
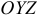3) Полное уравнение плоскости может быть приведено к уравнению плоскости «в отрезках» на осях
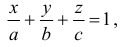
где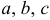 
— отрезки, отсекаемые плоскостью на осях 
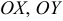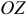, соответственно.
4) Уравнение плоскости, проходящей через три точки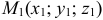 
,
, 
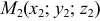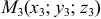, имеет вид
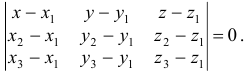
Уравнение представляет собой условие компланарности векторов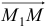 
, 
, 
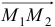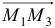, где точка 
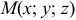— произвольная точка на искомой плоскости.
5) Нормированное уравнение плоскости имеет вид
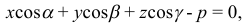
где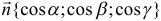 
— единичный нормальный вектор искомой плоскости; 
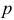— расстояние от плоскости до начала координат.
Подставив координаты произвольной точки 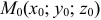в нормированное уравнение, найдем отклонение 
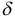точки от плоскости:
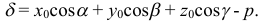
Тогда расстояние от точки 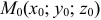до плоскости равно 
.
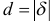Если плоскость задана в общем виде, то расстояние от точки 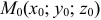до плоскости определяется уравнением
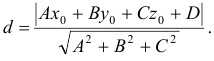
6) Векторное уравнение плоскости определяется скалярным произведением:
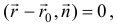
где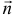 
— нормальный вектор; 
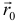— радиус-вектор точки 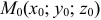, принадлежащей плоскости; 
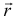— радиус-вектор любой точки плоскости.
Совокупность всех плоскостей, проходящих через одну и ту же прямую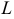 
называется пучком плоскостей с центром .
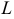7) Уравнение пучка всех плоскостей, проходящих через линию 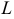, имеет вид
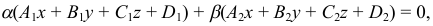
где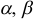 
— любые числа, не равные одновременно нулю.
Совокупность всех плоскостей, проходящих через одну и ту же точку 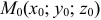, называется связкой плоскостей с центром в точке .
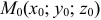8) Уравнение связки плоскостей с центром в точке 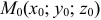имеет вид
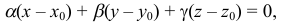
где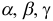 
— любые числа, не равные одновременно нулю.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Различные виды уравнения прямой на плоскости |
| Определение угла между прямыми |
| Угол между плоскостями |
| Прямая линия в пространстве |
