Различные виды уравнений прямой в пространстве

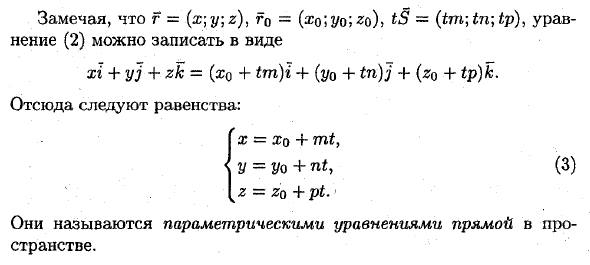
Различные виды уравнений прямой в пространстве

• Различные типы уравнений, которые существуют непосредственно в космосе 1. Линейное векторное уравнение Установка точки Мо на линии и вектора S, параллельного этой линии, будет четко определять положение линии в пространстве. Вектор S называется вектором направления линии. Предположим, что прямая L задается своей точкой Mo (x0 \ y0) z0) и вектором направления 5 = (w; n; p). Возьмем произвольную точку M (x \ y \ z) на прямой L. Радиус-векторы точек Mo и M представлены r и r соответственно.

Следовательно, MqM = tS (t — скалярный коэффициент, называемый параметром) может принимать различные значения в зависимости от положения точки M на прямой. Уравнение (1) r = r0 + tS. (2)

Очевидно, что три вектора ^, f, M0M r = r0 + M0M. (1) Вектор MoM на линии L параллелен вектору направления S. Людмила Фирмаль

Результирующее уравнение называется линейным векторным уравнением. 2. Параметрические уравнения прямых Обратите внимание, что r = {x \ y \ r), r0 = (x0; y0; tS = (tm; tn; tp) и выражение (2) можно записать в следующем виде: xi + yj + zk— (z0 + tm) i-f (y0 + tn) j-f (z0 + tp) k. Равенство продолжается отсюда: х = хо + т, y = g / o + nty (3) Z-Zq + pt. > Они называются параметрическими уравнениями для линий пространства.

Линия канонических уравнений Пусть 5 = ​​(m; n; p) — вектор направления линии L, а Mo (x0; / / o; ^ o) — точка на этой линии. Вектор MoM, соединяющий точку Mo и любую точку M (x \ y \ z) на прямой L, параллелен вектору S. Таким образом, вектор MqM = (x-xo; y-yo] z-zo) и вектор S = (y / g; p; p) пропорциональны: x-Xq _ y-yo z-Zp t p p Уравнение (4) называется каноническим уравнением для прямой в пространстве. Примечания: 1) Уравнение (4) можно получить непосредственно из параметрического уравнения в строке (3), за исключением параметра t.

• Решение задач по высшей математике

Различные виды уравнений плоскости в пространстве	Прямая линия в пространстве. Основные задачи
Плоскость. Основные задачи	Прямая и плоскость в пространстве. Основные задачи

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Из уравнения (3) x-xp _ y -you _z-z0 t t p p 2) Исчезновение одного из знаменателей в уравнении (4) означает исчезновение соответствующего числителя. Например, уравнение ^ = — = 2 ~ ^ определяет линию, Он проходит через точку M0 (2; -4; 1), перпендикулярную оси Oz (проекция вектора S на ось Oz равна нулю). Но это означает, что прямая находится в плоскости n = 1. Следовательно, 2-1 = 0 во всех точках на линии.

В качестве вектора направления 5 вектор MlM-2- {X2-Xi \ y2-2 / 1; Z2-Z ), то есть 5 = M \ A / 2. В результате m = -x \, n = 3 / 2-2 / 1 »p = 2: 2-z . Линия проходит через x / ^ и проходит через точку Mi (xi; yi; zi), поэтому согласно формуле Уравнение (4), форма уравнения для линии L имеет вид x-xi _ y-y / 1 _ z-zi ^ «Си Y2-Y \ Z2-Zi» Уравнение (5) называется линейным уравнением через две заданные точки.

Линейное уравнение в космическом проходе Через две точки Пусть линия L пройдет через точки M \ (xi \ yi \ z {) и Mm (x2 \ Y2 \ Z2). Людмила Фирмаль

Общее уравнение прямой Прямая в пространстве может быть определена как пересечение двух непараллельных плоскостей. Рассмотрим одновременные уравнения Ex + Bxy + Ciz + Di = 0, Л2х + В2у4- C2z 4- D2 = 0 Каждое уравнение в этой системе определяет плоскость. Если плоскости не параллельны (координаты вектора ni = (A \ B \ C ) и n2 = (A2 \ B2 \ C2) не пропорциональны), система (b) является точкой фв ​​пространстве, которой удовлетворяет координата L Каждое уравнение линии L системы как траектория. Уравнение (6) называется общим уравнением для прямой.

Из общего уравнения (6) можно перейти к каноническому уравнению (4). Координаты точки Мо на линии L берутся из системы уравнений (6) и дают одной из координат произвольное значение (например, r = 0). Поскольку прямая L перпендикулярна векторам nx и n2), векторное произведение nx x n2 может быть получено для вектора направления 5 прямой линии L. к г Любовь A2 3 B1 B2 Ci c2 x n2 = S = ты Примечание. Стандартное уравнение прямой можно легко получить, взяв любые две точки и применив уравнение (5). Пример: написать каноническое уравнение для линии L, заданное уравнением x + y-z + 1 = 0, 2x-y-3z + 5 = 0 (6)

Найти очки y-z = -1, -y-32 = -5. Найдите вторую точку Mg (0; –4; –3) на прямой L. Напишите уравнение для линии L через точки M1 и M2. x + 2_y-l_ z 2 ~ -5 ~ ^ 3 * х + у = -1 ♦ Установите z = 0 и решите систему 2 ху = -5. Mi (-2; 1; 0) € L. Решите систему с x = 0 <