Оглавление:



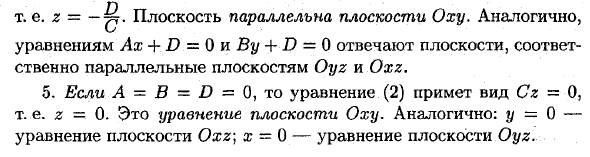



Различные виды уравнений плоскости в пространстве
- РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЙ ПЛОСКОСТИ В ПРОСТРАНСТВЕ Простейшая поверхность является плоскость. Плоскость в пространстве Oxijz можно задать разные способы. Каждая из них соответствует определенному виду ее уравнение. 1. Уравнение плоскости, проходящей через точку точки перпендикулярно существующего вектору Пусть в пространстве Oxyz плоскость Q задана точкой Mq {XQ \ уо; зо) и вектором п = (А ;. В \ С), перпендикулярным этой плоскости
Выведем уравнение плоскости Q. При любом расположении точки М на плоскости Q векторы п и ДМК взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: п • ДМК = 0, т е , А (х-®0) + В (у-у0) + С (z-z0) = 0. (1) Координаты любой точки плоскости Q удовлетворяют (1), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них п • Л / о М ф 0).
Возьмем на ней произвольную точку М {х \ у \ г) .. и составим вектор М0М = (ж — х0 \ у — у0; г — ZQ) Людмила Фирмаль
Уравнение (1) называется уравнением плоскости, проходящей через данную точку Mq (хо \ уо; ZQ) .перпендикулярно вектору п =. (Л; В; С) Оно первой степени относительно текущих координат ху у и г. Вектор п — (А \ В \ С) называется нормальным вектором плоскости. .. Придавая коэффициентам А, В и С уравнения (1) различные значения, можно получить уравнение любой плоскости, проходящей через точку Mq Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей а уравнение (1) — уравнением связки плоскостей.
Рассмотрим общее уравнение первой степени с тремя переменными х, у vi z: (2) Ax + By + Cz + D = 0. Не равны нулю, например, В и 0, пеме (3) Сравнивал уравнение (3) с уравнением (1), видим, что уравнения (2) и (3) являются уравнением плоскости с нормальным вектором п = (А; В) С), проходящей через точку М \ (0; — Q; 0 ). Итак, уравнение (2) определяет в системе координат Oxyz некоторую плоскость.
| Общее уравнение линий второго порядка | Плоскость. Основные задачи |
| Поверхности и линии в пространстве и их уравнения | Различные виды уравнений прямой в пространстве |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Частные случаи общего уравнения плоскости: 1. Если D = 0, то оно принимает вид Ах -f К + Cz = 0. Этому уравнению удовлетворяет точка 0. (0; 0; 0) Следовательно, в этом случае плоскость проходит через начало координат. . 2. Если С = 0, то имеем уравнение Ах -f- К + D = 0. Нормальный вектор п = {А; В; 0) перпендикулярен оси Оз Следовательно, плоскость параллельна оси Oz; если В = 0 — параллельна оси Оу , А = 0-параллельна ос Ох. 3. Если С = D = 0, то плоскость проходит через 0 (0; 0) 0 + Cz = 0. 4. Если А = В = 0, то уравнение (2) принимает вид Cz + D = 0} + C (z-0) = 0.
т. е. 2 = — ^ 4. Плоскость параллельна плоскости Оху. уравнениям Ax + D = 0nBy + D = 0 взаимодействующих плоскостей, соответственно параллельных плоскостям Oyz и Ox yz 5. Если А = В = D = 0, то уравнению (2) примет вид Cz-О, т. Е. Z-0. Плоскости Oyz.
. Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость Найдем уравнение плоскости Q, проходящей через три данные точки Ми (XI; ил] Zi), М2 (х2; 2 / 25z2) и М3 (х3-, у3]. гз), не лежащие на одной прямой.
Уравнение плоскости, проходящей через три данные точки Людмила Фирмаль
Возьмем на плоскость спутника точку М (х; у; z) и составим предлагаемую MiM = (x-xi \ y-yi \ z- ~ zi), М \ М2y =) М \ М2y =) \ уг — 2/1; 2: 3 ~ 21) Эти векторы лежат на плоскости Q, следовательно, они компланарны Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем М \ М • М \ М2 • М \ М $ = 0, т. х-хх у-т / 1 z- Zi Xl -XI У2- У \ z2-Zi Хг -Xl 2/3-й Zt-Zi (4) = 0 Уравнение (4) есть уравнение плоскости, проходящее через три данные точки. 4. Уравнение плоскости в отрезках
Уравнение плоскости в отрезках Пусть плоскость пересекается на осях Ох, Оу и Оз соответственно соответственно отрезки, Ъ и с, т. П. Проходис Подставляя координаты этих точек в уравнение (4), получаем Раскрыв определитель, у нас hex-abc + abz -f асу = 0, т. Е. Ящик -I- асу 4- abz = abc или — +! + — =! • (5) азбука Уравнение (5) называется уравнением плоскости в отрезках на осях.
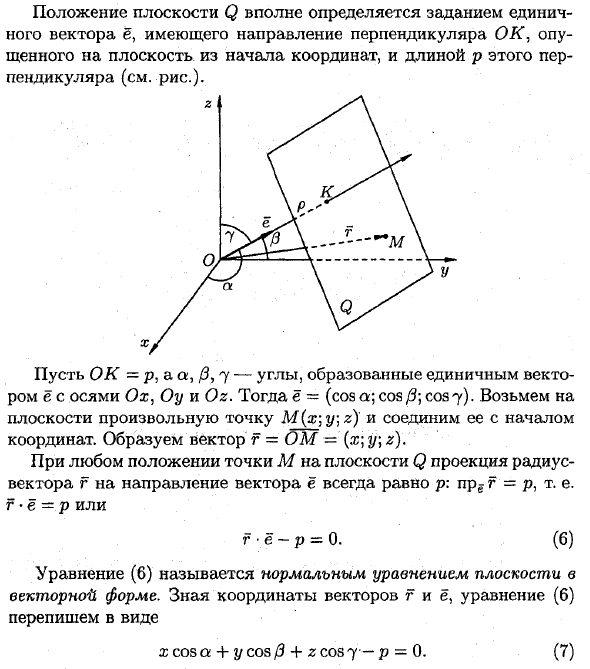
ПОЛОЖЕНИЕ В плоскости вполне определяется заданием единичного вектора ё, имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (см. Рис.). х
Пусть О К = р, а а, / 3,7 -. Углы, образованные единичный вектор с осями Ох, Оу и 02. Тогда ё = (потому что <* (х \ у \ г) и вектор с начало координаты Образует вектор f = ОМ = (x \ y \ z). В любом положении точки на плоскости Q (Б) (7) f • е-р = 0. Уравнение (6) называется нормальным уравнением плоскости в векторной форме. zcosa + 2 / cos / 3 + zcosy-p = 0.
Уравнение (7) называется нормальным уравнением плоскости в ко-ординатной форме. Отметим, что общее уравнение плоскости (2) можно привести к нормальному уравнению (7) так, как это делалось для уравнения прямой на плоскости А именно :. Умножить обе части уравнения (2) на нормирующий множитель Л = -, », где знак берет- ± у / А2 + В2 + С2.

