Равновесие тел при наличии трения

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

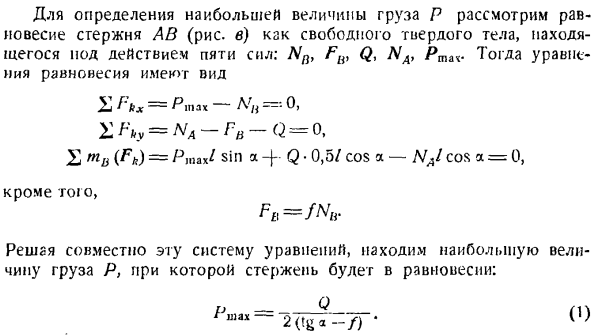
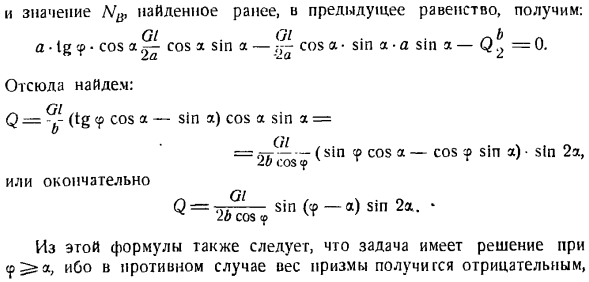
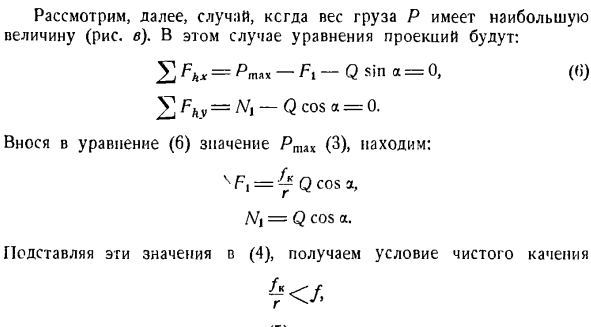
Равновесие тел при наличии трения

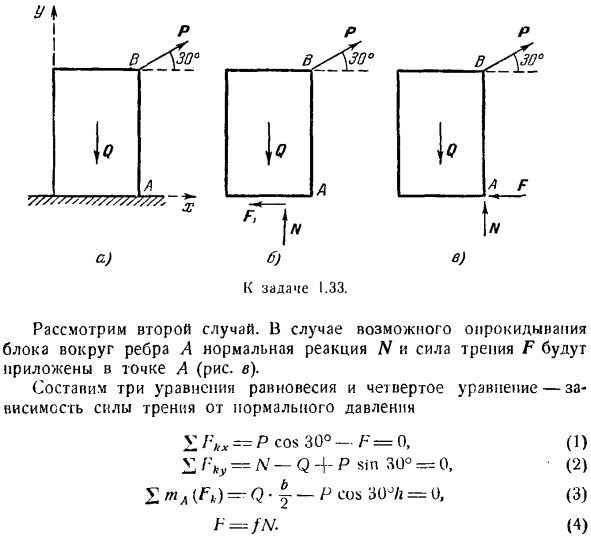
Баланс тела, когда есть трение Н-М = 0, Т-Ф = 0. (1*) (2 *） 1°.Равновесие твердых тел при наличии трения скольжения. Если в результате действия активной силы возникает сила трения скольжения, создаваемая между шероховатым объектом и шероховатой поверхностью, не перпендикулярной поверженной поверхности (рис.1.36).Когда объект находится в равновесии, реакция на шероховатой поверхности 5 (Рис.1.37) должна быть величиной R и направлена в противоположную сторону.

Действующая сила R разлагается на нормальную составляющую N и касательную составляющую T, реакцию{и касательную составляющую F шероховатой поверхности относительно нормальной составляющей N. Это называется силой трения скольжения или 1-м типом трения force.

В состоянии равновесия, равенство должно соблюдаться. Людмила Фирмаль

Чтобы найти величину силы P, достаточно найти значение из(3). p_ Ob _ 200_0 / b. два_ 1-2 часа cos 30° — G OYA’uz〜 ’ Когда коэффициент силы P больше этого значения, блок начинает падать рядом с ребром A. Выражение（1）、（2）、（4）может использоваться для определения вертикальной силы реакции и силы трения. Если сравнить по модулю р значение силы первого и второго случая, то величина силы Р при скольжении меньше значения в момент опрокидывания, поэтому при увеличении модуля силы р от нуля до максимума блок не опрокидывается первым.

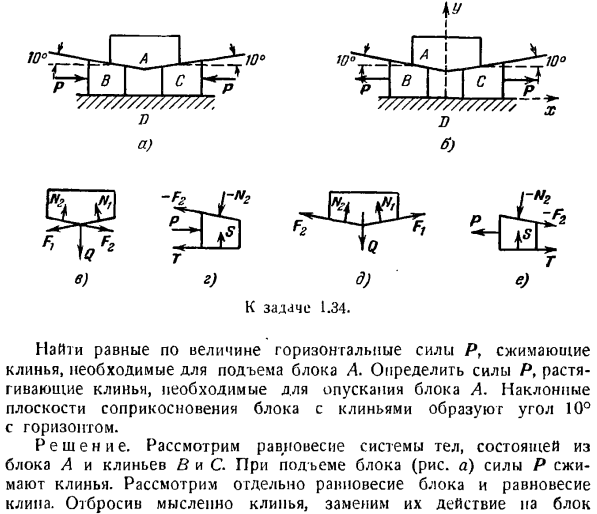
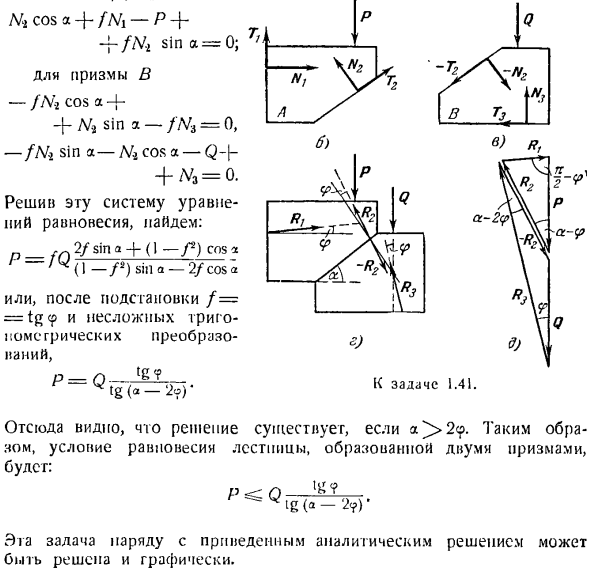
Задача 1.34. Для подъема или спуска по каменному блоку а длиной 2000 ЛГ (рисунок а) использовались 2 клинья В и С. Коэффициент трения контактных поверхностей AB и AC равен / = 0,2, а поверхностей BO и CO/, = = 0,25. К задаче 1.34. Найти равное горизонтальное усилие Р, необходимое для подъема блока а, сжатия клиньев. Определите усилие Р, необходимое для опускания блока а, растягивания клиньев. Решение. Рассмотрим равновесие системы объектов, состоящей из блоков А и Клина в и С.

При подъеме блока (рисунок а) сила Р сжимает клин. Рассмотрим блочное равновесие и клиповое равновесие отдельно. Теперь, когда вы мысленно отбросили клин, замените эти действия блоками \ год Я… Нормальная реакция N и сила трения F (pnc. c). кроме того, на блок действует известная сила. Вес Q. создайте 2 уравнения равновесия, равные нулю сумме проекций всех сил на оси x и Y. £Fbx = jV2 sin 10° — Д/, sin 10° — f-F * cos 10° — F, cos 10°= 0、 ^ Fky = M {cos 10°+ A / acos 10° — Q-F {sin 10° — sin 10°= 0.

Кроме того, описывается зависимость силы трения от вертикального давления Тогда мы найдем тебя： m = M = 1050 кг, Ft = F% = 210 ЛЧ. Переходим далее к рассмотрению равновесия зажима B (рисунок D). B. £Fkx = — Ni sin 10° — Ft cos 10° — Г+Р= 0、 = sin 10° — N-2 cos 10°= 0. Кроме того, существует зависимость силы трения или вертикального давления

Они действуют на клин: реакция блока, которая разлагается на нормальные составляющие-и сила трения-F. h, активная сила P и ползучая реакция разлагаются на нормальную силу 5 и силу трения T. напишите уравнение равновесия для зажима Людмила Фирмаль

Отсюда, используя ранее найденные значения реакции, находим 5 = 996 ЛЧ, Т-249 кг, Р = HkG. Таким образом, для равновесия системы при подъеме блока получено требуемое граничное значение силы а = 641 К1.Система находится в движении. Определите величину силы Р при спуске блока.

Блок а находится в равновесии под действием активной силы-веса Q, нормальной реакции Клина и A^, а также силы страха F}и F (в этом случае сила трения направлена вверх по наклонной плоскости. Это становится ясно сразу же при рассмотрении равновесия зажима B (так как направление фигуры E / сила P изменяется на диаметрально противоположные силы T и-F2, по сравнению с предыдущим случаем, направление изменяется в противоположном направлении (рисунок D).

Уравнение равновесия для блока а выглядит следующим образом: ZrUx = Форекс, потому что 10°-/ \ г Кос 10° — Щ грех 10° -| — / В, Син 10°= 0、 2Fky = НТ соз 10° + COS в \ 0°+ ф {i0 не грех°+ /*.2sin 10° — Q = 0. Кроме того, зависимость силы трения от вертикального давления задается уравнением Я найду тебя отсюда.： L /, = L ’ 4 = 980 кг, = 196 кг.

Уравнение равновесия клина B (рисунок E) выглядит следующим образом: fkx-потому что в I) о _ / В. З / П 10°-Р = 0、 2Fky = S-L / * cos 10° — Г * sin 10°=0.Сила трения выражается вертикальным давлением. Т:=/,$. Отсюда мы находим » используя значения ранее найденных реакций A ^и G. £ = 999 кг, Т-250 ЛГ, П = 273 ЛГ. Найденное значение I является граничным значением при равновесии системы, когда блок опускается.

Итак, на основании проведенного исследования можно сделать вывод, что система находится в равновесном состоянии, если Проекция Силы P находится в следующем диапазоне: −273 кг ^ РХ 641 кф. Если модуль каждой силы Р превышает 641 кг, то ее направление показано на Рис. 5.Теперь, блок будет rise. In для того чтобы блоки начали падать, необходимо приложить усилие Р в противоположном направлении, а их модули должны превышать 273 кг.

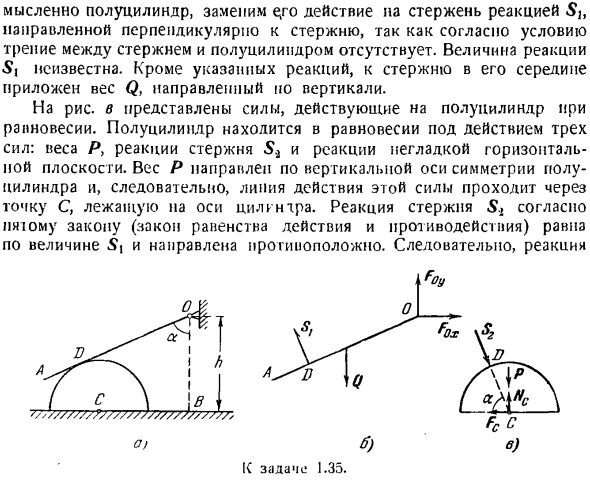
Задача 1.35.Полукруглые колонны веса P и радиуса R расположены на негладкой горизонтальной плоскости(рис. Равномерный стержень OA длины I и веса Q поворачивается в точке O. It лежит на гладкой поверхности полукруглого цилиндра и образует вертикальную ось OL = / g и угол a. Определяет минимальный коэффициент трения скольжения/между полуцилиндрическим цилиндром и горизонтальным!!

Самолет в состоянии равновесия. Решение. Полукруглый цилиндр и стержень представляют собой твердые системы, находящиеся в состоянии равновесия. Под действием веса штока полуцилиндр начинает смещаться вправо(между полуцилиндром и полом недостаточно трения). для определения требуемого минимального значения коэффициента трения скольжения между полуцилиндром и горизонтальной плоскостью рассмотрим баланс штока и полуцилиндра отдельно.

Полукруглый цилиндр и стержень представляют собой твердые системы, находящиеся в состоянии равновесия. Под действием веса штока полуцилиндр начинает смещаться вправо(между полуцилиндром и полом недостаточно трения). для определения требуемого минимального значения коэффициента трения скольжения между полуцилиндром и горизонтальной плоскостью рассмотрим баланс штока и полуцилиндра отдельно.

Рассматривая равновесие стержня ОА (рисунок Б), мысленно отбросьте шарнир О и замените его действие реакцией. Реакция шарнира приложена к точке O, величина и направление неизвестны. Поэтому представим себе реакцию в виде 2-х компонентов F0x и F0y. «S * перпендикулярно стержню, совпадает с касательной и направлением полукруглого цилиндра, а также по радиусу DC.

Этот радиус образует горизонтальный диаметр и угол a полукруглого цилиндра, так как стороны AO и BO, образующие угол a, перпендикулярны прямой DC и горизонтальному диаметру соответственно. Результат реакции негладкой горизонтальной плоскости следует приложить к точке C.

In дело в том, что полукруглый цилиндр находится в состоянии равновесия под действием 3-х непараллельных сил, находящихся в одном и том же plane. As в результате линии действия всех 3 сил пересекаются в 1 точке. Но силы^и Р пересекаются в точке С. Следовательно, линия действия результирующей негладкой плоской реакции должна проходить через точку С.

перейдем к формулировке уравнений равновесия для тел как силы реакции Nc, так и силы трения Fc. построить сумму проекций всех сил на оси x и y относительно стержня и сделать их равными нулю. F0x-Sxc osa = 0, (1） (2） F0y-Q + Si sin a = 0 Уравнение момента для точки O имеет вид: Вопрос-грех \ * ОД =0.(3） Поскольку компонент реакции соединения O не входит в уравнение момента, точка O выбирается в качестве центра момента.

Таким образом, неизвестная сила S непосредственно получается из последнего уравнения, но только эта сила из уравнений (1)-(3), входящих в систему, идет дальше в уравнение равновесия полукруглого цилиндра. Используя формулу (1)-(2), можно найти неизвестные компоненты реакции соединения F0x, F0y.

Из Формулы(3), используя очевидное равенство ОД COS я = ч-г, грехов,(4） Я все выясню.： О ^ АО ХН / потому что грех _h = М-7м-vwt-грех = вопрос lT7r-:-. (о） 1 ^ 2 * ОД ^ 2(А-Р см)в Перейдем к построению уравнений равновесия для полукруглого цилиндра. Получить 2 уравнения равновесия путем проектирования сил, приложенных вдоль осей координат к полуцилиндру. * С4 коза-Кт = 0,(6） НЦ-грех• — Р =0.(7）

Кроме того, сила трения связана с нормальной реакцией зависимостью ФК = фдж \ ’с■(8） Учитывая уравнение, получаем систему из 4 уравнений (5)-(8) исключить оставшиеся неизвестные из рассматриваемой системы, чтобы найти минимальное значение 4 неизвестных Fc, N0 /коэффициент трения f. получить следующее, введя (6) в уравнение (5) и (8). < Грехов 2, потому что.— fN 0 (9） ^ 4 (A-r sin a) J и v ’

Подставляя (7) вместо (5), получаем следующее: Исключая реакцию Li из полученных формул (9) и (10), она в конечном итоге выглядит следующим образом: потому что А. Ф= , 2 П / 2/1 Г У Это минимальное значение коэффициента трения, при котором полуцилиндр и шток находятся в равновесии.

Из опыта известно, что даже если размер компонента Т изменяется в определенном диапазоне, равновесие организма не нарушается disturbed. As в результате сила трения скольжения, обусловленная формулой (2*), изменяется в этих пределах. Итак, сила трения скольжения в состоянии покоя является составной частью реакции сцепления, возникающей под действием активной силы, которая пытается сдвинуть тело.

Этот компонент реакции направлен в сторону, противоположную возможному движению тела. Так как величина силы трения может изменяться от нуля до определенного предела, в зависимости от величины и направления действующей силы、 Р П Рис. 1.37. Рис. 1.36. Препятствует движению тела. Важность силы трения, обусловленной другими реакциями сцепления, заключается в том, что ее модуль не может превышать определенных пределов.

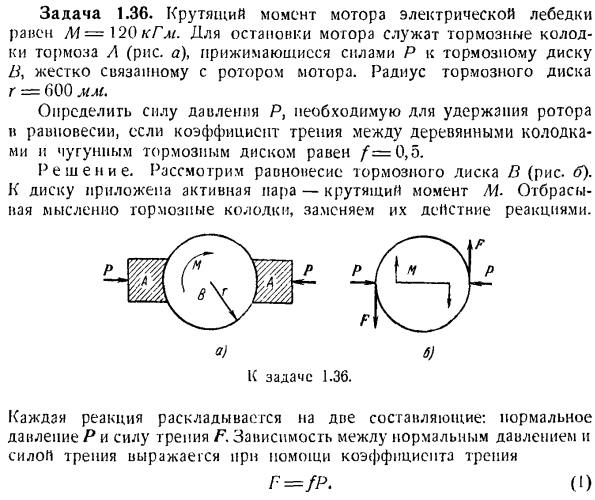
Соотношение между силой трения и вертикальным давлением определяется законом кулона. Максимальная сила трения скольжения пропорциональна вертикальному давлению объекта на поверхность Задача 1.36.Крутящий момент электродвигателя лебедки составляет M = 120 kgm. To остановите двигатель, используя тормозные колодки на тормозе а(рисунок а).

он прижимается силой р к тормозному диску Ву, который плотно соединен с Ротором двигателя. Радиус тормозного диска равен g = 600 мм. Если коэффициент трения между деревянным блоком и чугунным тормозным диском равен/ = 0,5, определите давление Р, необходимое для поддержания Ротора в равновесии. Решение. Рассмотрим равновесие тормозного диска B(рисунок B).

Активная пара приложена к вращающему моменту диска-М. Мысленно отбросьте тормозные колодки и замените их действия реакциями. (Да б.） К задаче 1.36. Каждая реакция распадается на 2 составляющие: вертикальное давление P и силу трения F. соотношение между вертикальным давлением и силой трения выражается с помощью коэффициента трения. Г = / П.

Для равновесия диска необходимо, чтобы сумма моментов всех сил, приложенных к диску, была равна нулю. Сила P уравновешена друг с другом и не входит в уравнение момента. Сила трения образует пару сил. Крутящий момент-это тоже некоторая сила.

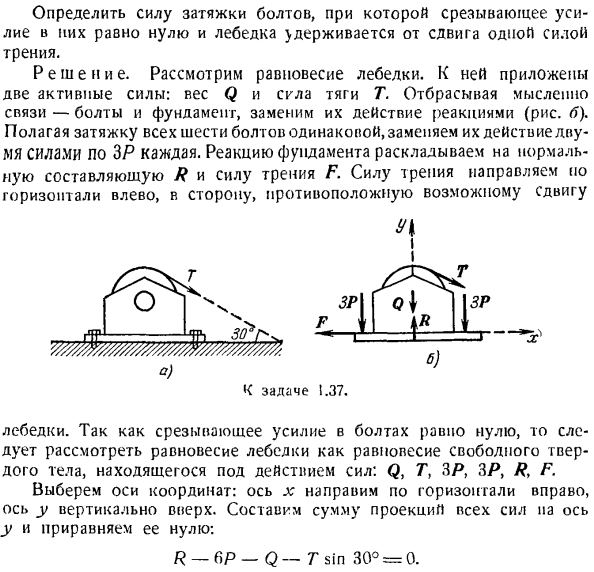
Сумма моментов силы, составляющих пару для любой точки, равна моменту этой пары. Подобный этому R.’2g-M = 0. Подставляя значение силы трения(1)в Формулу(2), получаем: ФП•2р-АФ = 0、 М _ _ _ 120 2г / 2-0. 6 / 0.5- 01 здесь П. С. = 200 кг. Вызов. 1.37. Q = 2T вес электрической лебедки (рисунок а) крепится к фундаменту с помощью 6 болтов.

Максимальная тяговая сила Т составляет 8 т, направленная под углом 30°по отношению к горизонтали. Коэффициент трения между аксонами и основанием лебедки равен / = 0,5. Определяет усилие зажима болта, которое гарантирует, что усилие сдвига Болта равно нулю и что лебедка не срезается силой трения 1. Решение.

Рассмотрим баланс лебедки. 2 прилагается активная сила: вес Q и тяга T. мысленно отбрасывая связи-болты и фундамент, мы заменяем эти действия противодействующей силой (рис. Б). Предположим, что все 6 болтов одинаковы, и замените их на 2 усилия, соответственно, без болтов. Реакция основания ставится на основе нормальной составляющей R и силы трения F. н. К задаче 1.37. Лебедка.

Так как сила сдвига Болта равна нулю, то необходимо рассматривать равновесие лебедки под действием силы как свободное жесткое равновесие: Q, T} 3P, 3P> /?Ф. Выберите ось. ось X ориентирована горизонтально вправо, а ось Y-вертикально вверх. построим сумму проекций всех сил от оси y и сделаем ее равной нулю. Р-6р-Д-Т греха 30°= 0 Из этого уравнения определяется нормальная составляющая основной реакции.

Это будет равняться нормальному давлению и величине фундамента. R = 6P + Q — | — Гsin 30°==6Р-f 2-J-8-0,5 =6Р+ 6.(1） если мы сделаем сумму проекций всех сил на ось x равной нулю, то: Г потому что 30е-ф = 0. Из этого уравнения определяется сила трения, необходимая для достижения равновесия F = Tcos = 6.92 T.(2） Соотношение между силой трения и вертикальным давлением определяется по формуле Я:== / Р

Подставляя значения силы трения(2), вертикального давления(1) и коэффициента трения в эту формулу, получаем: 6.92 =(6р + б) ф =(6р + 6) 0.5、 Где определить затяжку болта требуется (1.92-б.0.5. П = 1.3 т. 6. 0,5. Поэтому необходимо и достаточно, чтобы затяжка каждого болта отвечала условиям так, чтобы болт не подвергался сдвигающему усилию и лебедка была защищена от трения ножницами П ^ 1.3 Т.

Задача 1.38. Q (рисунок L) вес однородного прямого стержня AB находится в точке B грубой вертикальной стенки. Коэффициент трения между стержнем и стеной равен/.в точке а стержень расположен на горизонтальном и гладком полу. Стержень удерживается в равновесии нитью AD, которая перебрасывается через блок D. Минут. б.） Максимальный. К задаче 1.38.

Определите пределы, с помощью которых можно изменять величину нагрузки G, чтобы не нарушать равновесие стержня. Решение. Рассмотрим равновесие стержня AB. 1 на стержень Q действует активная сила, приложенная в точке C к центру стержня C и направленная вниз по вертикали.

Па стержень накладывается 3 скрепления: горизонтальный пол, вертикальная стена и резьба AD. Исходя из закона иммунитета связи, мысленно отбросьте связь и замените действие реакцией. Гладкая реакция Na iol направлена перпендикулярно полу, а натяжение нити P направлено горизонтально вправо.

Реакция грубой вертикальной стенки представлена 2 компонентами: нормальной реакцией Nfl, направленной горизонтально влево, с силой трения Fn. Сила трения направлена перпендикулярно: I) нагрузка P минимальна, следовательно, если возможное направление точки вниз, то сила трения Fn направлена вверх (рис. Б), в направлении, противоположном возможному движению.

2) если нагрузка P имеет максимальную величину, то точка B может начать скольжение ступенькой вверх, поэтому сила трения Fn(рисунок 0) направлена вертикально вниз и снова в противоположном направлении к возможному движению. Если рассматривать равновесие стержня AB под действием 5 сил (Q, NA, Nn, Fn, Ptin (рисунок B)) как свободное твердое тело, то найдем минимальное значение веса груза Pt.

Оси-выберите ось l. направьте ось y вертикально вверх. Создайте уравнение равновесия(рисунок B）： С = Ppiin — = О、 2Ф> г = НС + ФН-Щ = о £(ФК)= ПМ | П и грех-Ф М * 0.5 я потому что-на меня потому что = 0. I последнего уравнения указывает длину стержня AB. In кроме того, описывается зависимость силы трения от вертикального давления ФВ = Т Эта задача определяется статически.

Система из 4 уравнений содержит 4 неизвестных, L’D, Fw, L^, P, nin, поэтому если вы решите систему этого уравнения вместе, то найдете минимальное значение нагрузки P. о р — Минут-tixga + Ф）- Для определения максимального значения нагрузки P рассмотрим равновесие стержня AB (рисунок C) как свободного твердого тела под действием 5 сил: Nn> Flv Q, NA, Ptx. Уравнение равновесия тогда принимает вид £Ф: ВХ = Yashakh-а ’= 0,^ Fhy = на—СГ-г = 0,х(ФК)= Ptrx1 грех м * 0.5 / потому что А-нал, потому что а = 0、 Кроме очага. При решении этой системы уравнений можно увидеть максимальное значение нагрузки P, при котором стержень находится в равновесии.

Из Формулы(I) следует, что в случае tga -/, Rn, ax увеличивается неограниченно. на ТГА необходимо направить силу Q вверх, чтобы поднять стержень (//сдвинуть точку на стене), но это невозможно. Поэтому в этом случае нет силы RTlx, которая могла бы нарушить баланс лестницы. Таким образом, балансировка штанги возможна за счет изменения веса груза P.

−2(ЛАГ — | — / г 1 ′ Эту проблему можно решить несколько иным способом. Заметим, что нет необходимости определять неизвестную силу реакции гладкого пола NA по условиям problem. So, из уравнения равновесия рассматриваемого стержня (рисунок Б) выберите уравнение, не содержащее NA, а затем создайте уравнение момента для всех сил, связанных с точкой А. ВМА(ФК)= НХЛ грех а-j — / ycos а-м ’ — коза = 0.(3）

2-е уравнение равновесия является уравнением проективного итога для пули. Все силы l * на горизонтальной оси. Неизвестная сила L \не входит в него： 1 Fkx =Р» » — Л’й=о. (4） К этим 2 уравнениям добавляется отношение между перпендикулярной реактивной силой и силой трения в точке B\ = ФН РБ, (о） Назначьте значение/ /из (3) в (3) и, учитывая (4), получите его немедленно.

Аналогично, чтобы найти максимальное значение силы P, создайте такое же уравнение равновесия (рисунок C). В та (ф.)=Д? НЛ синий-1:У1 коза-Щ ^ коза=О、 в / — 4jr = Рина, — Л/. = 0,/ — » — Ми- После определения системы уравнений совместно определите максимальное значение силы P. = = −2 ^ JG а-й -•(?） Поэтому, как и ожидалось, результат был выражен в Формуле (2).

Если сравнить оба решения, то можно увидеть, что в первом случае применялся общий метод составления следующего уравнения равновесия. Сила трения всегда направлена в противоположном направлении к возможному относительному движению. Постоянная/называется трением скольжения coefficient. It экспериментально установлено, что этот коэффициент зависит от материала контакта и его шероховатости (чистоты обработки)

.Для абсолютно гладкого тела коэффициент/равен пуле. Реальное тело /> 0. (4 ） Коэффициент трения » не зависит от нормального давления и площади контакта). * ) Недавно экспериментально было установлено, что при изменении нормального давления и площади контакта коэффициент трения изменяется незначительно. Игнорируйте это изменение.

Не принимая во внимание особенности этой проблемы, организм обнаруживает йод под действием какой-либо плоской силы. Преимущество популярных методов заключается в том, что они ведут к цели, несмотря на разницу в условиях выполнения задачи. Иногда этот путь оказывается не самым простым и коротким.

На примере 2-го решения можно увидеть, что, учитывая особенности этой задачи(задача не требует определения уровня реакции L’l на гладком полу), нам удалось сократить число уравнений равновесия, которые проще и с большей вероятностью приведут к песне. Задача 1.39. К каждому соединены 2 одинаковых однородных стержня AB и BC, длина которых равна P/вес каждого other.

In эструс A, стержень AB поворачивается в вертикальную ступеньку. К задаче 1.39.Пятно A находится на высоте h над уровнем пола, и там бар BC устанавливается в конце C по желанию. Зная коэффициент трения между стержнем летательного аппарата и горизонтальным полом, определите угол£в состоянии равновесия.

Решение. Рассмотрим отдельно баланс стержней BC (рисунок B) и AB (рисунок C).Теперь, когда вы мысленно отбросили эту связь, замените эти действия реакциями. К стержню БК прилагаются следующие силы: масса Р, нормальная реактивная сила горизонтального пола N и сила трения F, направленная в противоположном направлении к возможному движению.

Реакция шарпии B неизвестна по размеру и направлению(обозначается 2 компонентами SBx и Sr {y). К стержню AB приложены следующие силы: масса реакционной составляющей соединения B, P1, равна силе, приложенной к стержню BC в точке B, и противоположна(обозначая эти компоненты S & *и 5^ -).

Компоненты реакции соединения а, называемые RAx и RAy. Составьте уравнение экстремального равновесия ядра летательного аппарата. Г — = О、 (1） (2） (3） / ФЛ грех? — N1 cos E + P fj cos J = O、 Уравнение момента (3)суммируется относительно точки B, а уравнение (4)дает зависимость силы трения от вертикального давления. Уравнение равновесия для стержня A / 3 выглядит следующим образом: Shx-RAx = 0, (5）

Застенчивый-П + Рей = ВЗ(6） Skxt sin a-S’N YL cos a-j-P Ty cos a = 0 (7） Здесь сумма моментов силы(7) производится относительно точки А. Чтобы найти уравнение, определяющее связь между углами a и p, решите уравнение, состоящее из Совместного исключения уравнений (5) и (b).Из уравнений (I), (2) и (4) можно увидеть следующее: Технологии SBX = F(Р + Snvy(8）

Если убрать неизвестные P, N из уравнения(3), то это выглядит так: Snx по / грех 3-(П-Джей — SIiy) я что? + С потому что? =0.(9） Если разделить это равенство na / cos J3 и использовать равенство(8), то можно увидеть следующее: F(Р + сны) тг? -с» г—j =0 и.(10） С другой стороны, если разделить уравнение (7) на/ cos a и использовать уравнение (8), то получится: F(Р + SnJb * — СБ> + т = а Исключить из уравнения (10)и (11) Sny?

Я все выясню.： ; Hg (3-tg (\2） Это первое уравнение, определяющее угол i, p в положении равновесия. Найти 2-е уравнение из геометрического уравнения Я грешу 3-П / Син А = А,(13） Где я могу его достать： грех п-ф-грех = г (14） При исключении угла а из равенства(12)и(14)、 Извините. Если Po является корнем этого уравнения, то равновесие системы будет в случае p> p0.

Задача 1.40.Однородный стержень длины / AB опирается на гладкую поверхность ребром A внутри полого полукруглого цилиндра радиуса r и ребром B на шероховатом горизонтальном полу (/<[2r). в положении равновесия центр тяжести стержня C находится выше вертикального диаметра полукруглого цилиндра.

Предполагая, что сила трения достигает этого положения, определите угол Р стержня, когда пол находится в уравновешенном положении, а также коэффициент трения между стержнем и полом и скольжение/. К задаче 1.40. ПИИ стержень своей конечной ценности. Решение.

Рассмотрим равновесие стержня AB. 1. одна активная сила действует на вес штока P. Так как центр тяжести штока C находится на той же вертикальной линии, что и центр цилиндра O, то линия действия силы тяжести проходит через точку O. На стержнях были уложены 2 скрепления: гладкая поверхность полукруглого цилиндра и шероховатый пол.

Мы будем применять закон, который освобождает от отношений. Мысленно отбросьте связь(рисунок Б) и замените действие реакцией. Реакция гладких стенок полукруглого цилиндра обычно направлена на его поверхность, то есть вдоль радиуса АО. Давайте выразим это с силой T. As в результате линия действия 2 сил пересечется в точке O. реакция T и масса P. линия действия реакции R iol также должна пересечь точку O. укажите реакцию R, а не реакцию BO(рисунок b).

Угол между нормалью пола и реакцией R является углом трения, и вы можете увидеть следующее из треугольника / = tg OBD. и… Би), БЦ, потому что 3 / соѕ? / ВНУТРИВЕННЫЙ Буква А обозначает угол между силой Т и горизонтом.

Затем, если вы отбросите вертикаль AN из точки A в вертикальный диаметр, LL / = = AO cos a = AC cos%или Р соѕ а = ^ п, потому что. (2） Аналогично, ON = r sin 1 и DN = t sin [3; следовательно、 Грех т а-j — / грех р = р. Сравнивая (1) и(2), можно увидеть следующее: потому что А = Ф. (4） Для краткости — = b <I (согласно гипотезе f <2r), из(2)и(3 коза =£cosJ3,(5） sin a = от 1 до 26 секунд

И значением функции COS в точке 3 становится мнимым в эго. Итак, наконец-то потому что. 8 =〜）/ 3 * ’-2 + Y 4-3b \ Ф = Б, потому что Е = ^ \ / Т М *-2 в 4-СР> *. Решение этой задачи отличается от большинства задач равновесия при наличии трения тем, что оно не разлагает реакцию шероховатой поверхности на нормальные составляющие и силы трения. Задача 1.4! 2 одинаковые призмы A и B образуют лестницу.

Шаги нагружены силами P и Q, и показаны точки их приложения(рисунок O).Призма а расположена на вертикальной стенке, а плоскостью 2-й призмы мы наклоняем йод под углом а. призма Б расположена на горизонтальном полу. Определите равновесное состояние, учитывая трение всех контактных поверхностей.

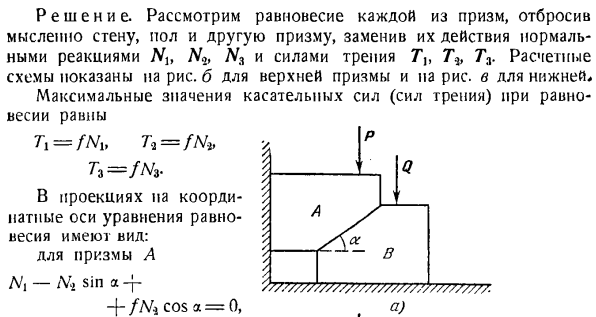
Коэффициент трения горизонтального пола, вертикальной стенки и призмы друг о друга одинаков, а f = tg’F равен them. In по сравнению с силой P и Q, собственный вес призмы пренебрежимо мал. Решение. Рассматривая равновесие каждой призмы, мысленно отбрасываем стены, пол и другую призму, заменяя их действия обычными реактивными Nh No, N3 и силой трения Titmu*Т.

Схема конструкции показана на рисунке. B Верхняя призма и ПА figure. At на дне. Максимальное значение тангенциальной силы (силы трения) в равновесном состоянии составляет ТХ = / М, Т = ФН * Т%= / Л / С П. С. Q. В проекции координатная ось уравнения равновесия имеет рейку: Призма а / 777777Z777777777777777777777777777777. / Л / — Л4 грех-Джей- + / Л / я COS я = о、 Макоса+ / М-П + — Ф / М Син А==: 0; 3 / ’ Для Призмы B — ФН \ потому что а-j- + Ни грех-комплексы FN6 = 0、 — фни грех-ни потому что- + / В3 = 0.

После решения этой системы уравнений равновесия, мы видим, что: П-10 2 / грех г-ч 1-я потому что ’(1 — / 2) зта-2 / потому что Или / — = tg и после подстановки простого тригонометрического преобразования、 ВТГ(а-2О) ’ Q. \ — ТУ Х»? 1%б％\ c)я д.） К задаче 1.41. Это означает, что для a> 2

2 вертикальная сила реакции гладкой плоскости на вертикальной силы реакции Призма НН, тангенциальная сила реакции призму ТБ (сила трения). Создайте уравнение момента для точки А. — О• -!Cosт Р.- Джей, В » • = О、 ’1 «sim 1 < 7 / Где я могу его достать： 1А.

НОТАБЕНЕ. = Н потому что это-грех. Подумайте далее о предельном равновесии призмы и мысленно отбросьте пол и стержень. На призму воздействуют (рисунок с): Масса Q, давление стержня-Nti, сила трения-нормальная реакция плоскостей Tb и N0. Где должна быть связана нормальная реакционная плоскость результата?

С правой стороны силы Q, сила Q не может быть применена. Потому что относительно такой точки не удовлетворяется, что она равна нулю суммы всех сил моментов. Поэтому точка приложения реакции находится в левой половине сегмента OE. Его крайнее положение, которое соответствует критическому равновесию в точке О, когда призма может начать вращаться вокруг ребра bones. So …

И получаем ранее найденное значение, и предыдущее уравнение. GI.01•/-> Б Л в ■ ТГ СР * потому что, потому что грех есть * ведь * грех * грехМ ^ = 0. ЭДД. Вопрос.= — (тг 9 потому что это-грех), потому что грех = Я… = «Тг — — — — (9 потому что-cosФsin а)•грех 2а、 потому что ф т Я найду тебя отсюда.： Е <б =- < P Или в конце М = н-грех (φ-а) грех 2а. −26 соѕ СР ВР 7

Из этого уравнения мы также можем видеть, что существует решение проблемы. В противном случае, потому что вес призмы оказывается отрицательным、 Это невозможно. Чем ближе угол наклона стержня к углу трения, тем легче призма. при a = cp даже невесомая призма остается сбалансированной. Задача 1.43.

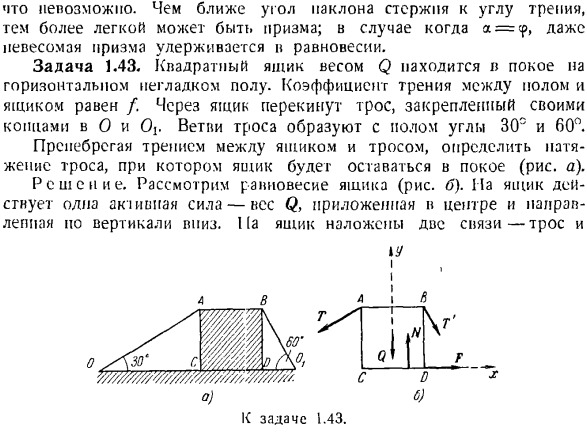
Квадратная коробка весом Q расположена на негоризонтальном гладком полу. Коэффициент трения между полом и коробкой равен/.Пропустите кабель через коробку и закрепите концы к О. ветвь кабеля образует угол 30°и 60°с ИОЛ. Не обращая внимания на трение между коробкой и кабелем, определите натяжение кабеля, при котором коробка останется неподвижной (рисунок а). Решение. Рассмотрим баланс коробки(рисунок B). Коробка па контролирует 1 силу удара Аю-вес Q. It наносится на середину, вертикально, но вниз. 1(и есть 2 ссылки в коробке-кабель и \ У К задаче 1.43.

Секс мысленно разрушает эти связи и заменяет их реакцию. Потому что никакое трение между коробкой и кабелем, напряжение кабеля т будет этим же везде. Натяжение кабеля действует на коробку в направлении OA и OhV (рисунок A).Разберите реакцию пола на обычную реакцию N силой трения и касательную реакцию F. Рассмотрим равновесие коробки как свободного тела, в котором находится йод, под действием 5 сил, показанных на рисунке. Составьте уравнение баланса и сделайте пулю равной сумме проекций всех сил на ось хны. (1） (2） (3） (4）

Потому что Т-60 »- т соѕ 30° — ф-ф = 0, П-М-Т грех GO1 ′ — ’ / Син 30°= 0. Кроме того, существует связь между силой трения и нормальным давлением (по модулю равным нормальной силе реакции), то есть： Ф = ФН. (2) от：。 N = Q-f-7(sin 00° — f sin 30°). Если мы присвоим это значение (3), а затем (I), то получим: 7 (cos 60° — cos 30°)+ / [_ / 0 _ 2 / В. cos30e-потому что 60°-/(греха 60′ — sin30e)| /з_ _ я(Дж / 3 Коробка. .. т ^ по качеству звука ^ Ю. Г.-Я-/(КЗ +1）

Задача 1.44.2 цилиндры с радиусами r и r}и грузами P и P2 представляют собой прямые линии, соединяющие центр цилиндра 0j0.JF размещается на горизонтальных стойках и вертикальных стенах таким образом, чтобы образовывать угол r и угол cp. К задаче 1.44. С зонтиком.Коэффициент трения: между первым цилиндром и горизонтальным полом/, между вторым цилиндром и вертикальной стенкой / 2 и между цилиндром/.

Определите минимум этих коэффициентов, чтобы система могла находиться в равновесии, и нормальную реакцию реакции между Иолой, ступенью и цилиндром. Решение.Рассмотрим равновесие каждого цилиндра отдельно (рис. Б и в \пол, ступень и другие цилиндры мысленно разрушаются, заменяя их действие реакцией.Разбейте каждую реакцию на нормальные компоненты и силы трения.После этого первый цилиндр подвергается уравновешиванию под действием 5 сил: веса, 2 сил вертикальной реакции, 2 сил трения (рисунок б).

Учитывается также равновесие 2-го цилиндра (рисунок с).Сила трения направлена по касательной, проведенной к цилиндру в точке соприкосновения.Система может использоваться для перемещения цилиндров и встречных цилиндров. Создайте уравнение равновесия первого цилиндра:>] Fkx = FX-n cos 9 F sin 9-0, X Fky = Ni-P, — N sin 9-F cos 9 = 0、 2 F^, — = 0.

Уравнение равновесия 2-го цилиндра выглядит следующим образом: 2] Fhx = n cos 9-Ni-F sin 9 = 0,£Fky = N sin 9-P-2 + F-2 + F cos 9 = 0, I mo2 C7) = — Fr,= 0. (О (2） Добавьте к этим уравнениям равновесия зависимость предельного давления от вертикального давления Ф = ФН、 В результате совместного решения системы из 9 уравнений (I)-(3) мы нашли: (3） РА с COS <Р «Пи(я + грех <Р4-потому что» п) — (- па (я + sin9） L = 1; потому что о 1 грех 9 * 1 ’1 H-sin<f-p COS <P м.__ = / Vi 1 4-sill cp + cos <p’y-G » Потому что? ’

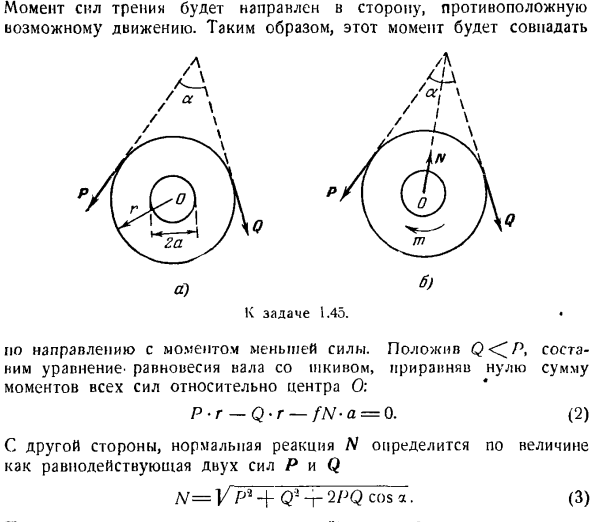
Полученное значение коэффициента трения является минимальным. При превышении этих значений равновесие системы сохраняется, а сила трения не достигает предельного значения. Задача 1.45.Шкив радиуса r прикреплен к валу радиуса a, который может вращаться внутри подшипника. Коэффициент трения между валом и подшипником.

Усилие Q прикладывается к шкиву для определения максимального значения силы P, удерживающей шкив в неподвижном состоянии, когда он образует силу P и угол a (рисунок A). найти значение силы P, если n = k / 2 и если силы P и Q параллельны. Решение. Мысленно отбросив подшипник, мы учитываем равновесие со шкивом вала и заменяем действие подшипника обычной реакцией N и силой трения t. момент силы трения (относительно точки O) равен、 0.） м = / н.

Если проецировать все силы горизонтально, то можно увидеть: Q sin a-F = 0 или Qsina-F. (7 *） Максимальная сила трения Fмакс = = / Г Я,(8 *） А ТГА <^ тг?Рассмотрим следующий вывод. М $ Ина ） Так, сила Q, линия действия которой находится внутри конуса трения, не может сдвинуть тело с места, каким бы большим ни был объект.Некоторые автоматические тормозные устройства основаны на этом свойстве. Если вы выберете вес P из 0, неравенство (9) будет Ци грех 1

Если на стадии рассмотрения Знак минус знака равенства(7)соответствует Q ^> P, где момент трения совпадает с моментом силы P. Для овладения навыком решения задачи равновесия при наличии трения скольжения можно использовать I.V.It рекомендуется решить следующие задачи из сборника теоретической механики и задач Бол в 1950 г. Ме-Терского.Более поздние годы：67、71、73、74、174、175、170、177、178、180、181、180、187 2°.

Равновесие твердых тел при наличии трения качения.Между роликом и плоскостью, на которой размещен ролик, к оси зубцов прикладывается сила»S» (рис.1.42), и создается сила трения, которая стремится переместить ролик на плоскость.Рассмотрим случай, когда Сила 5 параллельна горизонтальной плоскости. Из опыта известно, что при изменении величины нулевой силы S до определенного предела 5 GF ролики остаются неподвижными, то есть сила, действующая на ролики, равна balanced.

In дополнение к активной силе: вес P и сила S, плоская реактивная сила к ролику приложены и свое равновесие учтено.Поскольку остальные 2 силы приложены к этой точке, из состояния равновесия 3 непараллельных сил следует, что реакция R-плоскости должна проходить через центр ролика O. Поэтому точка приложения реакции С должна быть смещена на расстояние/ к от вертикали, проходящей через череп к центру колеса.

Если нет, то реакция R не будет горизонтальной. Рис. 1.42. Это необходимо для соблюдения условий равновесия. ■ Реакция R-плоскости разлагается на 2 компонента.Нормальной составляющей N является касательная реакция F, представляющая собой силу трения(рис. 1.43). Так, при крайнем положении равновесия звена применяются 2 взаимно уравновешенные пары: 1-я пара сил (5, F) момента Snp-r (R-радиус звена) и 2-я пара сил (N, I), удерживающих звено.2-я пара моментов, называемая моментом трения качения, является ММН = ФКН (12 *）

Где/ k-коэффициент трения качения, измеренный в единицах длины.Этот коэффициент можно рассматривать как расстояние, на котором отдача N перемещается от вертикали через центр ролика. Для получения чистого качения (без скольжения) сила трения F должна быть меньше максимальной силы скольжения. Ф <ФН(13 *）

Где / — коэффициент трения скольжения. Трение качения возникает из-за деформации ролика и плоскости, в результате чего происходит » контакт между роликом и плоскостью SH777Sh Sh7777777） Рис. 1.43. Происходит на одной стороне ролика, на смешивая пункте или на дне, в направлении возможного movement.To для решения задачи о равновесии твердых тел при наличии трения качения необходимо выполнить первые 4 пункта.

Нормаль, проведенная от центра ледяного звена, проходит через пересечение O других 2 сил, действующих на ледяное звено (рис. 1.42） 5) сравните число неизвестных и число уравнений равновесия и добавьте к ним зависимость вертикального давления от момента трения.Если задача определяется статически,то число неизвестных должно быть равно числу уравнений. 6) комп

Задача 1.46.Цилиндрические ролики диаметром 60 см и массой Q = 392 кг совершаются в равномерном движении человеком, который нажимает на рукоятку АО = 1,5 м с определенной силой Р в направлении АО. Высота хомута а от горизонтальной проезжей части составляет 1,2 м, а коэффициент трения качения ролика составляет / = 0,5 см.

Определить величину силы Р, силы трения при качении, нормальной составляющей реакции в горизонтальной плоскости (рисунок а).Коэффициент трения скольжения между роликом и дорогой/ = 0,2. Решение. Если ролики вращаются равномерно, то все силы, действующие на ролики, уравновешиваются.

На звено воздействуют 2 активные силы: вес звена Q и давление человека R. 1 звено прикладывается к кардоку (горизонтальной плоскости). применяя закон освобождения! И, от связи, мысленно опустил горизонтальную плоскость、 Асисуп. б.） К выпуску 1.46. Замените реакцию на R.

Эта реакция применяется к точке C, которая находится на расстоянии/ k от вертикальной линии, проходящей через центр колеса. Согласно теореме о 3 непараллельных силах, в случае равновесия его рабочая линия пересекается в 1 точке О, так что не действующая R направлена вдоль прямой(рис. Б).

Реакция плоскости R разлагается на 2 составляющие. Нормальная составляющая n перпендикулярна плоскости, а тангенциальная составляющая, ориентированная вдоль плоскости,-силе трения G при прокатке. Под действием 4 сил: Q, P, N, F, рассмотрим равновесие винтиков как твердого тела. Выберите декартову систему координат. ось X направлена горизонтально вправо, а ось Y направлена вертикально вверх через центр ролика.

Создайте уравнение равновесия. Если отметить угол между горизонталью (осью jc)и ручкой ОЛ буквой A, то он выглядит так: В уравнении(3), буква R обозначает радиус ролика. Суммируя сумму моментов сил, связанных с точкой C, сила I, приложенная к центру ролика O, разлагается на 2 составляющие: горизонтальную (P cos a) и вертикальную (P sin a), и теорема Варигноупа имеет вид used.

In кроме того, как правило, при расчете момента горизонтальной составляющей силы Р мы пренебрегаем изменением ее плеча, считая, что оно равно радиусу ролика R. найти величину искомой силы Р можно по формуле(3)： р = р в *. = 392 ^ 5osecose— /ksina1. 2 0.9 175 г ^ с Равенство (2) обеспечивает: Н = М + П грех = 392 + 8.27 у = 396.95 г Из Формулы (1) определите величину силы трения. Ф = Р потому что — = 8.27 б? = с, 63 кг.

Сравним силу трения F при качении со значением силы трения скольжения и посмотрим, происходит ли в этом случае чистое качение или происходит скольжение. Сила трения скольжения Ft = / L’ — 0,2•396,95 = 79,4 кг. Таким образом, сила трения скольжения * больше силы трения качения. 、 Интернет> Ф Каток будет катиться без скольжения.

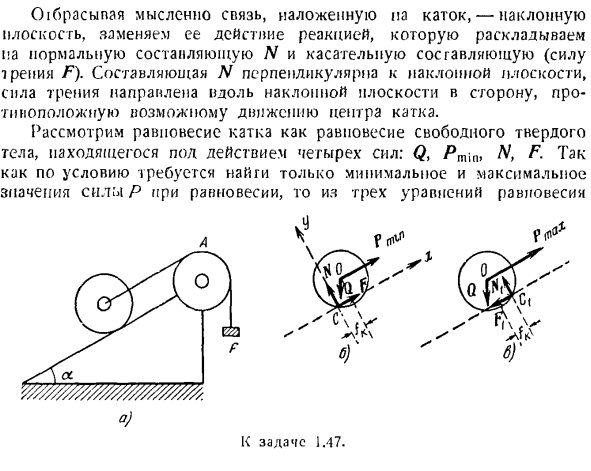
Задача 1.47.Цилиндрический ролик с радиусом r и весом Q (рис. а) уравновешивается наклонной плоскостью, которая образует угол а с горизонтальной линией резьбы, перекинутой через блок А. груз весом Р опускается до конца резьбы. Коэффициент трения качения ролика равен/ к.

Определите минимальное и максимальное значения веса Р, при котором ролик будет находиться в состоянии равновесия. Найти минимальное значение коэффициента трения скольжения/. в случае движения ролики будут катиться без скольжения. Решение. Рассмотрим баланс ссылок в 2 случаях. В первом случае, если величина Р является минимальной величиной, то возможное направление движения ролика находится на наклонной плоскости (рис. 1). в этом случае точка С, к которой приложена плоскость противодействия, перемешивается на расстоянии/ к слева от вертикали, до точки полового созревания от центра ролика о до наклонной плоскости.

На крючок прикладывается 2 активных усилия: вес Q и натяжение нити Pmin. Таким образом, сила Q не может нарушить равновесие организма. Сила трения может принять пулю к другому значению или максимуму. Таким образом, уравнение (§ 2, уравнение (Г*）、（2 *）、（3 *）|）уравнение равновесия твердого тела, представленное неравенством, если существует сила трения.

Найти максимальное значение силы трения и найти предельное значение (максимальное и минимальное) величины, которое можно получить из уравнения равновесия. Так, например, принимая во внимание равновесие лестницы АВ (рис. 1.41), прислонитесь к гладкой ступеньке и неровному полу, приняв максимум силы трения, и вы найдете минимум угла а, под которым лестница будет находиться stationary. I

n в этом случае положение равновесия бесконечно велико. Если значение угла а найдено, то не менее 90°, так как для равновесия требуется сила трения меньше максимальной. При решении задач о равновесии твердого тела с силой и степенью силы трения).41. первые 4 точки, указанные в начале n и g, должны быть заполнены (стр. 15). в этом случае реакция шероховатой поверхности должна быть выражена в 2 компонентах. Нормальная реакция и сила трения, или трение 9 к поверхности нормальное (с максимальной силой трения）;

(Соединение накладывают на ролик, мысленно отбрасывая наклонную плоскость, заменяя ее действие противодействием. Это распространяется на нормальную составляющую N и касательную составляющую (силу трения F).Компонент N перпендикулярен наклонной плоскости, а сила трения направлена в противоположную сторону вдоль наклонной плоскости возможного перемещения центра ролика. Равновесие ролика

считается равновесием свободных тел под действием 4 сил (Q, / V, n, N, F).Из 3 уравнений равновесия, поскольку по условиям необходимо найти только минимум и максимум силы P при равновесии К задаче 1.47. Составьте 1 уравнение, представляющее собой равенство суммы моментов всех сил, связанных с точкой с, нулю. С ТК(FН)= — fKQ потому что-(в грех-ПМ] х)р = 0 (я） Это уравнение не содержит неизвестных сил N и F}.Потому что они применяются в точке С. При создании уравнения мы разложили силу QPA на 2 составляющие: Q cos ((плечо этой составляющей к точке C равно коэффициенту трения качения/ k) направлено перпендикулярно нак

лонной плоскости, а составляющая Q sin a направлена параллельно наклонной плоскости и в сторону от нее. Если решить уравнение (1) относительно RT, то получим: (2） Теперь рассмотрим 2-й случай, когда сила P достигает максимального значения, при котором равновесие possible. In в этом случае возможное направление ролика направлено вверх по наклонной плоскости (рисунок I).Сила Q и Ht1X направлены, как и в первом случае, а nc добавляется к центру кагка O, как и раньше. На этот раз плоскость прикладывается в точке C и перем

ешивается расстоянием fK вправо вдоль наклонной плоскости. Создайте уравнение момента для точки C. 2 МРП(FН)= АQ потому что-(Р | РС-м зта) Р = 0. / Jmax = м [грех +£коза]. (3） Таким образом, если сила P находится в следующем диапазоне, ролик будет находиться в сбалансированном состоянии на наклонной поверхности. М£греха * потому что J Р ^ вопросы греха, а-j-при COS Дж. Определите минимальное значение коэффициента трения скольжения/.при этом значении, в случае движения, цилиндр не скользит, а катится. Во-первых, рассмотрим случай, когда вес груза P минимален. Пусть пуля приравнена к сумме проекций всех сил на ось x, параллельную наклонной плоскости, и на ось y, перпендикулярную ей(рис. Присвоить первому уравнению 2 fhx по =Анин р-р-м зта = о (2) найти соответствующее P » iin>значение с

илы трения при прокатке F = / kqc os a. g. Второе уравнение равновесия ^ Fky по = Н-м потому что = о Можно определить нормальное давление равное величине нормальной реакции гг = г потому что. Условия, при которых происходит чистое скольжение, следующие: F <Нет(4） Где / — коэффициент трения скольжения. Если ввести значения F и N в (4), то можно увидеть следующее: К / 7 < / (5） Рассмотрим далее случай, когда вес груза P имеет максимальное значение(рис. с). в этом случае проекционное уравнение выглядит следующим образом: £СГ * = — интернет-Qsin а =（ «） ^ Fhy = / V, — Q cos a =0.By вводим значение Ptx (3) в уравнение (6)、 Кфи = у Q соѕ А,/ В, и Q, потому что. Подставляя эти значения в (4), получаем чистое состояние качения Задача 1.48.Стальной цилиндр радиуса r прослоен между 2 параллельными направляющими, и направляющая под ним зафиксирована для того чтобы не д

винуть, и направляющий выступ выше можно двинуть линейно параллельно к первоначально положению. Верхняя направляющая прижимается к диску вертикальной силой Р(рисунок а).Коэффициент трения качения между палиндромом, нижней и верхней направляющими равен| K / соответственно. И / или выше. Не обращая внимания на вес цилиндра и направляющей, найдите максимальное усилие Tm, приложенное к верхней направляющей, где цилиндр останется неподвижным. Решение.

Рассматривая равновесие цилиндра(рисунок Б), мысленно отбросьте нижнюю направляющую и верхнюю направляющую, заменив действие реакцией. Затем нормальная реакция Ai и сила трения 7 \действуют на цилиндр со стороны нижней направляющей, вертикальная сила реакции iV.2 и сила трения T \ 2 действуют со стороны верхней направляющей. guide. In в этом случае точка приложения реакции нижней направляющей переместится вправо от вертикального диаметра на расстояние/, а точка приложения реакции верхней направляющей переместится на расстояние/ Ki влево от вертикального диаметра, т. е. 6.） th.） К задаче 1.48. Возможно перемещение цилиндра по каждой направляющей. С другой стороны, если рассматривать

равновесие между цилиндром и верхней направляющей, проецирующей силу вертикально, то оно выглядит так: А / Дж-П = О или в / О,= Р Далее Вернемся к рассмотрению цилиндра(рис. Б) и проецировать силу вертикально. L’, — iV2 = 0 или N \ N \ =P. далее построим сумму моментов всех сил, связанных с точкой A. Л ’,/ К1-я-П•2г = о、 Наибольшая искомая сила равна Если коэффициент трения качения равен / к (=/кДж = А. И затем… т.-

Для овладения навыками решения задач с равновесием объектов при наличии трения качения необходимо использовать И. В. рекомендуется решать следующие задачи Из «сборника задач теоретической механики» Мещерского.190, 191, 192. 3°.Равновесие твердых тел при трении гибких тел. Предположим, что нить намотана на неподвижный цилиндр, и на одном его конце приложена нагрузка Р. (Рисунок 1. 44).Коэффициент трения резьбы о шероховатую поверхность цилиндр

а равен/.Тогда сила T, необходимая для поддержания нагрузки P в равновесии, определяется по формуле Эйлера. Рис. 1.41. ш Р — А. (14 ） Т = Ре Где E-основание натурального логарифма. Таким образом, сила T для уравновешивания нагрузки P не зависит от R диаметра цилиндра и является функцией угла охвата и коэффициента трения. Для решения задачи о равновесии твердых тел при наличии трения гибких нитей、 Первые 4 пункта перечислены в начале книги. 15.Следующий： 5) сравните число неизвестных величин с числом уравнений равновесия, добавь

те зависимости натяжения нити (14) с обеих сторон покрытых тел к уравнениям равновесия и убедитесь, что число независимых уравнений равно числу! поэтому задача определяется статически. G) выберите систему координат. 7) создайте уравнения равновесия для твердых тел. 8) после решения этой системы уравнений определите неизвестные величины. Задача 1.49

.При швартовке судна матрос нажимает на трос BOC!»Натяжение каната равно Q, а сила, с которой матрос держит канат, равна A. угол крышки каната каждой колонны равен 210°. Определите коэффициент истирания каната для столба, Если вы знаете, что моряки могут применять 3 из 8 для удержания каната. Установите коэффициент трения чугунного колонного каната равным 0,15 = для определения величины натяжения, которое может выдержать матрос при усилии Р = 60 кг. Разрешен и Е. угол охвата. Веревка в 1 ряду равна О Перекрытие 3

8, угол канатного перекрытия столбов составляет 6 раз (7 -*).Тогда зависимость натяжения 2 K Q. Определите минимальное значение коэффициента трения между валом и тросом, при котором груз будет находиться в состоянии равновесия. Найти нагрузку Р, сравнив коэффициент трения троса на валу с/ = 0.25.It может уравновешиваться нагрузкой Q = 10 кг. Решение. Рассмотрим равновесную часть троса, охватывающего левый вал (рис. Так как активная сила R действует на трос, м

ысленно отбрасывая вал с правой стороны, перерезая трос между валами и заменяя действие с правой стороны натяжением троса T. К задаче Мне 50. б.） Чтобы сбалансировать эту часть кабеля, равенство должно быть соблюдено Т = Пе} \± Здесь угол охвата составляет 3/2.Так… T = ПК） Далее, принимая во внимание равновесие правого вала (рисунок 0),

мысленно отбрасываем левый вал, отсоединяя трос и заменяя его действие силой G. согласно закону равенства действия и натяжения реакции T и/’], величины equal. To сбалансируйте части кабеля, которые покрывают правильный вал, равенство должно быть соблюдено Правый вал, а также угол охвата- Если решить уравнения (I) и (2) вместе, то напряжение ipoca между валами T исключается. >> 01 здесь Ф 1, р / => — в-

, и на одном его конце приложена нагрузка Р. (Рисунок 1. 44).Коэффициент трения резьбы о шероховатую поверхность цилиндра равен/.Тогда сила T, необходимая для поддержания нагрузки P в равновесии, определяется по формуле Эйлера. Рис. 1.41. ш Р — А. (14 *） Т = Ре Где E-основание натурального логарифма. Таким образом, сила T для уравновешивания нагрузки P не зависит от R диаметра цилиндра и является функцией угла охвата и коэффициента трения. Для решения

задачи о равновесии твердых тел при наличии трения гибких нитей、 Первые 4 пункта перечислены в начале книги. 15.Следующий： 5) сравните числоТу же проблему можно решить и другим способом. Рассмотрим общее равновесие кабеля(рисунок а), общий угол охвата кабеля 2 валами 3.3 В: у меня *. 2 * = ’ Найдите отношение между силой P и силой Q. Вопрос = ПК ’ ТФИ У нас есть： Для определения величины нагрузки P, которую можно удерживать в равновесии при нагрузке Q = 10 кг, находим следующую формулу из(3): £ — =3и: / = 2.358. И затем… f = 10,5 и P = 10-10. 5 = 105 кг. Таким образом, нагрузка Q 10 кг може

т удерживать нагрузку P 105 кг в равновесии. Задача 1.51.Кабель AB охватывает барабан, вращающийся вокруг центра O. коэффициент трения кабеля о барабан равен/. Обруч кабеля Liv установлен на плохом рычаге и может быть вращан вокруг пункта D. расстояние AI)= a, BD-B. Си. Г в 6 I A X О е.） о.） СЗ. б.） ymq. К выпуску 1.51. Определите натяжение троса в точках А и В. Если вес неисправного рычага проигнорирован, то груз Q под

вешивается к рычагу так, что давление в точке D равно нулю, расстояние CD = C. Решение. Рассмотрим равновесное состояние троса, охватывающего барабан, и мысленно отбросим рычаг (рис. Согласно формуле (и), соотношение между этими напряжениями определяется по формуле: £=(1） Потому что угол кабеля барабанчика tf. (1) индекс является положительным. Потому что, по отношению к предопределенному направлению вра

щения барабана, напряжение^ сидит Далее, в соответствии с условиями задачи, рассмотрим равновесие плохого рычага, предполагая, что давление в точке D, а следовательно и реакция шарнира D, равна нулю. Активная сила Q действует на рычаги. Мысленно отбросьте кабель и замените его действие реакцией 6 \и S&(рисунок C).Очевидно= ^ =, Выберите координатные оси для создания уравнения равновесия == (2) 2 мкр (ФК) = КК-З \ А ’^ Б =0.(3） 3 уравнения с 3 неизвестными S’V S ^ s（1）、（2）、（3）система была получена. Из уравнений (I)и(2) получаем следующ

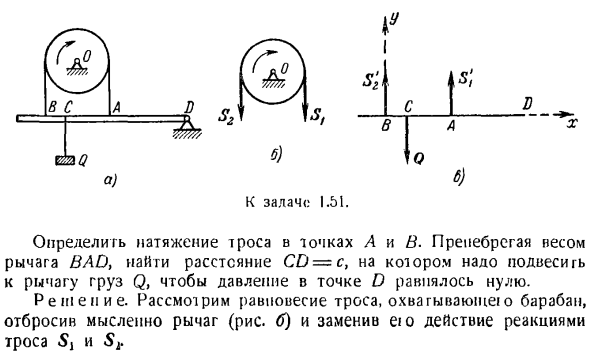
ее: с ’ _ _ О 2Мб (ФК)= С ’ Л, (Б-а) — м(б-с)= 0 Если вы решите эти уравнения с равенством (1), вы получите ответ, полученный ранее. Задача 1.62.As показанный на рисунке 5, пояс навинчен на 5 неподвижных роликов. а. коэффициент трения ремня о ролик/ = 0,4. Расстояние между центрами роликов на 1 прямой составляет / = 50 мм. диаметр ролика d = 25 мм. усил

ие P = 150 кг прикладывается к левой стороне ленты. Каково минимальное значение силы Q, при которой ремень становится рыхлым? Решение. Указывает угол наклона ролика ремня. Затем вы можете описать сегмент ремня, который охватывает каждый из роликов следующим образом: Коэффициент натяжения ремня с обеих сторон ролика： 7 \ = 7В / а、 А =он.、•»•»• 7 \ = РСИ. Если исключить из этой системы уравнений

промежуточную силу 7 * 1, т ^(умножив все уравнения、 Вопрос = ПК ^ а. (1） Углы также равны прямоугольные треугольники АО ^ B и АО.. Определяется из C (рисунок B）： / грех Дж = д、 Откуда? •^®^ Л ы грех 2 = = — = 0,5、 A = 60°= 1.0472 серия. Затем найдите следующее Из(I): М = 150•Р5 0-* ’^ = 150- = 150•8.1207 = 1218、П Л: Л Задача 1.53.Неровка намотана на неподвижный цилиндр, на одном конце которого подвешен груз Q. Сколько раз необходим

о намотать трос на цилиндр, чтобы он удерживал груз Q вертикальной силой P, приложенной к другому концу троса? Коэффициент трения троса о цилиндр равен/. Решение. Используйте формулу Эйлера. Таким образом, при ограничении равновесия, минимальное значение коэффициента р от силы П = КК 1А、 Где а-угол наклона троса цилиндра. Этот угол является Выпуск 1.53. Здесь n-полное число оборотов каната, которое п

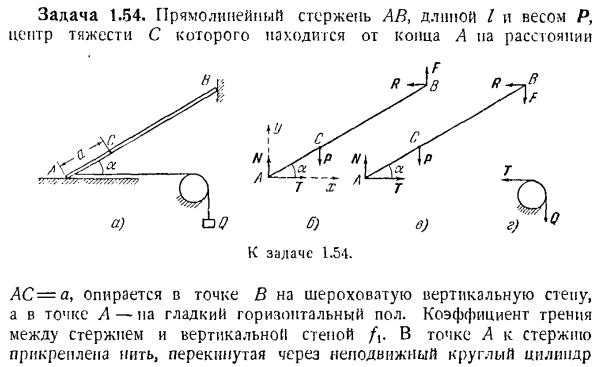
рибавляется к углу mc / 2 со стороны действия каждой силы. Подобный этому Логарифм, находим： В Q-в P = / *(2π+ 1), 1 / в Q-в P Откуда? н. −1. Задача 1.54.Линейный стержень AB длины I и веса P с центром тяжести на расстоянии A К выпуску 1.54. Он расположен на AC-a, пункте B в грубом вертикальном шаге, и пункте A в ровной горизонтали floor. At точка коэффициента трения а между штоком и вертикальной стенкой, резьба прикреплена к штоку и переброшена через неподвижный круглый цилиндр

вен/.Тогда сила T, необходимая для поддержания нагрузки P в равновесии, определяется по формуле Эйлера. Рис. 1.41. ш Р — А. (14 *） Т = Ре Где E-основание натурального логарифма. Таким образом, сила T для уравновешивания нагрузки P не зависит от R диаметра цилиндра и является функцией угла охвата и коэффициента трения. Для решения задачи о равновесии твердых тел при наличии трения гибких нитей、 Первые 4 пункта перечислены в начале книги. 15.Следующий： 5) сравните числоТу же проблему можно решить и другим способом. Рассмотрим общее равновесие кабеля(рисунок а), общий угол охвата каб

еля 2 валами 3.3 В: у меня *. 2 * = ’ Найдите отношение между силой P и силой Q. Вопрос = ПК ’ ТФИ У нас есть： Для определения величины нагрузки P, которую можно удерживать в равновесии при нагрузке Q = 10 кг, находим следующую формулу из(3): £ — =3и: / = 2.358. И затем… f = 10,5 и P = 10-10. 5 = 105 кг. Таким образом, нагрузка Q 10 кг может удерживать нагрузку P 105 кг в равновеси

и. Задача 1.51.Кабель AB охватывает барабан, вращающийся вокруг центра O. коэффициент трения кабеля о барабан равен/. Обруч кабеля Liv установлен на плохом рычаге и может быть вращан вокруг пункта D. расстояние AI)= a, BD-B. Си. Г в 6 I A X О е.） о.） СЗ. б.） ymq. К выпуску 1.51. Определите натяжение троса в точках А и В. Если вес неисправного рычага проигнорирован, то

груз Q подвешивается к рычагу так, что давление в точке D равно нулю, расстояние CD = C. Решение. Рассмотрим равновесное состояние троса, охватывающего барабан, и мысленно отбросим рычаг (рис. Согласно формуле (и*), соотношение между этими напряжениями определяется по формуле: £=(1） Потому что угол кабеля барабанчика tf. (1) индекс является положительным. Потому что, по отношению к предопределенному направлению вращения барабана, напряжение^ сидит Далее, в соответствии с условиями задачи, рассмотрим равновесие плохого рычага, предполагая, что давление в точке D, а следовательно и р

еакция шарнира D, равна нулю. Активная сила Q действует на рычаги. Мысленно отбросьте кабель и замените его действие реакцией 6 \и S&(рисунок C).Очевидно= ^ =, Выберите координатные оси для создания уравнения равновесия == (2) 2 мкр (ФК) = КК-З \ А ’^ Б =0.(3） 3 уравнения с 3 неизвестными S’V S ^ s（1）、（2）、（3）система была полуВы можете увидеть последнее case. In в этом случае примененная точка обхода N неизвестна. Составьте уравнение равновесия-сумма проекций всех сил на координатные оси (рисунок Б) равна нулю%Fkx=P Cos 30° — F,=0, 2Fky=N+P sin 30° — Q=0.In кроме того, это относится к силе м

ышечной силы против самого давления. Если сила силы определяется из этого уравнения и сила силы и a / отклоняются от уравнения, используется следующее уравнение. p. s.-19 _ — __— 4] 5 кило. ~ ~ cos30°+ / sin30°0.965~ ~ ^ ’K1′ Если это значение больше, чем это, блок будет скользить к колену. (зенитный.)Для этого она необходима. Определите вес нити в невесомости, состояние, в котором степень равновесия изменяется. Решение. Рассмотрим баланс стержней АБ, мысленно отбросив вертикальные стенки, горизонтальные ИОЛ и горизонтальные нити, заменив их действия на reaction. It есть случай sensitive. It делится на 2 случая. 。

Для степеней a. In в этом случае точка переместится к человеку заранее, точка down. As в результате сила F становится направленной вверх (рис. Таким образом, стержень АВ (рис. Б) под действием следующих сил будет находиться в равновесном состоянии йода: вертикальная реакция N, натяжение нити G, масса P, вертикальная реакция I и сила трения F Он образует квадратное уравнение пластиковой бутылки. о(2） ^Fky=N-P+F=0、 £ТП(ФК)= — N1cos а+/>(/- а)потому что+77sin а=0(3） Кроме того, в нем описывается сила прямого давления в точке В. Ф=ф, Р Учитывая, что сила трения, приложенная к цилиндру, направлена п

о часовой стрелке, зависимость натяжения нити от силы Q из 7 выглядит следующим образом (формула Эйлера). Мой метод сотрудничества и Формула следующие: Если вы введете значения больших (3) n и 7, вы в конечном итоге сделаете вид, что это: Другие особенности включают в себя: 。В случае с Da Sanya. In в этом случае точка а перемещается до месяца, Точка Б -.И наоборот, встречный ветер направлен вниз(рисунок), а сила, действующая на рулевое управление цилиндра, направлена против часовой стрелки. Фото уравнение уравнения AB eltium выгляди

т следующим образом. 7 — / ㎡ = да、 Н-П-Ф=О、 — L7cos a-j-P (/- a) cos a+77sin a=0. Кроме того, она определяется равенством. Ф↓ / ,/= 。Мне это нравится. R n f kokuku из SL Lee click et al, следующий не говорят. ’=’- F x c c — >>1.In кроме того, если вы введете значение N T в выражении moment, произойдет следующее: тг. Максимальное значение имени a в Формуле Лиона по сравнению с оценкой Лиона. б.） С 0171 по 33. Я собираюсь рас

следовать это дело на второй день. Если блок, вероятно, будет аппроксимирован вокруг Брива A, нормальные противоположные силы N и сила F применяются к точке A. Большая змея 3 к заготовке, а также 4-й глаз к заготовке-мышечная сила сопротивления постоянному току для создания хорошего в ПХ-п cos30° — ф=0,(1） Fky v=N-Q H-P sm30°=0,•(2） V uA(Fh) — Q’y-P сж1g=O, (3） Ф=ФН. (4)）

Смотрите также:

Предмет теоретическая механика

Произвольная плоская система сил. Случай параллельных сил	Графическая статистика и методы расчета ферм
Равновесие системы твердых тел	Система сходящихся сил