Оглавление:

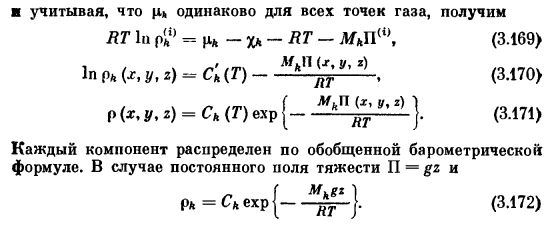

Равновесие смеси идеальных газов в поле внешних сил
- Рассмотрим задачу о равновесии идеальной смеси газов в силовом поле, таком как гравитационное поле. Весь объем делится газом, затем на отдельные фазы и бесконечно малые однородные parts. In этот случай, i фаза =Ф1**(4-й.4’,.• * ) +П° ’ SMknK, (3.163) где F «’-свободная энергия без гравитационного поля, п ⁽ о-потенциал гравитационного поля I-й единицы массы.
Фактически к этому результату пришёл уже Сади Карно в сочинении «О движущей силе огня и о машинах, способных развивать эту силу». Людмила Фирмаль
Фазы л / — молярная масса компонента с номером K, и N * ’ — молярная масса k-го компонента ЛТХ фазы. Условия равновесия (§ 45) химический потенциал каждого компонента (3.164) 。То же самое для всех точек в объеме.
- Это то же самое в занятом миксе. В этом случае для 7⁷ 1⁰ необходимо использовать представление свободной энергии смешанного газа. Полученное в§ 46 (обозначено F). Здесь P ⁽’- объем 1-й фазы. Дифференциация, мы имеем _l, за₊ложь ^ + ЛГ、 (3.166) (3.167).
Введение объемной концентрации k-го компонента в i-м молярном числе на единицу объема: (3.168) ■Задано| x>одинаково для всех точек РТ Лу Пи, » = г * — х * — РТ- 。 , М, р(х, y、 р *(О, З)=Cₖ (Т) — — — — — — — jjy ——、 П («.U. r} = CK (G) exp■- Газ, мы получаем (3.169> (3.170) (3.171).
Второе начало термодинамики задаёт ограничения на направление процессов, которые могут происходить в термодинамических системах, и исключает возможность создания вечного двигателя второго рода. Людмила Фирмаль
Каждый компонент распределяется по выражению. Для констант СР-Дж.- Обобщенное барометрическое гравитационное поле P-gz и (3.172).
Смотрите также:

