Оглавление:
Равновесие системы сочлененных тел
Системой сочлененных твердых тел называется конструкция, состоящая из нескольких твердых тел, свободно опирающихся друг на друга и соединенных между собой какими-либо нежесткими связями (шарнирами, гибкой нитью).
В соответствии с принципом отвердевания, совокупность сил, действующих на любую систему тел, должна при равновесии этой системы удовлетворять соответствующим условиям равновесия абсолютно твердого тела. Эти условия, являясь необходимыми условиями равновесия, в случае системы нежестко скрепленных тел будут недостаточными и из них нельзя определить все неизвестные величины.
Так, например, применяя принцип отвердевания и рассматривая равновесие трехопорной горизонтальной балки с промежуточным шарниром, находящейся под действием плоской системы вертикальных сил (см. задачу 15), можно составить только два независимых уравнения равновесия, неизвестных же реакций опор будет три.
Так как при равновесии системы тел каждое тело системы находится в равновесии, то задачи на равновесие системы сочлененных тел обычно решаются путем рассмотрения равновесия каждого тела в отдельности.
При составлении уравнений равновесия какого-либо тела системы мы должны рассматривать другие, сочлененные с ним тела как связи и заменять их действие на рассматриваемое тело реакциями этих связей. При этом всегда нужно иметь в виду, что силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Иногда бывает выгодней рассматривать сначала равновесие всей системы сочлененных тел в целом, а затем уже равновесие отдельного тела. Составляя уравнение равновесия всей системы тел в целом, мы рассматриваем ее как абсолютно твердое тело, и потому в эти уравнения не войдут силы, с которыми действуют друг на друга отдельные тела системы. Последнее следует и из того, что силы взаимодействия между каждыми двумя телами системы равны по модулю и прямо противоположны по направлению, и потому сумма проекций этих сил на любую ось так же, как и сумма моментов их относительно любой точки, равна нулю.
Пример задачи:
Найти реакции опор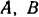 
и 
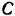трехопорной горизонтальной балки с промежуточным шарниром (рис. 64, а). Расположение опор и вертикальных нагрузок на балку указано на чертеже, причем по модулю последние равны между собой: 
.
Решение:
Балку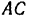 
можно считать составленной из двух балок: консольной балки 
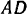и подвесной балки 
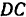. Действие одной балки на другую, передаваемое через связывающий их шарнир 
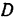, можно заменить реакциями шарнира 
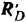и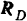 
. По закону равенства действия и противодействия сила 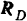с которой консольная балка действует на подвесную, равна по модулю и противоположна по направлению силе , с которой подвесная балка действует на
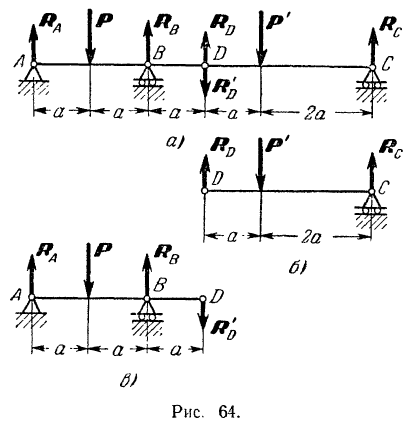
консольную. Эти реакции, так же как и реакции всех опор, при данном расположении опор и направлении активных сил 
и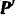 
могут быть только вертикальными.
Из условий равновесия балки 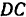(рис. 64,6) находим
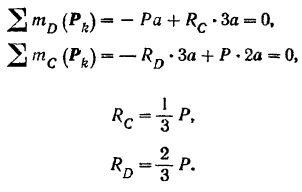
Давление подвесной балки на консольную равно
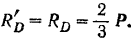
Из условий равновесия консольной балки 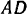(рис. 64, в) можно найти реакции двух других опор:
Пример задачи:
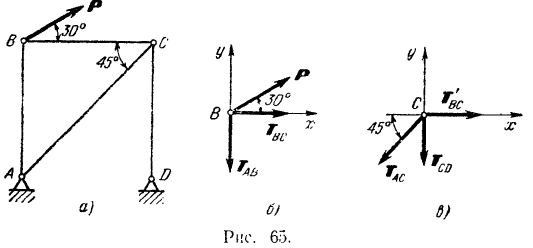
В стержневой системе, изображенной на рис. 65,а, стержн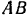и 
и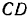 
вертикальны, стержень 
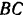горизонтален. Шарниры 
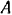и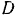 
неподвижны. На узел 
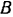действует сила 
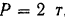, направленная под углом 30° к стержню 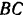. Пренебрегая весом стержней и считая все шарниры идеальными, определить усилия во всех стержнях.
Решение:
Рассматриваем сначала равновесие шарнира 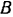, к которому приложена единственно известная нам сила 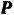. Освобождая шарнир от свечей, заменим действие на него стержне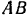й и 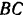реакциями этих стержней на ось шарнира. Так как все шарниры — идеальные и весом их можно пренебречь, но реакции стержней будут направлены (стр. 35) вдоль стержней. Сторона же их направления нам неизвестна. Будем пока считать, что стержни растягиваются и потому их реакци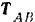и 
и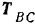 
на узел 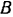направлены так. как показано на рис. 65, б.
Проводим оси координат так, кап показано на том же рисунке, и составляем уравнения равновесия сил, приложенных к узлу :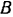
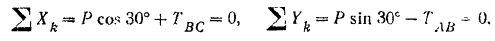
Решая эту систему, находим:
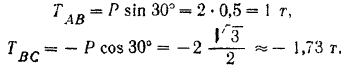
Отрицательное значение, полученное для реакции стержня 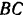, показывает, что принятое ее направление надо изменить на противоположное и, следовательно, этот стержень не растянут, а сжат.
Переходим теперь к узлу 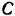. Он находится в равновесии под действием трех сил: реакции 
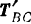стержня 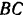на узел 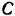и реакци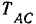й 
и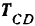 
стержне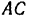й и 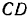на тот же узел. Так как реакции стержня на противоположные узлы, которые он соединяет, всегда равны по модулю и противоположны по направлению, то реакция 
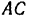и, следовательно, нам известна. Предполагая пока, что стержни и 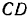растянуты, направляем их реакци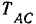и и 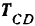так, как показано на рис. 65, е. Проведя оси координат так, как показано на этом рисунке, составляем уравнения равновесия сил, приложенных к узлу :
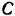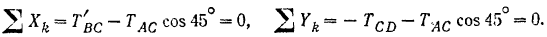
Решая эту систему, находим:
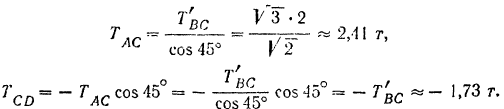
Отрицательное значение, полученное для реакции 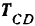, показывает. что ее направление надо изменить на противоположное и что стержень 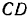сжат, а не растянут.
Пример задачи:
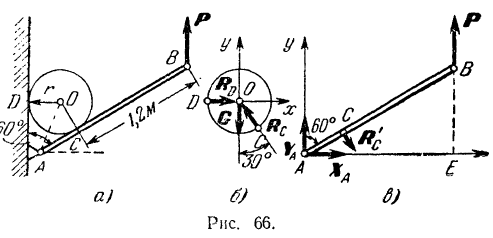
Однородный шар весом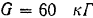 
, радиуса 
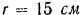опирается на гладкую вертикальную стену и гладкий стержень 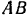, шарнирно связанный со стеной в точке 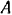(рис. 66,а). Пренебрегая весом стержня 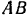, определить вертикальную силу которую надо приложить в точке 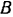к стержню для того, чтобы система была в равновесии, реакцию шарнира 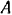и давление шара на стену. Расстояние от точки 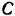касания шара со стержнем до точки В приложения силы 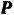равно 1,2 м. Угол 
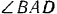равен 60°.
Решение:
В данной задаче мы имеем дело с равновесием системы, состоящей из двух тел: шара и стержня.
Рассмотрим сначала равновесие шара, заменяя наложенные на него связи их реакциями. Шар находится в равновесии под действием следующих сил: силы 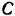тяжести шара, приложенной в его геометрическом центре, реакции 
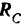стержня и реакции 
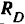стены (рис. 66,6), проходящих соответственно через точк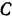и 
и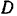 
касания шара и нормальных к его поверхности. Таким образом, приложенные к шару силы сходятся в центре шара.
Выбрав направления координатных осе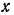й 
и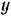 
(рис. 66.6), составляем два уравнения равновесия для данной плоской системы сходящихся сил.
Реакция 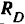гладкой вертикальной стены перпендикулярна к ней. Стержень 
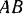составляет с горизонтом угол в 30°, и, следовательно, угол между нормальной реакцией 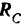этого стержня и горизонтальной осью 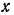равен 60. Имеем:
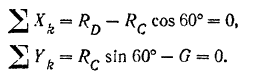
Решая эту систему, находим:
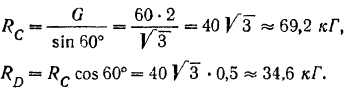
Для определения приложенной к стержню 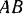силы 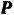и реакции шарнира 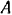рассмотрим равновесие стержня 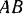. К нему (рис. 66, в) приложены вертикальная сила 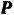, давление 
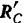шара на стержень, равное по модулю и противоположное по направлению найденной выше реакции 
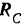стержня на шар, и неизвестная реакция шарнира 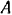. Разложим последнюю на две составляющие: горизонтальную 
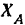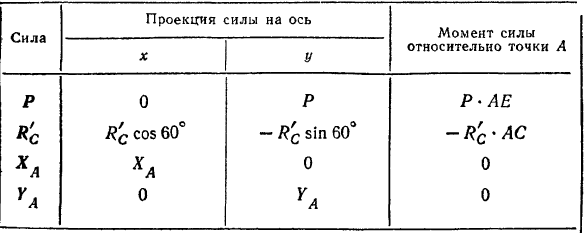
и вертикальную 
. Выбрав оси координат и приняв за центр моментов точку , находим проекции данной плоской системы сил на координатные оси и алгебраические величины моментов всех сил относительно точки .
Из треугольника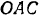 
(рис. 66, а) находим:
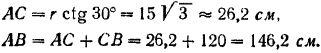
Из чертежа (рис. 66, в) находим плечо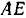 
:
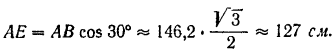
Составим уравнения равновесия:
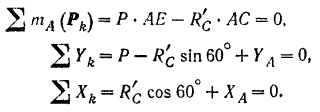
Решая эту систему, находим
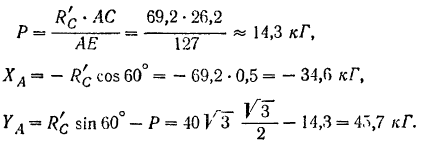
Знак минус перед значением реакции 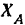указывает, что она в действительности направлена в сторону, противоположную предположенной, т. е. направлена влево.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
