Равновесие системы твердых тел

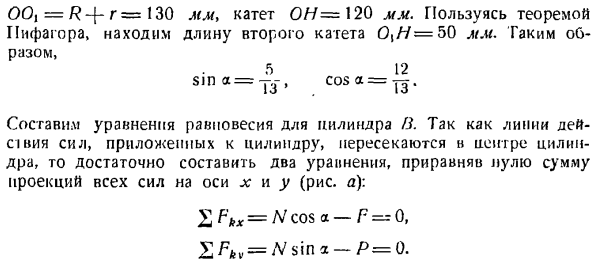
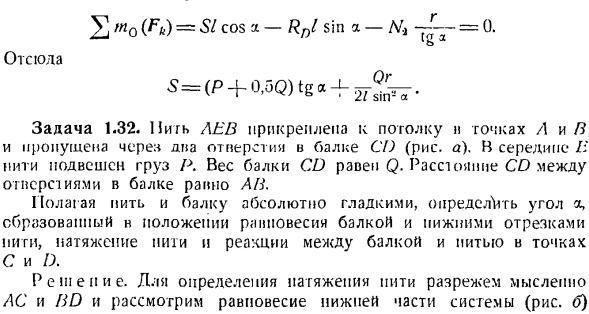
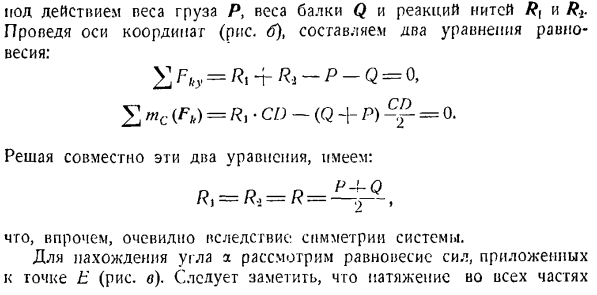
Равновесие системы твердых тел

• Равновесная система твердых тел В статике твердого тела, помимо равновесия 1 объекта, рассматривается совместная система материального объекта, то есть совокупность твердых объектов, соприкасающихся друг с другом на поверхности или соединенных между собой шарнирами, гибкими нитями или стержнями. Важной задачей статики в твердых системах является определение реакции связывания.

Главным для этого является метод ампутации, при котором, помимо равновесия всей системы организма, учитывается равновесие отдельных органов (или групп органов систем account. In кроме того, все остальные органы системы, а воздействие на организм, где рассматривается равновесие, заменяется реакцией.

И соответствующие связи разрушаются мысленно Людмила Фирмаль

Если рассматривать равновесие всей системы твердых тел, то реакция связей между телами, входящими в систему, является、 Подставляя значение Р = 30 кг, находим следующее: L / = 78 кг, F = 72 кг. Цилиндр A находится в равновесии под действием 4 сил: веса Q, горизонтальной силы реакции стенки S, вертикальной силы реакции пола T, величина силы реакции N ’ цилиндра B равна и противоположна силе N. 4, мощность (рисунок D) все пересекаются в точке O, центре цилиндра a.

эти силы составляют 2 уравнения равновесия. сумма проекций сил на ось l: а ось y равна нулю： £Fkx = С-Н соѕ а = 0、 2 fky по:= Т-Q-А / С и н = 0. Я найду тебя отсюда.： 5 = 72 кг, Т = 70 кг. Следует отметить, что эту задачу можно решить и другим графическим способом. Действительно, зная величину и направление силы Ru, а также направление сил N и F, мы создаем треугольник замкнутых сил.

• Этот треугольник совпадает с треугольником 00 {H (рисунок C).Если стороны O, H установлены равными силе P, то сторона OH дает силу F в том же масштабе, а сторона OOx дает N. Далее построим замкнутый силовой многоугольник силы, которая будет приложена к цилиндру А. построение начинается с Силы, величина и направление которой известны N и Q. 

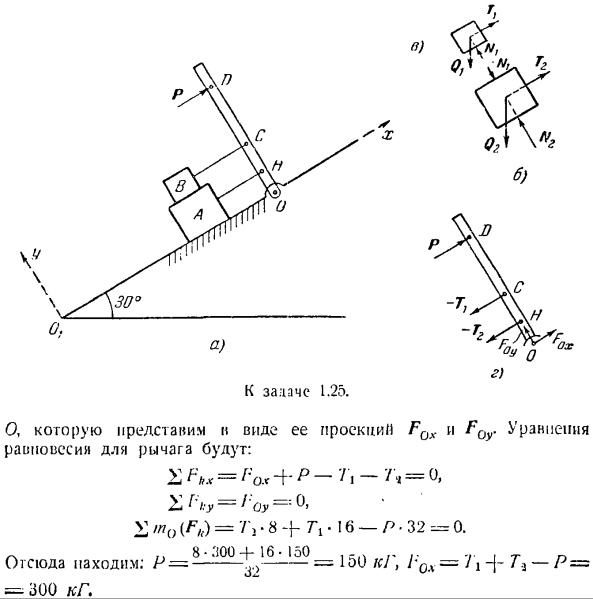
Задача 1.25.Блоки Liv весом 600 и 300 кг, соответственно, уравновешиваются на гладкой плоскости, наклоненной йодом под углом 30°по отношению к горизонтальной линии силой Р, параллельной ОО, с помощью рычага ОД, перпендикулярного наклонной плоскости (рис. а).Кабель, соединяющий рычаг с блоком, также параллелен плоскости ООТ.

Силовые полигоны, ребра на выбранном масштабе определяют неизвестные силы. Людмила Фирмаль

Она определяется путем игнорирования трения, силы троса и величины силы R. расстояние OI-N СМ, NS-N СМ, CD = 16 см. Решение. Рассмотрим баланс каждого блока и баланс рычагов отдельно. Блок а (рисунок Б) находится в равновесии под действием 4 сил: натяжения Qit массы, параллельной наклонной плоскости реакции NB, перпендикулярной реакции N и 00 / грани Блока В.

Выберите координатную ось xy (рисунок A) и создайте уравнения равновесия. 1x = 7 * — Qi sin 30°= 0, \ vFky = K. l-Qi cos 30° — = 0. Дж 7-2 = вопрос греха 30°= ’g 300л. Блок в (рисунок С)находится в равновесии под действием 3 сил: реакции перпендикулярной плоскости 00 Нлт массы Q, и натяжения параллельной плоскости 00 ипок 7.

Создайте уравнение равновесия. 7-I-Q, sin 30°== 0, ZPky = M-Qi cos 30°= 0 Я найду тебя отсюда.： Tt = Ql sin 30°= 150 кг, N, = 150/3 кг. Из 2-го уравнения системы (1) получаем следующее: ЛД = м, Косинус 30° — ф ЛГ= 300•КЗ + 150/3 = 450 [/ с ’Г. Зная натяжение троса, рассмотрим баланс рычага под действием силы (рисунок D): I, — Tlt-и шарнирное противодействие По зат Эвия 1.25. 0, что выражается в проекции форматов F0x и F0y.

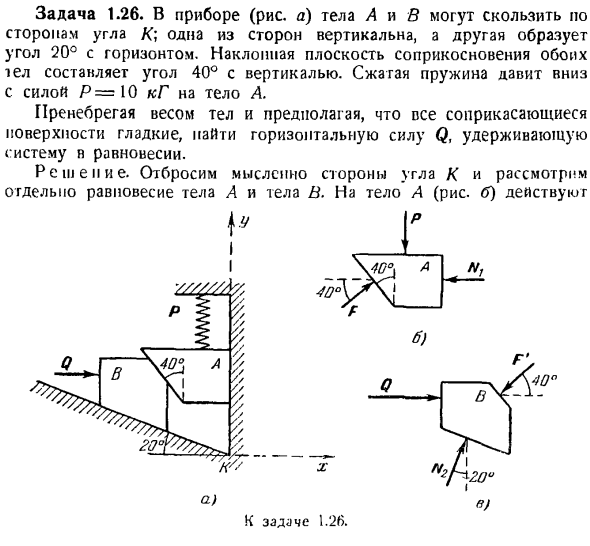
Уравнения для рычагов pa и веса и I следующие: PPbx =Γ: o.<+ P — — — ’ / * = 0、 £[’ку = 1′ ой =： Y, m0 (F / t)= 7 * 3•8 + 7е!- 16 — />-32 = 0 РВ /> 8-300 + 16.150,, .. …、- Найди его отсюда. P = — — — — — = 1o0 k1, r0x = J 1 — \ — T ^ — P = = 300 кг. Задача 1.26.In устройство (фиг. а), корпуса А и В могут скользить вдоль боковой части под углом/ С. 1 на боковой стороне является вертикальной, другая 1 образует горизонтальную линию и угол 20°.

Наклонная плоскость обоих контактов 1el образует угол 40°по отношению к вертикали. Горящая пружина прижимается к корпусу а с усилием Р = 10 кг. Игнорируя вес объекта, находим горизонтальную силу Q, которая удерживает систему в равновесии, предполагая, что поверхность контакта Ди гладкая. Снова войдите, т. е. мысленно отбросьте обе стороны угла K и рассмотрите равновесие между телом A и телом B отдельно. Тело (рис. Б) строительство П. С.

К задаче 1.26. 3 силы: вертикальное нисходящее давление P весны, вертикальная реакция стены / vis. Направленная горизонтально влево, реакция F отброшенного объекта B перпендикулярна наклонной контактной поверхности обоих объектов.

Рабочие линии этих сил пересекаются в 1 точке. Это связано с тем, что объект а находится в состоянии равновесия под действием 3-х непараллельных сил, находящихся в одном и том же plane. So, для них достаточно создать 2 уравнения равновесия, в которых сумма проекций всех сил на оси l *и y равна нулю. Выберите ось, как показано на рисунке. а потом….. £Fkje ^ Fcos 40° — D7 / = 0、 2 Fkx = F sin 40-й

Пони, неизвестны горизонтальная сила Q и реактивная сила 7V. j. поскольку угол перпендикулярен наклонной стороне, он образует угол 20 градусов относительно вертикали. Мы опишем эти 3 Силы, где в 1 точке пересекаются 2 уравнения равновесия. £ / ^ = <2 + Af » sin 20° — F cos 40°= 0,£Fky =Л / acos 20° — F sin 40°= 0. Подставляя значения Ft, описанные выше в этих уравнениях, мы определяем оставшиеся силы Q = 8.3 к G, Nt = 10.6 к G.

Задача 1.27.2-пролетная балка AD (рис. а) с промежуточным шарниром C поворачивается в точке A. At пункты B и D, Луч поддержаны горизонтальным роликом используя ролик. И\ (1 Q Q * SP g-g ч а » * <РЖ р и Р rcx следует 4> К задаче 1.27. г \ п 1/7 Иу1 Я Я… Х. с.） Если… ПГ. Определить силу взаимодействия шарнира C с реактивной силой опоры A, B, D, если на балку действует следующее: пара сил в момент M = 20 к1м}сила I = 8 кг, сила Q = 12 г. размеры даны: AE = 4 Вт, EB = 2 м, BC = 3 Вт, CH = HD = 2 

Решение. Система твердых тел состоит из 2 балок. Рассмотрим равновесие каждого луча отдельно. ПА динамике работает (рисунок Б): активная сила Р и пара активных сил в момент м. Далее к балке добавляется соединение-шарниры а и с, подвижная опора В. мысленно отбрасываем соединения и заменяем их поведение реакцией. Поскольку реакция шарнира а неизвестна по направлению и величине, его заменяют на 2 компонента RAX и RAv.

Аналогично, сила реакции сустава C представлена 2 компонентами RCx и RCy, а сила реакции опоры B выражается вертикальной силой RH. In кроме того, равновесие пучка AS считается равновесием свободных твердых тел под действием 6 сил и 1 силы. Выберите координатные оси из точки A в качестве начала координат и укажите горизонтально справа от горизонтальной оси и вертикально вверх.

Создайте уравнение равновесия для пучка переменного тока. C) (2) (3） Они-Ракс- ту = Ра+ » в + КС-Р = ^. ма(ФК)= РБ. АВ- \ замените ■ АС-П ■ АЭ-М = 0 Вместо 2-го уравнения равновесия можно создать сумму моментов всех сил, связанных с точкой С. это уравнение содержит 2 неизвестные силы J? АВ и линия действия Другие неизвестные силы пересекаются в точке С. Однако в обоих случаях уравнение(1) не зависит от остальных уравнений и содержит 2 неизвестных.

Уравнения(2)и(3) взаимосвязаны и содержат 3 неизвестных. Следовательно, 1 неизвестный не может быть определен из полученного пирога system. So, рассмотрим равновесие 2-го пучка CD (рисунок C). 1. применяем закон, что одна активная сила Q действует на балку и освобождает ее от муфты, заменяя действие шарнира C реакцией муфты. Реакция Rn направлена перпендикулярно горизонтальной плоскости, на которой расположен ролик.

Шарнир с реакция неизвестна по величине и направлению. Исходя из закона действия и равенства реакций, компоненты этой реакции по модулю равны компонентам реакции шарпия, приложенным к пучку лекарственного средства, и направлены в прямо противоположном направлении(рис. Таким образом, возникает свободный твердотельный пучок, находящийся в равновесии под действием 5 сил. («Оставьте уравнение равновесия и выберите координатную ось с точкой C в качестве начала координат.

Горизонтальная ось направлена вправо вдоль балки, а вертикальная ось направлена вертикально вверх. 2Fkx = — RCx = 0, (4） 1 ф ’ \ г = — Щ-замените = о,(5） в; МС(ФК) — РД * компакт-м * Си =0.(6） Эти 3 уравнения равновесия имеют только 1 новый неизвестный RIr, и все 6 уравнений равновесия имеют 6 неизвестных. Из Формулы(4)и (I): Rqx = RAX = Из уравнения (6)можно увидеть: = 12.2 / 4 = 6 * G、 (5) что получается из： Р0 = РД-Д = 6-12 =-6 л-г.

Знак минус фактически указывает на то, что направления компонентов RCv и R’CV противоположны тем, которые приняты на диаграмме. Далее, из (3)： R » = PM + AD-K: M1 = 8-4 / ’6-G 20/6 −1-6-9 / 6 = 17.66 G, наконец, из(2)、 RAy = P-Rb-RCv = 8-17. 66-f 6 =-3.66 i’G. Это надо учитывать. Они не входят в уравнения равновесия как взаимно уравновешенные силы внутри.

А если учесть равновесие групп тел, входящих в отдельное тело или систему, то реакция соответствующих связей, разделенных мысленно, становится внешней силой и входит в уравнение равновесия равновесия. Задача равновесия твердой системы под действием плоской системы любой силы решается путем применения уравнения равновесия твердого тела, которое описывается в§ 2 (уравнение (1) или (2), или (3)).

В качестве примера рассмотрим твердотельную систему, которая показана на рисунке. 1.33, 1.34. Шатунно-кривошипный механизм OAB (рис. 1.33) состоит из 3-х тел: кривошипа OA, шатуна AB и ползуна B. Эти тела соединены между собой шарнирами A и B. O и горизонтальной направляющей для предотвращения вертикального перемещения ползуна B. 

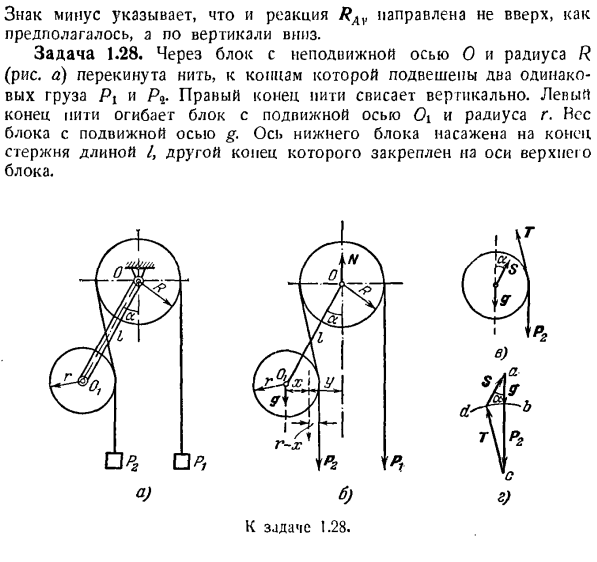
Рис. 1.33. Знак минус указывает на то, что реакция RAv направлена вниз, а не вверх, как ожидалось. Задача 1.28.Нить забрасывается в блок с фиксированной осью O и радиусом R (рис. а), и подвешиваются 2 одинаковых груза

Определите угол i, игнорируя подшипник стержня. Угол i, образуя стержень вертикально в положении равновесия, прикладывают к стержню усилие{ = 10 кг, g = 4 кг, R = = 4 см, R = 3 ci/, / = 10 rj /. Решение. Рассмотрим равновесие твердой системы, состоящей из 2 блоков и стержня, соединяющего их центры(рис. Б).

для этого мысленно отбросьте ось о, поддерживающую верхний блок, и замените ее отдачей N. In кроме того, на систему действует внешняя сила Pb P. g> g. Все остальные силы, очевидно, перпендикулярны, поэтому реакция N перпендикулярна.

Для этой системы параллельных сил мы создаем 2 уравнения равновесия.%Fiy = N-P {- P ^ — g = 0、 £flf0(^ я)= м /? — фут(/ грех-Р) — гл грех = 0 Из первой Формулы определите реакцию 7В. Н = м + Р3 + ^ = 24 Из 2-го уравнения найдите угол a. С-4-10(10 грехов-3) — 4-10 грех-0、 Оттуда грех А = 1/2, а = 30°. Чтобы определить силу стержня, рассмотрим равновесие блока и движущегося axis.

It находится в равновесии под действием 4 сил(рисунок с): веса g, реакции 2 нитей и размера T, а также реакции стержня вдоль, но величина неизвестна. Поэтому геометрическая сумма этих 4 сил должна быть равна нулю. Поскольку угол a известен и равен T = Pb, проще всего определить значение 6 *графически, создав силовой полигон.

Отложим от точки a (рисунок D) 2 вертикальные силы, g, и по шкале, выбранной для force. In кроме того, нарисуйте дугу окружности равного по размеру радиуса от точки С, которая является концом силы I, как от центра. На этой дуге будут находиться конец силы T и начало силы S, а по вертикали и угол a = 30°.

под углом 30 градусов от точки a проведите прямую линию, перпендикулярную точке пересечения с дугой точки d, соедините точки d и c прямой линии. Определите величину усилия стержня с разрезом da. By измеряя по шкале, выбранной для силы, мы видим, что сила стержня равна S = o кг.

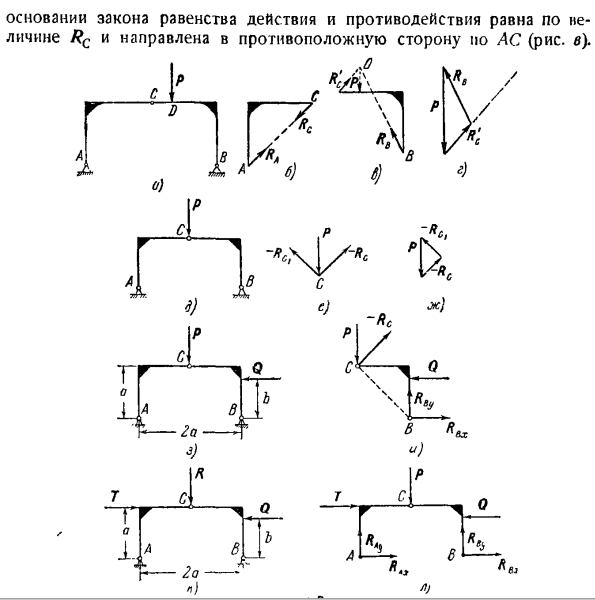
Задача 1.29.Каркас состоит из 2-х жестких частей AC и BC (рис. а), соединенных шарниром C и прикрепленных к фундаменту шарнирными опорами A и B. Если вертикальная сила P = 1 t приложена в точке D, то шарниры a, B> c \определяют реакцию. Задача решается графически. Решение.

Реакция шарниров A и B неизвестна по размеру и direction. So, рассматривая равновесие всей системы АСВ, отбрасывая опоры А и в, заменяя их действия реакциями, неизвестных будет 4, а уравнений равновесия будет 3. Таким образом, мы учитываем равновесие на левой стороне рамы отдельно(рисунок B).к этому твердому телу не прилагается активная сила.

Примените bond waivers™, мысленно отбросьте петли A и C и замените эти действия реакциями. Часть рамы динамика находится в равновесии под действием 2 сил: RA и Rc. Согласно 2-му закону статики, эти силы равны по величине и должны быть направлены в разные стороны вдоль 1 Прямой.

Поскольку к точке А приложена сила 1, а к точке с-другая сила 1, AC становится общей линией действия для этих сил. Кроме того, рассмотрим равновесие правой стороны Солнечного каркаса. Р. 1 к нему прикладывают активную силу, освобождая мысленно от 2 связей (шарниров В и с), заменяя их действие реакцией.

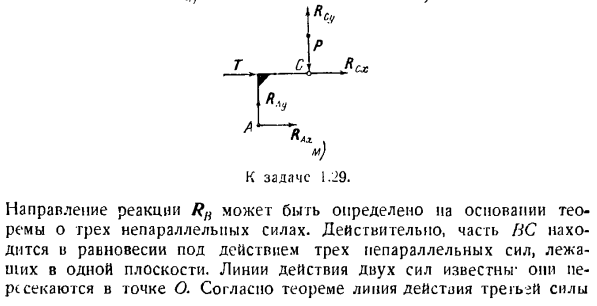
R’c реакция на Основа закона равенства действий и реакций равна по величине К/ С и направлена в обратном направлении вдоль АС(рисунок с). К-ТГ-Ч Г-7 \ Л ’ 4-л Л А Б) б） Да.） — Р.、 И с.） В Р *） Q. Мистер а — $ Я/? икс П. С. Но… У’ 6. 2а о） Л.） К выпуску 1.29. Направление реакции Rfi может быть определено на основе теоремы о непараллельности синуса forces.

In дело в том, что часть летательного аппарата находится в состоянии равновесия под действием 1 непараллельной силы, которая спокойно лежит в одной плоскости. Линии действия 2-х сил известны, и они пересекаются в точке О. линия действия 3-й силы, согласно теореме Реакция Rn должна также проходить через точку O. 3 силы P, R’c, Rfi, рабочая линия которых пересекается в точке O, находятся в равновесии.

Поэтому они должны образовывать замкнутый треугольник. Отойдите от любой точки (рисунок D) и установите силу P, чтобы узнать величину и направление. От конца силы Р проведите линию, параллельную АС, то есть линии действия силы R’c. от начала силы Р проведите линию, параллельную Об, то есть линии действия силы Rn.

Получаем треугольник замкнутых сил. Его стороны определяют масштаб желаемой реакции, которая принимается силой П. Из сил, действующих на 3-х шарнирную арку, если существует 1 сила, действующая на шарнир C, решение задачи определения реакции 3-х шарнирной арки шарнира является complicated.

In в этом случае рассмотрим 3-х шарнирную арку как связное 3-х корпусное устройство: 2 половинных арки и болт с шарнирами. Полудуги не касаются друг друга. Шарнирные болты находятся в контакте с каждым из них. Рассмотрим 3 возможных варианта решения проблемы.

В первом варианте(рис. е) активная сила Р приложена к шарнирному Болту, а заданная сила не приложена к полуарке. в случае eyum на левое равновесие, находящееся в равновесии, воздействуют 2 равные силы RA и Rc (рисунок B), направленные прямо в противоположную сторону от AC. Так же, как и в правой полудуге, существуют 2 взаимно уравновешивающие силы ПК, направленные на прямую линию.

Рассмотрим равновесие шарнирного Болта S. 3 применяются силы: сила P, правая и левая полудуговая реакция-Rc, — RCl (рисунок C), а сила P известна по величине и направлению, известна только линия действия для полудуговой реакции. Если мы создадим замкнутый треугольник (рисунок G), то найдем значения реакций Rc, RCi, в результате которых значения RA, Rn будут равны.

Во 2-м барьере золы (рисунок L), активная сила, кроме шарнирного Болта! C применяется только к 1 правой половине дуги (сила Q).Рассмотрим равновесие левой половины арки (около фигуры).Направление реакции Rc и Ra совпадает с прямым AC.

Далее шарнирный Болт C крепится к правой половине арки с действующей силой P, и под действием этой силы учитываются равновесие (рис. I) и йод: P, Q — реакция Rlit, разложенная на Rc и 2 компонента Rlix, R.] y. — Обратите внимание, что Rc образует горизонтальную линию и угол 45°, создайте 3 уравнения равновесия. = Rc cos 45° — Q-I-Rnx = 0, Fky = Rc sin 49° — P + Rny = 0、 S » in(Fk)= Rc * V < ’ — P-cL-Q’b =0.

Все 3 неизвестных устанавливаются. В 3-м варианте(рис. K) активная сила, за исключением шарнирного Болта, приложена к обеим половинным аркам. В этом случае сначала определяют реакцию шарниров а и B. To сделайте это, рассмотрите равновесие всей арки, мысленно отбросьте шарниры A и B и замените действие реакцией(рисунок L). 3 уравнения равновесия являются: 2IFky = RAy + RBy—P = 0,% niA(Fk)= Q. b r. a. P. D. a-\ — RBy.2а = 0.

Эти 3 выражения имеют 4 неизвестных: RXT RAyi Rnx, RBy. Чтобы создать 4-е отсутствующее уравнение равновесия, приложите усилие Р для крепления шарнирного болта и рассмотрите равновесие полудуги(например, левой дуги) (рис. м). в этом случае мы создадим уравнение равновесия. Это не включает в себя реакцию правой половины дуги на болт.

Такое уравнение равновесия состоит в том, что сумма моментов всех сил вокруг шарнирного болта с равна нулю. 5>СЛ)= ЛХ-а- » Лу-а = 0. Система этих 4 уравнений, RAx, RAy) Rl {xf Rliv является determined. In кроме того, если вы составите оставшиеся уравнения равновесия для левой половины дуги, вы найдете компоненты реакции правой половины дуги на RCx> RCy-Болт.

Чтобы определить реакцию левой половины арки на болт(в данном случае она отличается от реакции на болт правой половины арки), необходимо отдельно учитывать равновесие правой половины арки. Задача 1.30.Цилиндрическая чашка с радиусом R установлена на открытой стороне ровного горизонтального пола. Внутри стекла находятся 2 одинаковых шара радиуса r и веса P соответственно. Определите вес Q цилиндрической чашки, в которой шарик не опрокидывается. Стенки стакана идеально гладкие.

The solution. In чтобы определить желаемый вес стекла, мы отдельно рассмотрим равновесия 2 шаров (рисунок B) и равновесия стекла (рисунок C). (1a система из 2 шаров действует силой: вес каждого шара P прикладывается к центру шара, а противодействие гладкого пола T вертикально вверх; стеклянная стена Nj и Nb прикладываются горизонтально, а точки D и C прикладываются. Нарисуйте оси. ось X является горизонтальной, а ось Y-вертикальная.

Уравнение равновесия системы, состоящей из 2 шаров、 Поставьте цилиндрическое стекло (рис.1.34) вверх дном на горизонтальный пол и поместите в него 2 шарика. Система состоит из 3 твердых тел которые в контакте друг с другом: O цвета шрама, 0.2 шарика и стекла.1. внешняя система этого корпуса имеет одно внешнее соединение-гладкий горизонтальный пол.

При решении задач с равновесием системы организма, как правило, недостаточно рассматривать равновесие всей этой системы. Для всей системы равновесное состояние сводится к 3 уравнениям равновесия в плоской системе сил и к 2 уравнениям в плоской системе параллельных forces. In в этом случае число неизвестных может быть больше, чем число перечисленных уравнений.

Однако в этой ситуации система не может быть определена статически. Потому что если разделить систему на отдельные твердые тела и составить уравнения равновесия для каждого из них, то число новых неизвестных может быть меньше числа новых уравнений равновесия. Если таким образом число всех независимых уравнений равновесия, составленных для всей системы и ее отдельных частей, равно числу всех неизвестных, то такая задача определяется статически.

ВГД. 2 = T — <2P = 0, (2） £m0 (Fk)= Ni’Ab-POB =0.(3） 3-е уравнение-уравнение моментов-составляется относительно точки Oy, где пересекаются линии действия 3 сил, в том числе 2 неизвестных. Из первого уравнения это выглядит так: Н = Н%= Н-(4）

Из 3-го выражения вы можете увидеть следующее: (5） / в Донецк’ Кроме того, рассмотрим равновесие цилиндрического стекла(рисунок с).Сила, действующая на стекло: масса Q

Н [И Н являются точками D и C в случае реакций точками I и K, чтобы применить (П [= П \И Л^ =Л/ *это очевидно)рассмотрение стекло инкапсуляция момент, момент Н давление на пол и, как следствие, этаж реакция исчезнет, стекло точки K только в горизонтальной плоскости будет находиться.

Создайте уравнение момента, чтобы передать точку K 2 МК (ФК)= НЖ * СК-а / Дж * ЦТ-М Р =0.(си） Кроме того, принимая во внимание(6) — (4), можно: генеральный директор. АБ-В. / ? = 0, Присвоить этому уравнению значение L/, определенное в формуле (5): Л-М УР-Р 0В ’АН-г’ 01 {М ~ Н~ Р〜Р-АВ ~~ я » Однако ОБ ’ = 2р-2R, поэтому для баланса нам нужно неравенство.

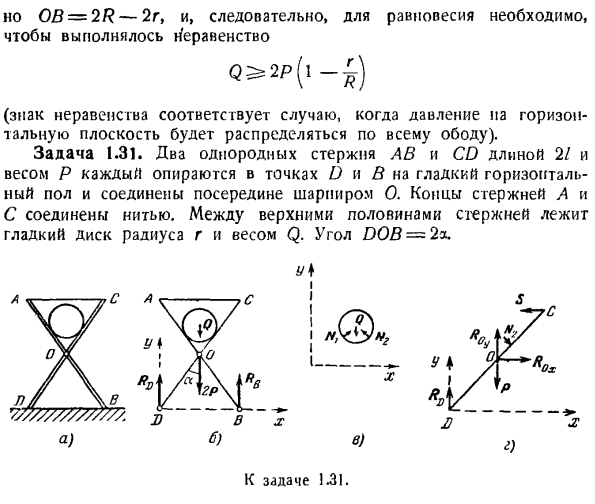
(Инфинитив соответствует случаю, когда давление на горизонтальную плоскость распределяется по ободу). Задание 1.31.2 однородные стержни длиной 2 /и массой P AB и CD расположены в точках D и B гладкого горизонтального пола соответственно, соединенных шарниром O посередине.

Стержни A и C соединены винтами. Между верхней половиной стержня расположен гладкий диск радиуса r и массой Q. угол DOB=.2а Один д） Задача 1.。31. Определите натяжение нити. The solution. In для того чтобы найти противодействие пола в точках D и B, рассмотрим равновесие сплошной системы (2 стержня, закрепленные шарнирами и винтами, и диск), мысленно отбросим пол и заменим его действие вертикальным противодействием Rn и Rn(рис. Б).

кроме противодействия пола, к твердому полу применяется следующее systems. In свой вес Q, прикрепленный на петлях Rod вес штанги 2H, в центре диска. Координатные оси показаны на рисунке 2. формируются два уравнения. Сумма проекций всех параллельных сил в вертикальном направлении равна пуле 2Ф«,= РД + РБ-2П-合計=сумма моментов всех сил для точки Oi D равна нулю 2 «((F » y = Rn■BD — (2Л+ Q)=0.Когда вы решаете уравнение Эгида together.

It выглядит так РД = рН = р + г. Как и ожидалось, реакция ИОЛ равны друг другу. Далее мы учитываем равновесие грани, отбрасывая стержень и заменяя действие на диск реакцией N и, а также,^(рисунок C).Поскольку трения между диском и штангой уже не условный, Afj реакции и, соответственно, перпендикулярно стержней АВ и CD. В результате, Н \и/ V образуют угол, равный горизонтальному.

В дополнение к реакции, тяжести вопрос действует на диск, и линии действия всех 3 сил пересекаются в центре диска. Напишите уравнение равновесия для диска： Fkx = СП, потому что это-ни что а = 0,£fky по по = СП, грех + грех-М = 0 Если вы решите эти 2 уравнения together. It выглядит так Q. ЛТ = М = М = 2 греха」

Таким образом, реакция стержней равна друг другу, и это очевидно, но по соображениям симметрии. Затем рассмотрим 1 равновесие стержня, заменим работу пола на известную реакцию Rn p и заменим давление диска на обнаруженное значение N (рисунок D).кроме того, на стержень действуют следующие силы: натяжение нити s, величина которого неизвестна, реакция шарниров О, величина и направление которой неизвестны, 2 составляющие R0x и R0yf и число реакций, представленных весом стержня p на Rn и Nit.

Так как необходимо найти только натяжение нити, то по condition. It достаточно создать одно уравнение точки равновесия пуля будет равна сумме моментов всех сил относительно точки О. Отсюда 5 = Задача 1.32. Левин ли, прикрепленный к точке с B поголку, представляет собой черную дыру с 2 лучами (рис. а) CD.

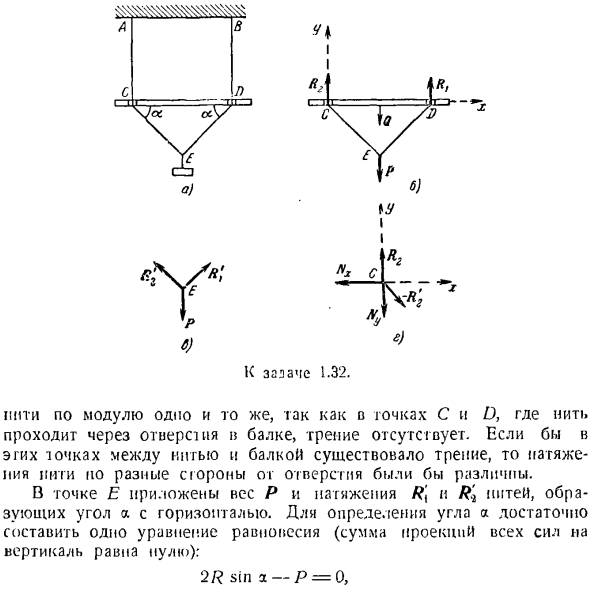
Нагрузка R суспендирована в середине винта P, и вес CD луча Q. расстояние луча AB. Предполагая, что балка и балка идеально гладкие, определяют угол α, образованный нижним участком балки и нитью в положении равновесия, натяжение нити и реакцию между балкой и нитью в точках C и D. The solution. To определите натяжение нити, мысленно перережьте AC и BD, учитывая равновесие нижней части системы (рисунок B）

Масса груза P, масса балки Q и резьбы R {и R + После того, как вы нарисовали координатные оси(рисунок B),.Создайте 2 уравнения равновесия = + = ТС МС(ФК)= РТ * компакт — (В + П)=0.Если вы решите эти 2 уравнения together. It выглядит так I,= = = 21 + 5.、 Однако,.Это видно из симметрии системы Чтобы найти угол a, рассмотрим баланс сил, приложенных к точке E (рисунок C).

Напряжение всех частей К моменту 1.32. Sui по модулю то же самое. Потому что нет трения для точек C и D, через которые нить проходит через отверстие в балке. Если существует трение в этих точках между резьбой и балкой, натяжение нити на разных сторонах отверстия будет различным. В точке Е вес нити, образующей горизонтальную линию, и угол a P, а также натяжение R1 и R’i равны applied.

To определив угол а, достаточно составить 1 уравнение равновесия (сумма проекций всех сил в вертикальном направлении равна нулю). ’2Р грех-П = О、

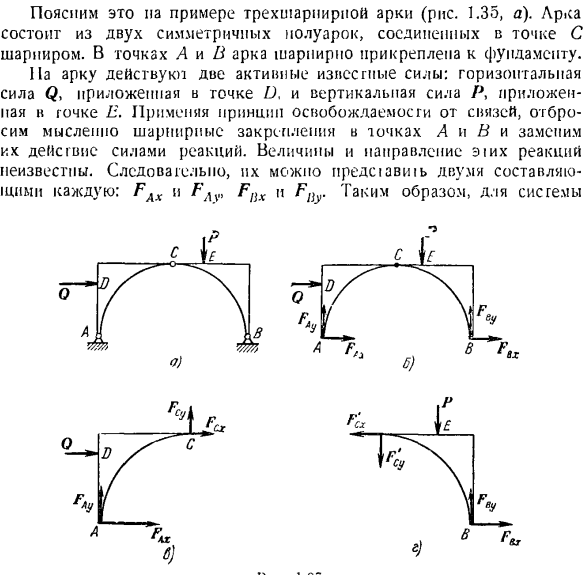
Позвольте мне объяснить это на примере 3 арки пищухи (рис. 1.35).Арка состоит из 2 симметричных половинных арок соединенных шарниром в точке C. At точки А и Б, арка шарпирио берет на фундамент. На арку действуют 2 активные известные силы: горизонтальная сила Q прикладывается к точке I, а вертикальная сила P>прикладывается к точке P. используя принцип высвобождения сустава, мысленно отбрасываем суставные сочленения точек A и B, заменяя их действия реактивной силой.

Величина и направление реакции золы неизвестны. Поэтому их предают 2 компонента (FAX и FAv, Flix и FBy) соответственно. Системы. •L 1 L » Твердое тело, которое отсасывает из 2 половинных дуг(рис. 1.35, 6), но может создать 3 уравнения равновесия. Однако число не подвешенных сил равно 4.Задача определяется как статически рассмотреть полудуговое равновесие (рис. 1.35, с).На левой половине арки есть 1 сила Q, и мысленно отбросьте петли A и C вместе с половиной арки на правой стороне.

Замените эти действия реакциями реакция в точке А представлена 2 компонентами F Ax и FAx, которые мы выбрали ранее. Величина и направление реакции в точке С также неизвестны. Компоненты FQx и FCy определяются уравнениями равновесия для левой половины дуги, но есть только 2 новых неизвестных. FCx и FCy. So, учитывая равновесие всей арки и левого нороака, существует 6 уравнений равновесия и 6 неизвестных.

То есть, проблема определяется статически. Та же задача. Рассмотрим равновесия левой половины дуги (рис.1.35, с) и равновесия правой половины дуги (рис. 1.35, Д) отдельно. Число уравнений равновесия в этом случае неизвестно, что можно решить другим способом (6).

Исходя из 5-го закона (закона действия и противодействия), компонент реакции шарнира Su, приложенный к правым полудугам F’qx, Fcy, равен по величине и направлен диаметрально противоположно соответствующему компоненту реакции того же шарнира C, который приложен к левым полудугам.

При решении задачи о твердом равновесии необходимо заполнить первые 4 пункта (15 страниц), которые указаны в начале book. In это дело,.Далее необходимо выделить твердые системы и отдельные твердые тела, которые являются частью системы： 5) сравните число неизвестных величин и число независимых уравнений равновесия. Если задачи определены статически, то эти числа должны быть равны. 6)самый удобный для you.

At то же самое время, для всех систем, в каждом теле и теле. Вы можете выбрать свою собственную систему координат 7) создать уравнения равновесия для каждого твердого тела или системы, в которой изучается равновесие. 8) решите систему уравнений равновесия сажи. Если систему твердых тел разделить на отдельные тела, заменив взаимодействие реакцией связывания, то введем реакцию, приложенную к 1 объекту и, исходя из закона уравнения действия и реакции, выберем реакцию, действующую на 2-й объект.

Например, рисунок 1.35, c и рисунок 1.35, Д). Если окажется, что величина неизвестной силы отрицательна в отклике, то направление этой силы следует принять в направлении, противоположном тому, которое показано на рисунке. При редактировании уравнений равновесия рекомендуется корректировать оси и точки, на которых редактируется уравнение момента силы так, чтобы каждое уравнение содержало только 1 неизвестную величину.

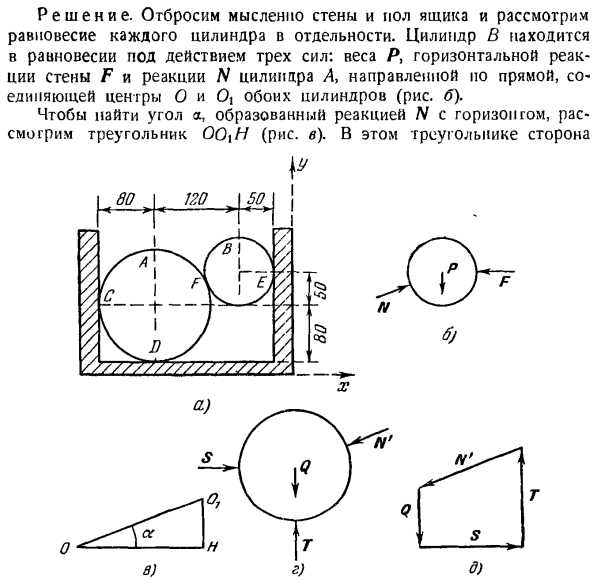
Если в силу условий задачи необходимо определить лишь несколько неизвестных величин, то необходимо составить только уравнения равновесия, необходимые для получения ответа. Задача 1.24. 2 гладких цилиндра A и B помещены в коробку(рисунок A).Вес цилиндра A равен Q = 40 кг, радиус R = 80 мм, а вес цилиндра B равен P = 30 кг, радиус R= 50 мм. Если ширина коробки составляет 250 мм, то определяют противодействие давления между вертикальными стенками точек С и Е, горизонтальной ИОЛ точки D и баллона.

Решение. Мысленно избавьтесь от стен и пола ящика. Рассмотрим баланс каждого цилиндра индивидуально цилиндр B находится в равновесии под действием 3 сил. Масса P, горизонтальная реактивная сила стенки F и реактивная сила N цилиндра a, направленная на прямую линию, соединяющую центр O и 0.

Оба цилиндра (рисунок b). Чтобы найти угол a, образованный реакцией N и горизонта, рассмотрим треугольник ООхН (рисунок C).По сторонам этого треугольника 00 / = Р +130 нога моя 0i = \ 20 используя теорему Пифагора, длина 2-й ноги 0j / 7 = 50.искать мм Вот так 5 12. Грех = ый, соѕ а = г^.

Так как линия действия силы, приложенной к цилиндру, пересекается с центром цилиндра, то достаточно создать 2 уравнения, которые устанавливают сумму проекций всех сил на оси x и y в ноль (рисунок а).）： £FkX = НКО * — Р = 0, ФКВ = Н грех <л-0

Смотрите также:

Предмет теоретическая механика

Система сходящихся сил	Равновесие тел при наличии трения
Произвольная плоская система сил. Случай параллельных сил	Графическая статистика и методы расчета ферм