Равносильность и следствие. Определение равносильности и следствия
Пусть даны два уравнения:

Уравнения (1) и (2) называются равносильными, если каждое решение уравнения (1) является решением уравнения (2) и, наоборот, каждое решение уравнения (2) является решением уравнения (1). Обозначение:
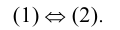
Иными словами, два уравнения равносильны, если множества их решений совпадают. Два уравнения, не имеющие решений, принято считать равносильными. Если одно уравнение не имеет решений, а другое имеет хотя бы одно решение, то в этом случае иногда считают, что второе уравнение является следствием первого (существуют и другие точки зрения на последний из указанных фактов [25]). Замена уравнения равносильным ему уравнением называется равносильным переходом.
Существует понятие равносильности на множестве. При этом уравнения могут не быть равносильными, но быть равносильными на некотором множестве. Например, уравнения 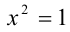 и
и 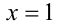 равносильны на множестве положительных чисел, а уравнения
равносильны на множестве положительных чисел, а уравнения 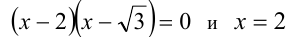 равносильны на множестве рациональных чисел.
равносильны на множестве рациональных чисел.
Если все решения уравнения (1) являются решениями уравнения (2), то последнее уравнение называют следствием уравнения (1) и обозначают:
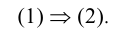
Следствие помимо корней исходного уравнения содержит обычно и другие (посторонние) решения. Поэтому если в процессе решения был осуществлен переход к следствию, то в конце решения задачи необходимо сделать проверку найденных значений неизвестной x для исключения посторонних корней. Используя понятие следствия, можно сформулировать определение равносильности уравнений (1) и (2) следующим образом: уравнения (1) и (2) равносильны, если
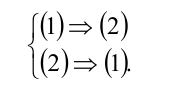
Заметим, что приведённые выше определения равносильности и следствия можно распространить на случай неравенств, а также систем и совокупностей.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

