Оглавление:







Равномерная сходимость функциональных последовательностей
Равномерная сходимость функциональных последовательностей. Определение 5.Учитывая последовательность функций (36.1) и функцию/, определяемую множеством Å, эта последовательность говорит, что в случае e функции сходятся равномерно/в множестве. В случае 0 n5 / ge существует число ne, которое становится неравенством Последовательность (36.1)называется сходящейся равномерно к множеству E, если существует функция/, сходящаяся равномерно к E. Очевидно, что если последовательность (36.1) сходится равномерно к функции! В множестве E он просто сходится к этой функции E. Если последовательность сходится к функции/в множестве E, мы описываем ее символически следующим образом.
Суть равномерной сходимости последовательности функций состоит в том, что для любого ε0 можно выделить номер, зависящий только от заданной ε и не зависящих от выбора точки x. Людмила Фирмаль
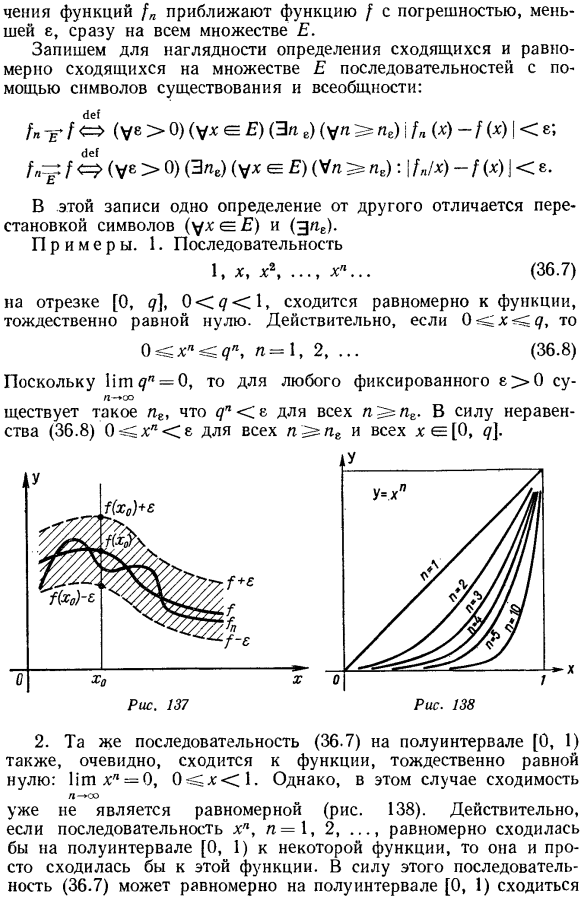
- Если эта последовательность сходится равномерно к функции/с E, то она описывается следующим образом: Заметим, что если последовательность (36.1) просто сходится к функции/множества, то это означает, что для любого ε0 и любого xe E существует число n0-in (e’, x), которое зависит как от e, так и от e из x, так что N> n0 неравенства (36.6) формируются для всех чисел. xeE.η> нэ неравенства (36.6), т. е.»график»функции помещается в»е-газа«, окружающей график функции} (рис. 137).
- Таким образом, для равномерной сходимости e 0 для всех N достаточно больших (т. е. n> n), значение функции fn аппроксимирует функцию f с ошибкой меньше e через множество E. ДВ этой записи определение 1 зависит от перестановки символов(для 1YEO) и (для zpE). Образцы. 1.Последовательность Интервал[0, 7], 0! 7; 1, сходятся равномерно к функции, равной zero. In факт, 0.если x s; 7, то ш7 7 «= 0, поэтому фиксированное ε0 DN для всех ЕТА не. есть такой нэ вроде r.
ля уточнения мы используем символы существования и универсальности для описания определения последовательности, сходящейся к множеству E и сходящейся равномерно. Людмила Фирмаль
- By неравенство (36.8), все η5 e. 2.Та же последовательность полуинтервалов[0, 1) (36.7) также сходится к функции, которая очевидно равна нулю. Птхл = 0, 0 ^ X1.Однако, в этом случае сходимость Неравномерно (рис.138). фактически последовательность xn, n = 1, 2,…Если, сходятся равномерно к функции, которая является полуинтервалом[0, 1), просто сходятся к этой функции. Это позволяет последовательности (36.7) сходиться равномерно к полупериоду[0, 1). Только функции, равные нулю во всех точках этого полусечения. Обратите внимание, что для фиксированного положительного целого числа n, Ptnl = 1.Таким образом, e, 0 e 1、 Для фиксированных n, xE, 0 xr! Существует 1, x » n0 и всех x∈E. И так оно и есть.
Смотрите также:

