Оглавление:
Рациональные уравнения
Квадратные уравнения.
Уравнение
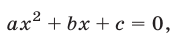
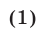
где а, b, с— заданные действительные числа,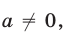 
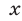— неизвестное, называют квадратным.
Приведем основные утверждения (теоремы), связанные с корнями квадратного уравнения (1).
1°. Квадратное уравнение (1):
а) имеет два действительных и различных корня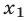 
и 
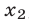, определенных по формулам
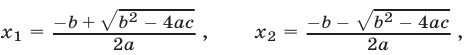
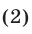
если дискриминант D квадратного уравнения (1) положителен, т. е.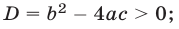 
б) имеет единственный корень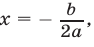 
если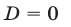 
;
в) не имеет действительных корней, если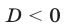 
.
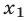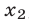2°. Теорема Виета. Если и — корни квадратного уравнения (1), то
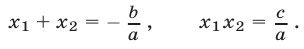
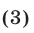
Для приведенного квадратного уравнения
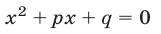
формулы Виета (3) принимают вид
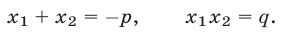
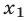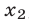3°. Если и — корни квадратного уравнения (1), то для любого 
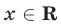справедливо равенство
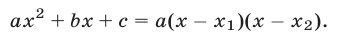
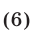
При выводе формул (2) используется метод выделения полного квадрата, т. е. следующее преобразование квадратного трехчлена
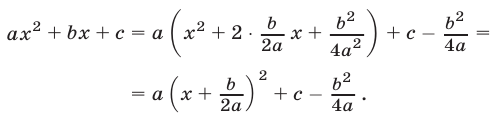
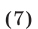
Равенство (7) можно записать в виде
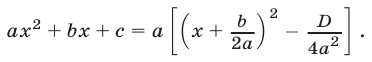
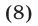
Формулы Виета (3) следуют из равенств (2), а для доказательства тождества (6) достаточно преобразовать его правую часть, используя (3).
Справедливо утверждение, обратное утверждению 1°.
4°. Если квадратное уравнение (1) имеет два действительных и различных корня, то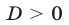 
; если уравнение (1) имеет единственный корень, то 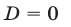; если уравнение (1) не имеет действительных корней, то .
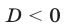Используя термины «необходимость» и «достаточность», можно объединить теоремы 1° и 4° и сформулировать следующее утверждение: для того чтобы квадратное уравнение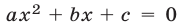 
имело два действительных различных корня, имело один действительный корень, не имело действительных корней, необходимо и достаточно выполнение соответственно условий 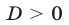, , 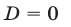, 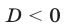где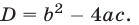 
Замечание. Если а, b, с — действительные числа,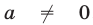 
, 
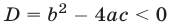, то многочлен второй степени (квадратный трехчлен) 
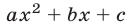имеет комплексные корни. Например, многочлен 
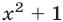имеет корни 
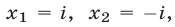т. е. 
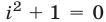и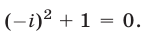 
В дальнейшем при решении уравнений и систем уравнений условимся ограничиваться отысканием только действительных решений и утверждение «уравнение не имеет корней» понимать так: «уравнение не имеет действительных корней».
При решении некоторых задач удобно пользоваться утверждением :
5°. Обратная теорема Виета: если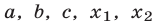 
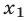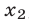— такие числа, что справедливы равенства (3), то и — корни квадратного уравнения (1).
Утверждение 4° можно доказать, используя метод доказательства от противного и утверждение 1°, а справедливость теоремы, обратной теореме Виета, следует из равенства (6).
Уравнения, сводящиеся к квадратным.
Биквадратное уравнение, т. е. уравнение вида
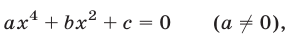
сводится к квадратному заменой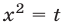 
.
К квадратному уравнению сводится уравнение вида
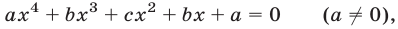
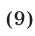
которое называют возвратным.
Заметим, что число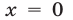 
не является корнем уравнения (9), поскольку 
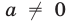. Следовательно, разделив обе его части на 
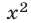, получим уравнение
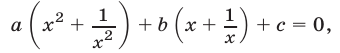
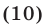
равносильное исходному. Сведем уравнение (10) к квадратному, полагая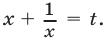 
Так как 
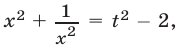то получаем квадратное уравнение
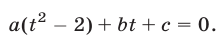
Корни многочлена.
Приведем некоторые сведения о корнях многочленов. Пусть задан многочлен n-й степени
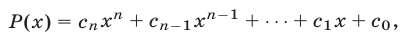
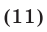
где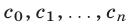 
—действительные числа,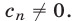 
Число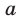 
называют корнем многочлена 
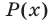, если 
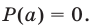Разделить многочлен 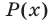на двучлен 
, где 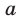— заданное число, означает представить его в виде
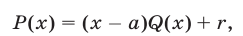
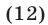
где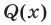 
— многочлен степени 
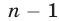, а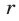 
—некоторое число (его называют остатком от деления многочле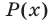на на ). Если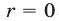 
, то говорят, что многочлен 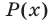делится без остатка (нацело) на .
Теорема Безу. Число 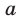является корнем многочлена 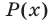тогда и только тогда, когда этот многочлен делится без остатка на , т.е. справедливо равенство
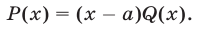
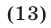
Доказательство. Если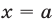 
— корень многочлена 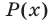, то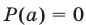 
. С другой стороны, из равенства (12) при 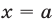получаем 
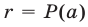. Следовательно, 
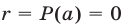, т. е. многочлен делится без остатка на . Это означает, что справедливо равенство (13).
Обратно, если многочлен 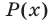делится без остатка на, т. е. справедливо равенство (13), то из этого равенства следует, что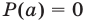 
, т. е. 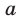— корень многочлена .
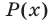Замечание. Для нахождения коэффициентов многочлена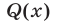 
можно либо использовать алгоритм деления многочлена на многочлен, либо приравнять коэффициенты при одинаковых степенях в равенстве (12) (или в равенстве (13), если 
).
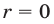Пусть коэффициенты многочлена 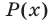являются целыми числами и пусть целое число 
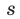является корнем этого многочлена, т.е. 
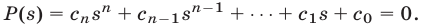Отсюда находим, что 
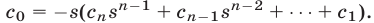Так как число, стоящее в скобках, является целым, то 
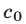делится на .
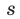Таким образом, целый корень многочлена с целыми коэффициентами является делителем свободного члена этого многочлена.
Корни рационального уравнения.
Рациональным называют уравнение вида
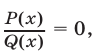
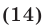
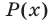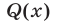где и — многочлены, причем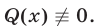 
Корнями уравнения (14) являются все те и только те корни уравнения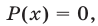 
которые удовлетворяют условию 
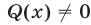. Иначе говоря, уравнение (1) равносильно системе
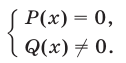
Примеры с решениями
Пример №70.
Пусть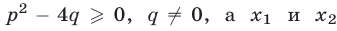 
— корни квадратного уравнения (4). Выразить через p и q следующие суммы:
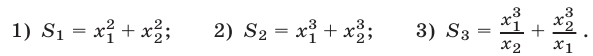
Решение:
1) Используя тождество
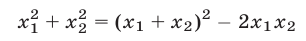
и формулы (5), получаем
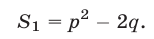
2) Применяя формулу для суммы кубов, находим
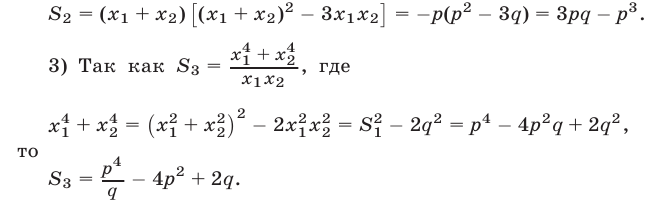
Пример №71.
Сократить дробь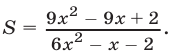 
Решение:
Применив формулы (2), найдем корн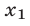и 
и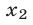 
квадратного уравнения 
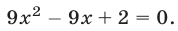Имеем
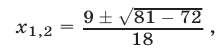
откуда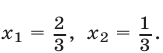 
По теореме 3° (формула (6)) получаем
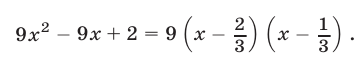
Аналогично, решив уравнение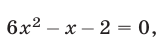 
находим его корн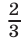и 
и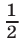 
; поэтому
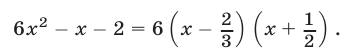
Итак,
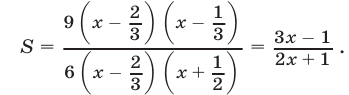
Пример №72.
Найти все значения 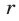, при которых уравнение
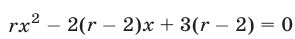
имеет один корень.
Решение:
Если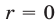
, то уравнение имеет один корень 
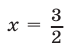. Если же 
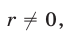то уравнение является квадратным и имеет один корень тогда и только тогда, когда его дискриминант 
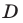равен нулю, т. е.
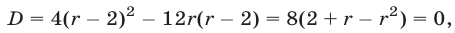
откуда находим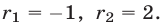 
Ответ.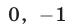 
и 
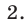
Пример №73.
Решить уравнение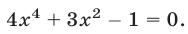 
Решение:
Полагая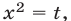 
получаем уравнение 
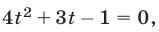имеющее корни 
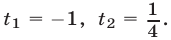Если 
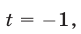то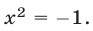 
Это уравнение не имеет действительных корней. Если 
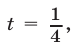то 
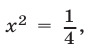откуда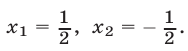 
Ответ.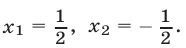 
53 = P—4p2 + 2 q.
Пример №74.
Решить уравнение
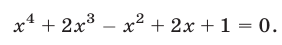
Решение:
Разделив обе части уравнения на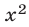 
, запишем его в виде
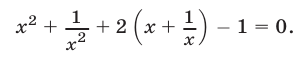
Полагая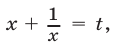 
получаем уравнение 
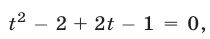откуда находим 
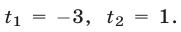Следовательно, исходное уравнение равносильно совокупности уравнений 
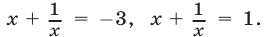Первое из них равносильно уравнению 
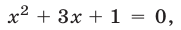имеющему корни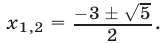 
Второе уравнение не имеет действительных корней.
Ответ.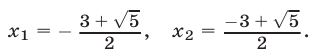 
Пример №75.
Решить уравнение
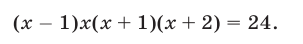
Решение:
Так как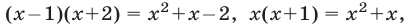 
то, полагая 
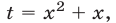приходим к уравнению 
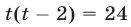или 
Это уравнение имеет корни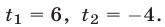 
Если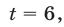 
то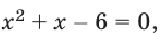 
откуда 
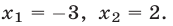Если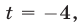 
то получаем уравнение 
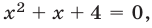не имеющее действительных корней.
Ответ.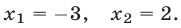 
Пример №76.
Решить уравнение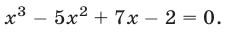 
Решение:
Целыми корнями многочлена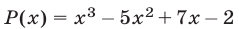 
могут быть только делители числа 
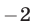, т. е. числа 
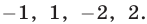Так как 
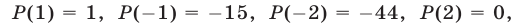то число 
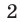— корень многочлена 
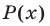и по теореме Безу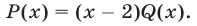 
Чтобы найти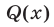 
, можно воспользоваться любым из способов, указанных в замечании. Укажем еще один способ отыскания 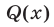, основанный на представлении многочлена 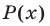в виде произведения двух множителей, один из которых равен 
. Так как
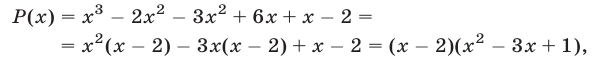
то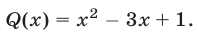 
Многочлен 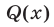имеет корни 
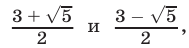являющиеся корнями исходного уравнения.
Ответ,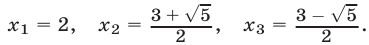 
Пример №77.
Решить уравнение
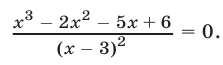
Решение:
Число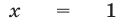 
является корнем многочлена 
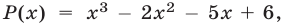так как 
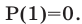Разложим многочлен 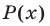на множители, для чего выделим множитель 
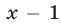. Тогда получим
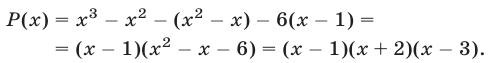
Следовательно, многочлен 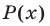имеет корни 
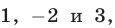из которых первые два удовлетворяют условию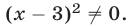 
Ответ.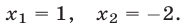 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Числовые неравенства примеры с решением |
| Уравнение и его корни. Преобразование уравнений |
| Иррациональные уравнения примеры с решением |
| Показательные уравнения примеры с решением |
