Рациональные сечения при изгибе
Определим рациональные сечения при изгибе, для этого сравним моменты сопротивления простейших сечений.
Осевой момент инерции прямоугольника (рис. 32.4, вывод формулы в лекции 25) равен
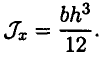

Осевой момент сопротивления прямоугольника
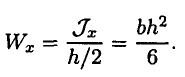
Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).
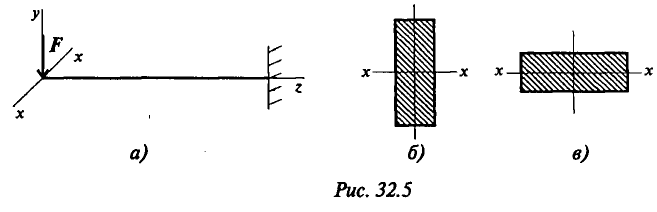
Вариант на рис. 32.56 обладает большим сопротивлением изгибу при прочих равных условиях.
Осевой момент инерции круга (рис. 32.6) равен
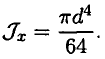
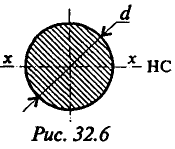
Осевой момент сопротивления круга
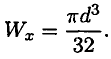
Все необходимые расчетные данные (площади, моменты инерции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1).
Для материалов, одинаково работающих на растяжение и сжатие, выбирают сечения, симметричные относительно оси, вокруг которой совершается изгиб (рис. 32.7).
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
| Деформации при чистом изгибе |
| Формула для расчета нормальных напряжений при изгибе |
| Поперечный изгиб. Внутренние силовые факторы |
| Понятия о линейных и угловых перемещениях при изгибе |
