Оглавление:
Рациональные неравенства, решаемые на отдельных промежутках ОДЗ
Иногда для решения задачи бывает удобно разбить ОДЗ на отдельные промежутки и на каждом из них решить задачу.
Пример №218.
Решить неравенство
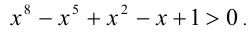
Решение:
Разобьём ОДЗ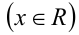 
на отдельные промежутки, и на каждом из них решим неравенство.
1) Пусть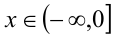 
. Оценим, какие значения при таких x принимает левая часть неравенства. Сгруппируем слагаемые:
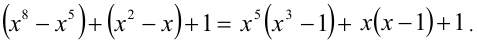
Первые два слагаемых неотрицательны, а третье — положительно, поэтому их сумма положительна на всем рассматриваемом промежутке.
2) Пусть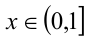 
. Оценим значения левой части неравенства при данных значениях x , по-другому сгруппировав слагаемые:
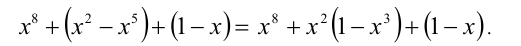
Первое слагаемое положительно, а два другие — неотрицательны, поэтому их сумма положительна на всем рассматриваемом промежутке.
3) Пусть, наконец,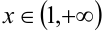 
. Тогда для удобства оценивания значений левой части неравенства сгруппируем слагаемые так же, как и в первом случае:
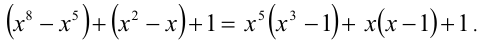
Эта сумма принимает положительные значения как сумма трёх положительных выражений.
Итак, мы доказали, что данное неравенство справедливо при всех действительных значениях переменной x. Ответ: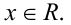 
Пример №219.
Решить неравенство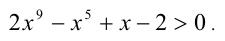 
Решение:
Разложим многочлен в левой части неравенства на множители: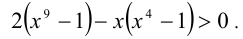 
Используя формулу разности n-х степеней
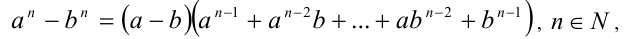
приведём неравенство к виду
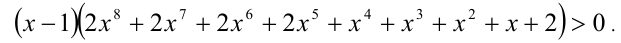
Обозначим выражение во вторых скобках через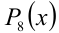 
и покажем, что этот многочлен принимает при всех x строго положительные значения. Для этого разобьём числовую ось на несколько промежутков, и на каждом из них, группируя слагаемые, добьёмся того, чтобы можно было легко оценить их знак.
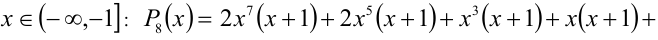
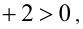, так как первые четыре слагаемых в этой сумме неотрицательны, а последнее — строго положительно.
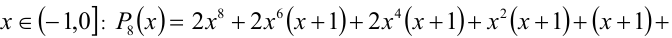
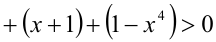
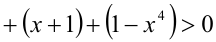, так как первые четыре слагаемых в этой сумме неотрицательны, а последние два — положительны.
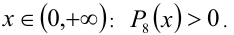
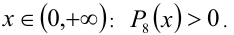Таким образом, поделив обе части решаемого неравенства на 
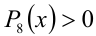, приходим к равносильному неравенству 
.
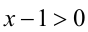Ответ: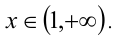
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
