Оглавление:
1.Рациональным алгебраическим уравнением с одним неизвестным x называется уравнение вида

где Р(х) и Q(x) — целые алгебраические многочлены.
В частности, если 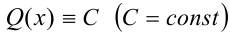 , то уравнение (1) превращается в целое рациональное уравнение. В общем случае, когда Q(x) — алгебраический многочлен ненулевой степени, имеем дробно-рациональное алгебраическое уравнение.
, то уравнение (1) превращается в целое рациональное уравнение. В общем случае, когда Q(x) — алгебраический многочлен ненулевой степени, имеем дробно-рациональное алгебраическое уравнение.
Если решаемое уравнение имеет вид
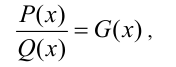
где G(x) — также некоторый алгебраический многочлен, то, как правило, его следует привести к виду (1) и уже затем решать:
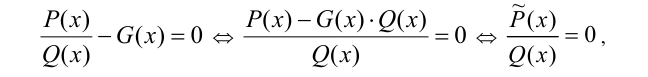
где 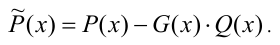
Основной метод решения дробно-рациональных уравнений состоит в том, что уравнение (1) сводится к равносильной ему системе, включающей целое алгебраическое уравнение и такого же вида неравенство:
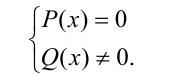
Так как решение дробно-рациональных алгебраических уравнений сводится в конечном счёте к решению целых уравнений, а основные способы решения последних уже рассматривались выше, то в данном пункте на решении рациональных уравнений мы подробно останавливаться не будем.
Пример №204.
Решить уравнение
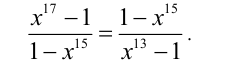
Решение:
Уравнение равносильно системе 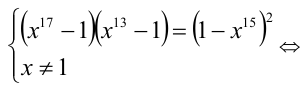
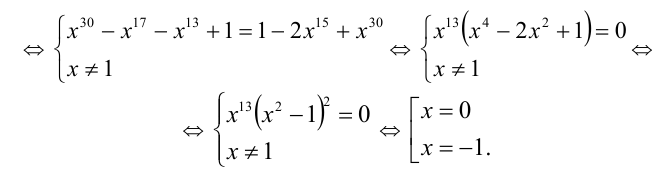
Пример №205.
Решить уравнение при всех действительных значениях параметра а :
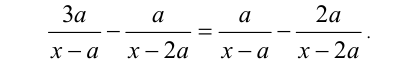
Решение:
Приведём подобные члены 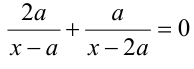 и затем приведём обе дроби к одному знаменателю:
и затем приведём обе дроби к одному знаменателю:
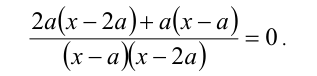
Полученное дробно-рациональное уравнение эквивалентно системе
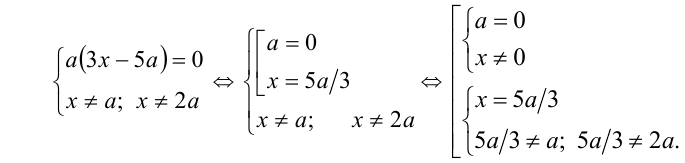
Ответ-, при 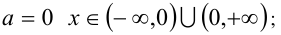 при
при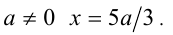
2.Неравенство одного из следующих видов
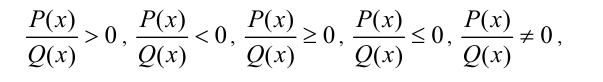
где Р(х) и Q(x) — целые алгебраические многочлены, называется рациональным (алгебраическим) неравенством.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

