Оглавление:
Расстояние от точки до прямой
Пусть имеем точку 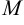
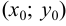 и прямую
и прямую 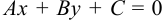 . Определим расстояние от точки
. Определим расстояние от точки 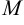 до этой прямой. Так как
до этой прямой. Так как 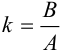 — коэффициент наклона прямой, проведенной через точку
— коэффициент наклона прямой, проведенной через точку 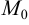 , то уравнение пучка прямых, проведенных через
, то уравнение пучка прямых, проведенных через 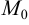 , имеет вид:
, имеет вид:
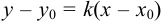 или
или 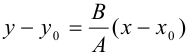 .
.
Отсюда 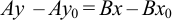 или
или 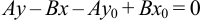 .
.
Получили систему линейных уравнений:
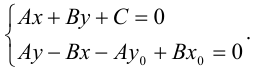
Ее решением является точка 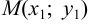 . Расстояние между точками
. Расстояние между точками 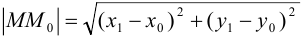 . Непосредственными вычислениями получаем
. Непосредственными вычислениями получаем
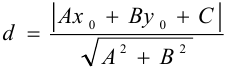 — расстояние от точки до прямой.
— расстояние от точки до прямой.
Задача №17.
Найти расстояние от точки (2; 1) до прямой 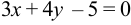 .
.
Решение:
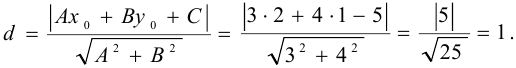
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Прямая на плоскости задача с решением |
| Угол между прямыми задача с решением |
| Решение задачи на треугольник |
| Векторы и операции над ними задачи с решением |

