Задача №37.
Рассмотрим задачу о равновесии системы, состоящей из шарнирного четырехзвенника 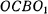 , к шарниру
, к шарниру 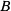 которого приложена вертикальная сила
которого приложена вертикальная сила 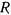 , а звено
, а звено  жестко связано с диском, центр которого находится в точке
жестко связано с диском, центр которого находится в точке 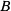 . К диску в точке
. К диску в точке 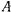 по касательной приложена горизонтальная сила
по касательной приложена горизонтальная сила 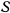 . Размеры в положении равновесия системы указаны на чертеже. Пренебрегая весом стержней и диска, а также трением в шарнирах, определить соотношение между величинами
. Размеры в положении равновесия системы указаны на чертеже. Пренебрегая весом стержней и диска, а также трением в шарнирах, определить соотношение между величинами 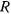 и
и 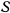 в положении равновесия, указанном на чертеже (рис. 30).
в положении равновесия, указанном на чертеже (рис. 30).

Решение:
Обе действующие на систему силы приложены к одному и тому же твердому телу, каким является диск. Мгновенное же движение диска сводится к одному повороту вокруг мгновенного центра вращения, который находится в точке 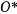 пересечения стержней
пересечения стержней 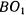 и
и 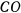 . Поэтому соответствующая этому возможному перемещению обобщенная сила
. Поэтому соответствующая этому возможному перемещению обобщенная сила  будет представлять собой сумму моментов действующих на систему активных сил относительно мгновенного центра вращения диска
будет представлять собой сумму моментов действующих на систему активных сил относительно мгновенного центра вращения диска 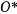 . Приравнивая нулю эту обобщенную силу, будем иметь
. Приравнивая нулю эту обобщенную силу, будем иметь
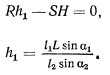
Отсюда сразу получаем условие равновесия в виде
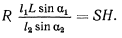
С задачей о равновесии системы материальных точек непосредственно связана и задача об устойчивости равновесия системы, когда на эту систему действуют только консервативные силы. Для тяжелых тел эта задача решается на основе принципа Торричелли, который устанавливает, что при устойчивом равновесии центр тяжести системы занимает наинизшее положение. Если ввести в рассмотрение силовую функцию
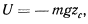
где 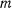 — масса всей системы, a
— масса всей системы, a  — вертикальная координата
— вертикальная координата  центра тяжести системы (ось
центра тяжести системы (ось  направлена вверх), то условие Торричелли сводится к нахождению максимума силовой функции.
направлена вверх), то условие Торричелли сводится к нахождению максимума силовой функции.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

