Задача №13.
Рассмотренный выше метод построения абсолютной скорости может быть применен для определения направления касательных к кривым, если иметь в виду, что вектор абсолютной скорости всегда направлен по касательной к траектории точки. Для определения направления абсолютной скорости движения материальной точки представляют как сумму двух более простых движений, направление которых известно. Пусть, например, требуется построить касательную к эллипсу.
Решение:
Эллипс -представляет собой геометрическое место точек, сумма расстояний которых до двух заданных центров (фокусов) является величиной постоянной:
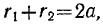
где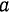 
— большая полуось эллипса. Выберем сначала подвижную систему осей 
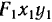с началом в фокусе 
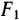направив ось 
в сторону движущейся по эллипсу точки 
(рис. 17). Тогда относительная точки равна скорости изменения расстояния от точки 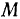до фокуса, то есть
Выберем теперь подвижную систему координат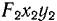 
с началом в фокусе 
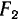направив ось 
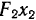в сторону движущейся точки 
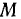. В новой системе координат относительная скорость точки 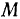направлена вдоль оси 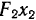а ее величина равна скорости изменения расстояния от точки 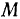до фокуса 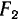то есть
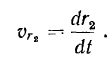
Из уравнения (а) имеем
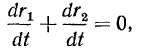
откуда
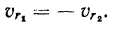
Обе подвижные системы имеют возможность только вращаться вокруг соответствующих фокусов. Благодаря этому и соответствующие переносные скорости направлены перпендикулярно к осям и 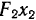. Па основании теоремы о сложении скоростей находим, что конец, вектора абсолютной скорости лежит на пересечении перпендикуляров к прямым и 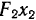, проведенным через концы соответствующих векторов относительной скорости.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
