Оглавление:
Рассмотрение уравнения относительного некоторой величины
Пусть имеется уравнение (неравенство), которое необходимо решить относительно неизвестной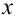 
. Если в уравнении имеется параметр, то в некоторых случаях такое уравнение удобно решать относительно параметра (или какой-либо другой величины). Наиболее часто среди задач этой группы встречаются задачи, решаемые как квадратные относительно параметра.
Пример №407.
Решить уравнение
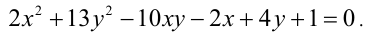
Решение:
Рассмотрим данное уравнение как квадратное относительно 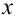. Приведя его к стандартному виду, получим
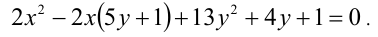
Чтобы уравнение имело решения, необходимо и достаточно, чтобы его дискриминант был неотрицателен:
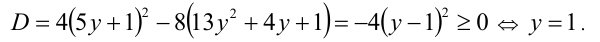
Тогда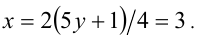 
Ответ: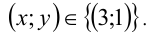 
.
Пример 2 . При каких значениях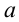 
уравнение 
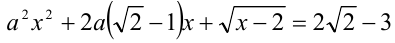имеет решения?
Решение:
ОДЗ: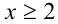
. Рассмотрим данное уравнение как квадратное относительно параметра 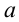. Приведём его к стандартному виду
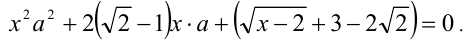
Квадратное уравнение (на ОДЗ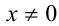 
) имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
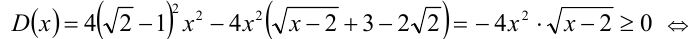
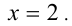Тогда, подставляя это значение 
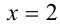в уравнение, получим 
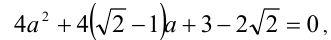откуда находим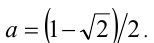
Замечание. Задачу можно было также решить, рассматривая данное уравнение как квадратное относительно выражения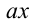 
.
Пример №408.
Найти множество значений функции
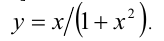
Решение:
Рассмотрим данное равенство, которое задаёт функцию, как алгебраическое уравнение относительно 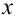с параметром 
. Преобразуем его к виду:
Сформулируем задачу в новой постановке: «При каких значениях 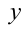уравнение (1) имеет решения?»
1) Если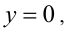 
то, подставляя в уравнение (1), находим 
.
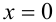2) Если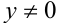 
(тогда и 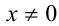), то уравнение является квадратным относительно 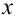, и оно будет иметь решения тогда и только тогда, когда его дискриминант неотрицателен:
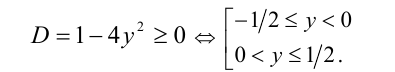
Объединяя все найденные значения 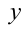, получаем:
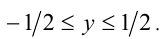Следовательно, множество значений функции представляет собой отрезок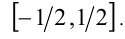 
Ответ: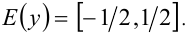
Пример №409.
Решить уравнение
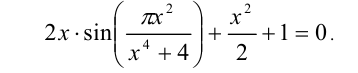
Решение:
Рассмотрим данное уравнение как квадратное относительно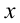
:
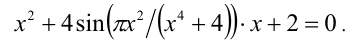
Необходимым и достаточным условием существования решений у этого уравнения является условие неотрицательности его дискриминанта:
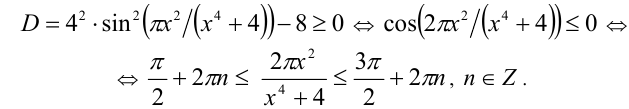
Оценим значения выражения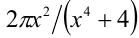 
, при помощи неравенства
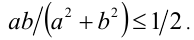Тогда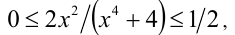 
и, значит, 
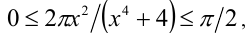следовательно, 
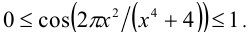Поэтому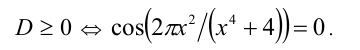
Отсюда находим
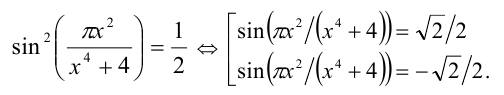
С учётом решаемого уравнения приходим к двум случаям:
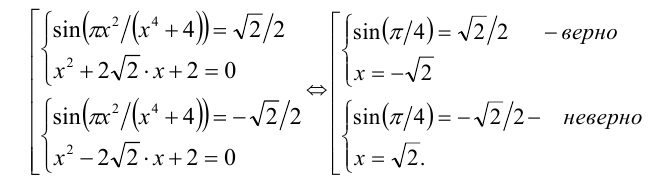
Ответ: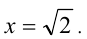 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
