Оглавление:
Рассмотрение уравнения относительно некоторой величины
Это известный алгебраический приём, когда уравнение (неравенство), решаемое в целых числах относительно одной величины (например, неизвестной x) бывает удобно рассмотреть относительно какой-либо иной величины (отличной от x). Так поступают в тех случаях, когда в новой формулировке задача оказывается в чём-то проще для решения. Чаще других встречаются задачи, где уравнение рассматривают как квадратное относительно параметра, одной из неизвестных (если в уравнении несколько неизвестных) или некоторого выражения. Обратимся к примерам.
Пример №64.
Решить в целых числах уравнение
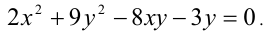
Решение:
Рассмотрим данное уравнение как квадратное относительно неизвестной x . Приведя его к стандартному виду, получаем
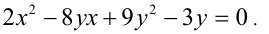
Необходимым и достаточным условием существования решений у этого уравнения является условие неотрицательности его дискриминанта:
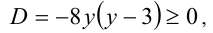
откуда находим ограничения на 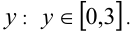 С учётом целочисленности у получаем, что
С учётом целочисленности у получаем, что 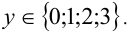 Рассмотрим каждый из случаев в отдельности.
Рассмотрим каждый из случаев в отдельности.
1) Если 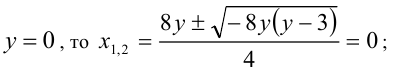
2) если 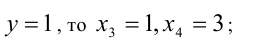
3) если 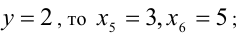
4) если 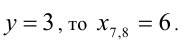
Ответ: 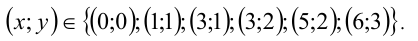
Пример №65.
Найти все целочисленные решения уравнения
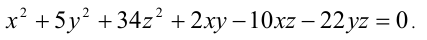
Решение:
1-й способ. Рассмотрим данное уравнение как квадратное относительно переменной x:
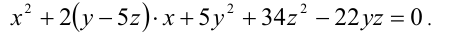
Дискриминант уравнения
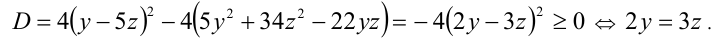
Тогда решением данного уравнения будет x =5z — у.
Итак, задача оказалась сведена к решению в целых числах системы
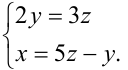
Заметим, что левая часть в уравнении 2у = 3z делится нацело на 2, следовательно, z должно быть кратно двум. Положим 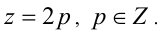 Подставляя в уравнение 2у = 3z, находим у = 3р , и тогда из второго уравнения системы получаем x =7р . Таким образом, решениями уравнения являются тройки чисел вида
Подставляя в уравнение 2у = 3z, находим у = 3р , и тогда из второго уравнения системы получаем x =7р . Таким образом, решениями уравнения являются тройки чисел вида 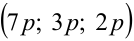 где
где 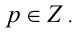
2-й способ. Задачу можно было решить иначе — при помощи выделения полных квадратов. Действительно, преобразуем уравнение к виду:
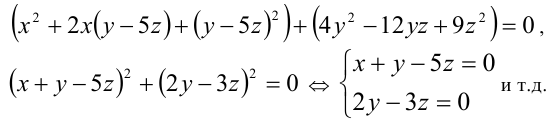
Ответ: 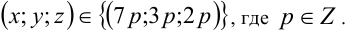
Пример №66.
Какое наибольшее число членов может содержать конечная арифметическая прогрессия с разностью 4 при условии, что квадрат её первого члена в сумме с остальными членами не превосходит 100?
Решение:
По условию имеем: 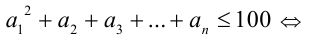
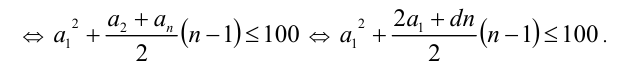
Рассмотрим данное неравенство как квадратное относительно 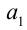 :
:
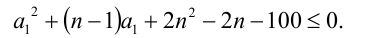
Для того чтобы это неравенство имело решения, необходимо и достаточно выполнения условия
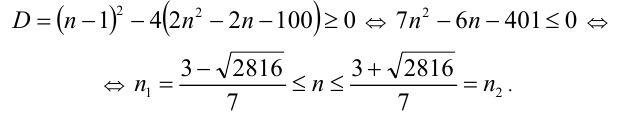
Так как 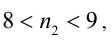 то наименьшее n равно 8.
то наименьшее n равно 8.
Ответ: 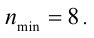
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

