Оглавление:




Рассеяние энергии при колебаниях
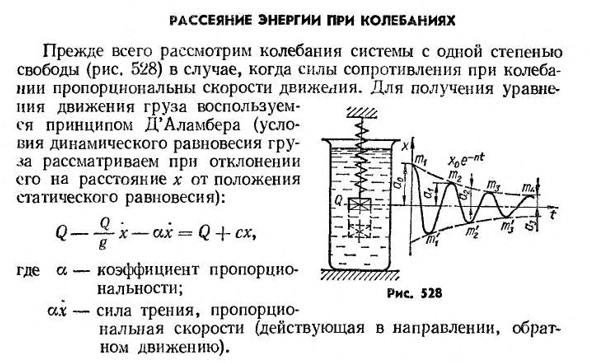
- Рассеивание энергии во время вибрации Сначала рассмотрим вибрацию системы с определенной степенью свободы(рис. 528), когда сила сопротивления вибрации пропорциональна скорости движения. Для получения уравнения движения груза мы используем принцип Д’Аламбера (учитывающий состояние динамического равновесия груза при отклонении расстояния x от положения статического
равновесия): Q — — — — — — — — x-Ah=Q+, Куда? — Рис пятьсот двадцать восемь Коэффициент пропорциональности; сила трения, пропорциональная скорости (действующая в противоположном направлении движения).Таким образом, дифференциальное уравнение колебаний системы с учетом диссипации энергии можно выразить следующим образом x4-2ph4-x2x=0, (20.25) Куда? У2=;2Р=. (20.26) Маркировка (20.27) Общее решение
дифференциального уравнения(20.25) может быть выражено в виде: х-э НТ (грех СО2 / Людмила Фирмаль
+в COS©,/), (20.28) Здесь e-2,718. Из этого уравнения следует, что период колебаний рассматриваемой системы с затуханием 2P_2l «G_ / co—p» ’(20.29), что зависит от затухания, характеризуемого коэффициентом p. Общее решение(20.28) является x=Me~n’Sin (JX/4-f), (20.30), где 31 и f-некоторые константы, зависящие от начальных условий и могут быть найдены таким же образом, как§ 124. В N co разность между круговой частотой (x) демпфирующей системы и собственной частотой co, то есть b=coj-I, является вторичным значением малости, поэтому период T почти равен периоду собственных колебаний. То есть можно считать, что малое
сопротивление не влияет на период (частоту) вибрации системы. Принимая во внимание решение(20.28), мы видим, что благодаря множителю e-nt амплитуда колебаний уменьшается со временем. Интегралы A и B констант, входящих в решение, определяются из начальных условий. Итак, предполагая первый момент (t=0) x=x0 и x-x0, получаем B=x0;a==-•(*(,+x0) из уравнения (20.28). В Формуле 542поставляя эти данные (20.28), получаем В частном случае, если A=0, то есть * 0/ПЦР(Ю. Последнее уравнение примет вид » =xt) e~’!потому что т о)/. (20.31)схематично соотношение (20.31) показано на рисунке. Уравнения для верхней и нижней огибающих приведенной
- демпфированной виброграммы 528 имеют вид X-XRF-NI и X = -HF-N соответственно. Точка Т?, госпожа.,.. Контакт огибающей с виброграммой имеет временную координату t-0;t-T; t-2T и др. И пункт ПК, В2, Т3,… Прикосновение к NIJ-T ZT Для огибающей кривой-координаты t= — y t= — y и т. д. В этом случае эти точки не совпадают с точкой крайнего смещения системы из положения равновесия. Из-за демпфирования системы переноса из среднего положения в следующее положение, время, необходимое для возврата следующих более высоких экстремумов положения, намного меньше этого. Степень демпфирования колебаний системы зависит от величины постоянной Р (демпфирующей характеристики).
Амплитуда колебаний после каждого цикла、 Как видно из уравнения(20.31), то есть уменьшение амплитуды соответствует геометрической прогрессии. Фактически, непрерывная амплитуда при t=0; t=G; t=2T и т. д. = = О Компании^» ^ 1 = = > ^ 2 = = W9 • » • » И так далее. Отношение амплитуды колебания к амплитуде непосредственно после него Откуда «о» 1.. . «фут=xtle~к» ТТ а я в Г1 мотыгой-(*+|, «г’ (20.32) Величина b называется логарифмическим затуханием затухания колебаний и обычно является основной характеристикой затухания колебаний. 543X В машиностроении, особенно в машиностроении, величина затухания существенно отличается от единицы, например, в вибрационной системе, такой как лопатка турбины, чем сила сопротивления пропорциональна скорости 0,03, то есть 3%, вибрация
(затухание) фактической структуры демпфирующей силы (демпфирование), Людмила Фирмаль
потери энергии в материале лопатки турбины. Другим распространенным источником потерь энергии при вибрации является сила трения стыков конструктивных элементов, диссипация энергии за счет утечки энергии в фундамент и др. Здесь мы работаем над расчетом вибрации элементов конструкции с учетом различных видов диссипации энергии 1, и только в случае вынужденной вибрации, когда диссипация энергии пропорциональна скорости.
Смотрите также:

