Оглавление:






Рассеяние частиц в физике
- Рассеяние частиц. Как упоминалось в предыдущем абзаце, полный Чтобы определить исход столкновения между двумя частицами (определить угол x), уравнение движения должно быть решено с учетом конкретного закона взаимодействия частиц.
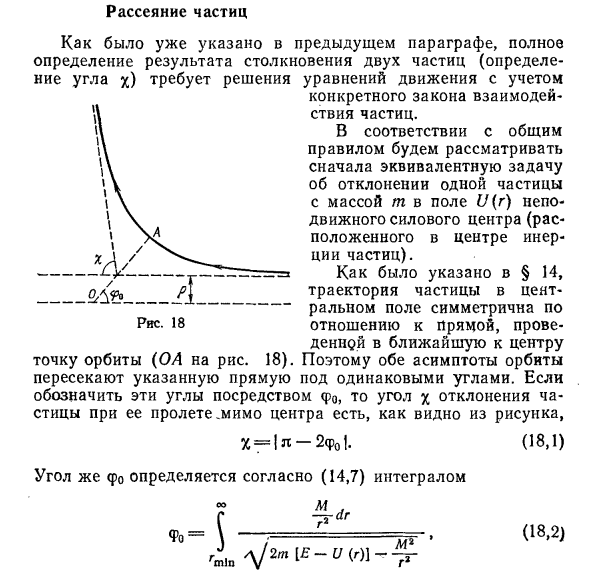
Рассмотрим сон в соответствии с общими правилами Эквивалентная проблема начала отклонять одну частицу с массой w в поле U (r) в центре силы, которая не движется (находится в центре инерции частицы).
Центральная полевая орбита частицы симметрична По отношению к линии Людмила Фирмаль
Как показано в §14, , ближайшей к центру Рисунок 18 Таким образом обе асимптоты траектории пересекают указанную линию Стирать под тем же углом. Если эти углы выражены как pho, угол отклонения x Как видно из диаграммы, X = | mr-2φ0 |. (18,1) Угол φ0 интегрируется в соответствии с (14.7) о (M / r-) * (182) J / 2 am [E-U (r) \ -M2 / r2 Взятый между местоположением, самым близким к центру и бесконечному расстоянию Положение частицы.
Напомним, что rm является корнем выражения под знаком радикала. Бесконечное движение, с которым мы имеем дело здесь, Вместо констант E и M-скорости v ^ удобно вводить другие вещи Частицы на бесконечности и так называемое расстояние столкновения р.
- Последняя длина перпендикуляра Расстояние, которое частица проходит через центр, когда она падает в направлении r ^ от центра, то есть, когда нет силового поля (рис. 18). Энергия и момент Эти значения E = M = mpv oo, (18,3) Выражение (18.2) принимает следующую форму: OO
а). Решения. Поскольку частицы могут свободно перемещаться за пределы шара и вообще не могут проникать внутрь шара, траектория состоит из двух линий, расположенных симметрично относительно нарисованного радиуса.
в системе C рассеяние является изотропным Людмила Фирмаль
До пересечения с мячом (рисунок 19). Как видно из рисунка, 7T-X p = грех (po = sin- Подставляя (18,7) или (18,8) в = cos-. 2 dA 710,2 • A 0,2 Aa = -inx dx = do, (1) Другими словами, . Интегрирование da по всем углам показывает, что полное поперечное сечение σ = pa2 в соответствии с тем фактом, что область удара, которая должна быть введена для рассеивания частиц вообще, является поперечным сечением шара.
Чтобы перейти к системе «l», необходимо выразить y в 01 согласно (17.4). Расчет полностью аналогичен расчету, выполненному в вопросе 2 §16 ( Формальное формальное сходство (17.4) и (16,5)). 77ii <777-2 (mi — масса частицы, 777-2 — масса шара) 2 jd o 1 = a— 4 2— ^ cos0i + 777-2 1 + (777-1 / 777-2) cos 201 д / л- (777-ф / 777-1) Sin2 01 Doi (Doi = 27t sin0i mp2vl0 (см. (14.11)), частица, которая «падает» в центре pmt = y / 2oc / mv%, не превышающий 0 Следовательно, желаемая эффективная площадь 2 2 полюса ®7TPh • mvle 5.
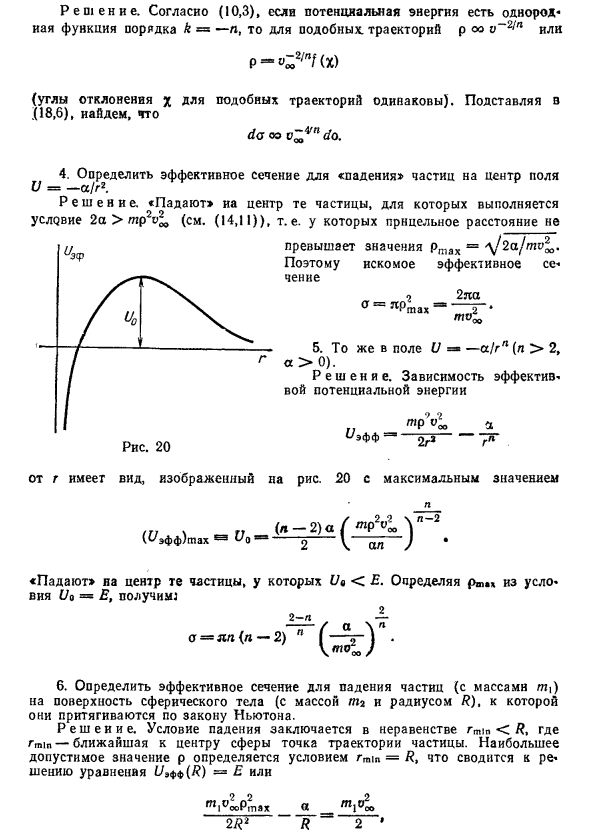
То же самое верно для поля U = —os / rn (n> 2, oc> 0). Решения. Эффективная зависимость от потенциальной энергии _ TR2U020 _ ef 2g2 gp Формат от r является максимальным значением на рисунке. п. (Tm \ -yy _ (n-2) a / m p Voc (C / eff) check = Uo —————— Uo (R) = E или TYll ^ oo Птах О.С. _ ТП \ В ^ 2R? R ~ 2 ’ Кроме того, σ = У1Ш2 2 (у — гравитационная постоянная), а мтм 1 принимается в предположении м2 м .
Найти здесь /? MAX5 В случае r ^ oo-V oo, эффективное сечение — это, естественно, геометрическая площадь сечения сферы. 7. Восстановить форму поля рассеяния U (r) по удельной зависимости эффективного сечения от угла рассеяния при удельной энергии E U (r) — монотонно убывающая функция от r (отталкивающее поле), и далее предполагается, что оно больше / (0)> E, U (oo) = 0 (О.Б. Фирсов, 1953).
Решения. d (Интеграл для угла рассеяния J определяется по формуле Do 2 -d X = 7rp (1) X Квадрат расстояния удара и, следовательно, функция p (x) (и вместе с ней x (p)) Вы также можете считать это дано. Вводим обозначения. / * =; • w = y1-! — (2) Далее выражения (18.1) и (18.2) можно записать в следующем формате: «O 71-х (ж) [дс 2 Дж г / х ш * -а * ‘ш о Где (х) — корень уравнения XW2 (так) -So = 0.
Уравнение (3) является интегральным уравнением для функции w (s) и может быть решено так же, как и в §12. SS OS S o (x) Rn-x (x) dx f f ds dxn-x (rd dx = r r J 2 года // ooss-хXJJ®оJ JуJ (xw2-s2) (oc-х) SO (a) SS так (l) f [dxds _ ^ [ds ) 0s (®0yj (xw2-s2) (oc-x) J w ′ Или интегрировать его в левую часть равенства, СС так (а) pu / os- [y / os-X ^ dx = 71 [-. J dx J w Ах ах
Различают взаимосвязь результатов по отношению к wass, а не после (oc) S en som meyan emaz note onneutstevtoos, s from sorp meship2 / 2 / w; n d {- \ — ^ d [-, -) [x ‘^ dx = —ds вес с2 / 2 / ш -nd \ nw = d (l) J 0 ВВ « У2 » Ф Это уравнение интегрируется напрямую. На правой стороне вам нужно изменить порядок интеграции dx и d (s / w). при s = 0 (т. е. r-oo) равно w = 1 (т. е. U = 0),
и когда мы вернемся к исходным переменным r и p, мы получим конечный результат (2) Эквивалентная форма): Oh Oh Oh w = exp {- [Arch- ■ ^ dp \ = exp {- [* (p) Φ1. (4) \ n j rw dp) {n J ^ p2 _ r2w 2 J RW RW Используя это выражение, зависимость w (r) (и, следовательно, U (r)) неявно определяется для всех r> rmin.
в области значения г Рассеянные частицы данной энергии Е фактически проходят когда мы вернемся к исходным переменным r и p, мы получим конечный результат (2) Эквивалентная форма): Oh Oh Oh w = exp {- [Arch- ■ ^ dp \ = exp {- [* (p) Φ1. (4) \ n j rw dp) {n J ^ p2 _ r2w 2 J RW RW Используя это выражение, зависимость w (r) (и, следовательно, U (r)) неявно определяется для всех r> rmin. в области значения г Рассеянные частицы данной энергии Е фактически проходят
Смотрите также:
| Распад частиц в физике | Формула Резерфорда |
| Упругие столкновения частиц в физике | Рассеяние под малыми углами в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

