Задача №164.
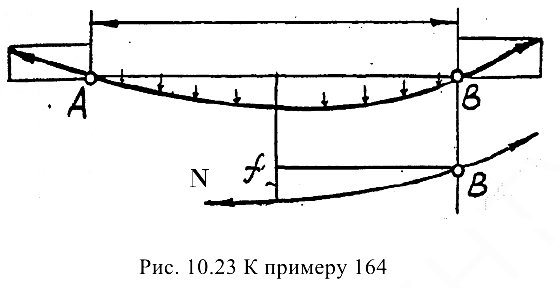
Рассчитать на прочность провод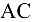 
(рис. 10.23), у которого длина 
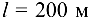, полная площадь сечения 
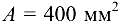, алюминиевая часть превосходит стальную в четыре раза; температура изменилась от 
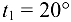до 
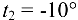; удельные приведенные нагрузки отличаются в 2,4 раза, рекомендуемый запас прочности 
.
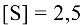Решение:
1. Составляем таблицы механических характеристик составных частей провода и исходных данных.
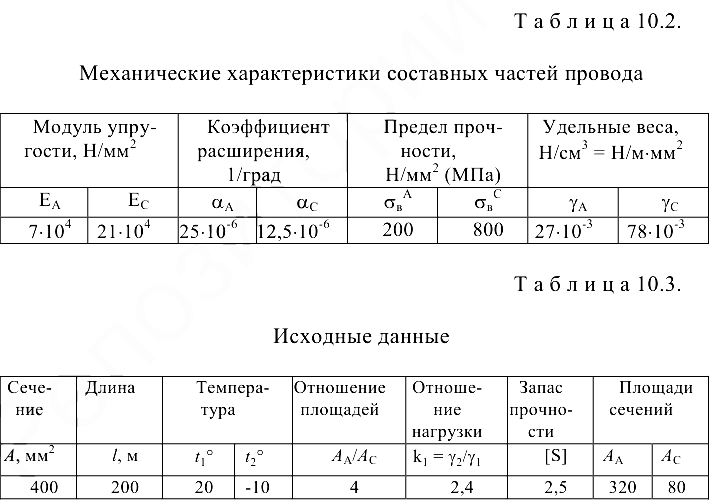
- Определяем приведенные величины биметаллического провода по формулам (10.7) — (10.10). Причем для ускорения вычислений
эти формулы следует упростить, разделив числители и знаменатели формул (10.7) — (10.9) на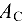
, а формулу (10.10) — на произведение 
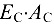и вводя при этом коэффициенты
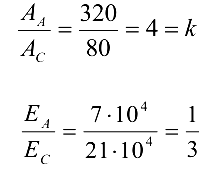
При вычислении приведенных величин особое внимание следует уделить их наименованию и размерностям
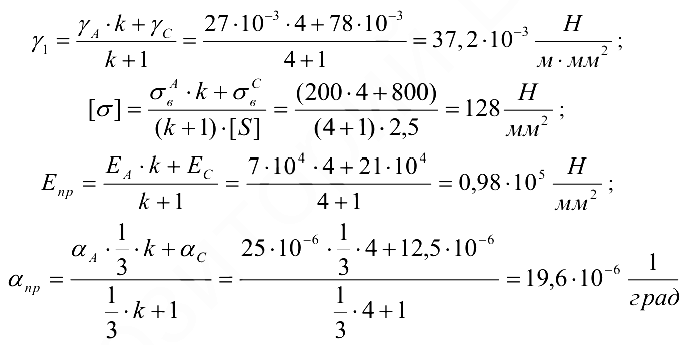
- По результатам приведенных величин и формулам (10.6), (10.5), (10.4), (10.3) последовательно получаем вспомогательные коэффициенты
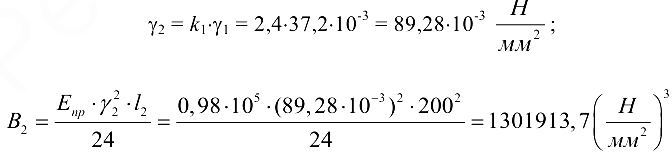
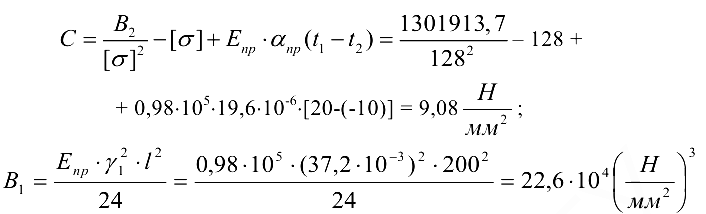
- По результатам расчетов приведенных величин составляем таблицу 10.4.
Найденные числа позволяют составить «уравнение состояния провода» (10.2):
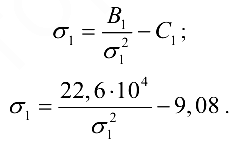
Решаем уравнение методом подбора или другим методом, приняв первую пробу
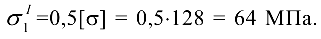
При подстановке оказывается, что это число не подходит. Вторая проба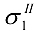 
= 55 МПа также не подходит, а 
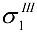= 58 МПа дает хорошее приближение. Окончательно 
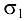= 58 МПа.
Определяем и анализируем результаты расчетов, которые сводим в таблицу (табл. 10.5).
Необходимая стела провисания:
летом
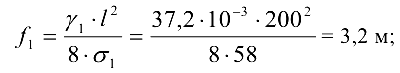
зимой
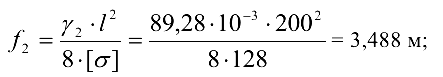
Близость результатов указывает на то, что зимняя нагрузка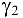 
скомпенсировала температурное укорочение провода. Летнее и зимнее «тяжение» провода:
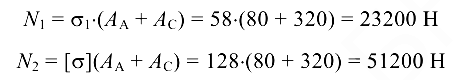
Очень важно вычислить и осмыслить распределение растягивающего усилия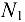 
и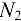 
по материалам провода (см. рис. 10.3, 10.4), т.е. в алюминиевой 
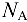и в стальной 
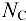частях. Из соотношения
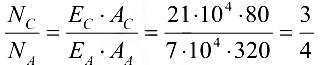
найдем 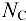и 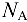в летний и зимний периоды:
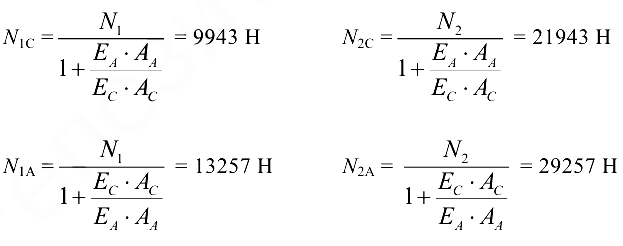
Усилия в алюминии и стали распределяются прямо пропорционально «жесткостям сечений», то есть произведениям площадей на модули упругости.
Выясняется, что растягивающие напряжения оказываются пропорциональными модулям упругости материалов независимо от площадей. Определим напряжения в частях биметаллического провода:
Оценка прочности частей биметаллического провода:
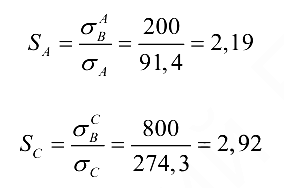
- Вывод: т.к.
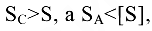, то это значит, что прочностных характеристик стали достаточно, а алюминия — недостаточно.
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
