Оглавление:

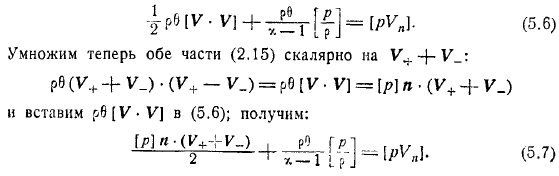
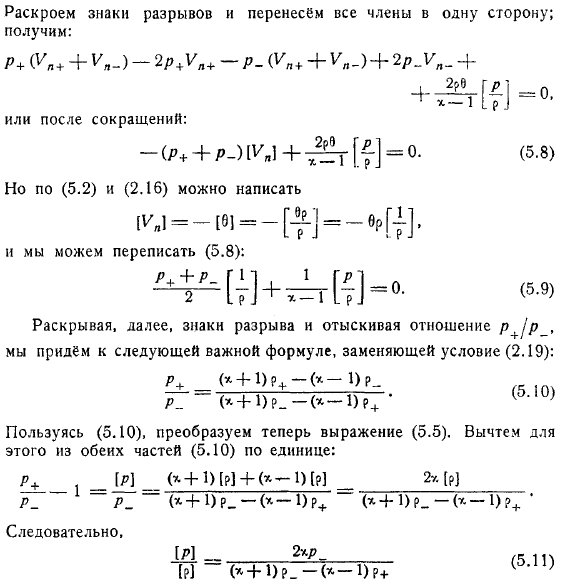
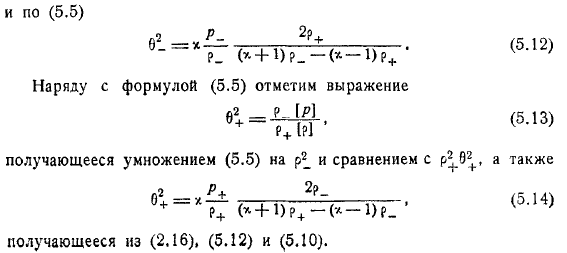




Распространение сильных разрывов. Теорема Цемплена
Чтобы найти скорость распространения сильного разрыва, мы сначала прибегаем к соотношению умножения скаляров. И обратите внимание на решение задач по гидромеханике, что для выражений, напишите. Вы можете написать его в следующей форме.
И мы можем узнать из отношений. Особенно очевидной становится разница между скоростью распространения слабого зазора, которая всегда равна, и формулой, полученной при преобразовании с использованием значимого результата соотношения. На что обратить внимание, сначала дайте характеристики уравнений газовой динамики и форму.
- Затем мы умножаем обе части на скаляр и вставляем его. Мы получаем. Выявить признаки разрыва и направить все члены в одном направлении.
- Мы получаем. Или после аббревиатуры. Но можно писать и переписывать.
Чтобы в дальнейшем выявить признаки разрыва и найти взаимосвязь, достигается следующая важная формула для замены условия. Людмила Фирмаль
Для этого нарисуйте единицу из обеих частей. С выражениями, будьте осторожны с выражениями.
Полученные путем умножения и сравнения. От формула показывает, что скорость распространения сильных разрывов всегда отличается от локальной скорости. Факт, согласно этим формулам, равенство. Или равенство. Он также включает в себя условия, но затем продолжается, и нет сильных пробелов.
- Если это так, или наоборот, это еще проще проверить. Если вы обратитесь к стационарным упражнениям, то получите очень значительное.
- Наименьшая односторонняя скорость разрывной поверхности превышает локальную скорость звука.
Поэтому стационарные поверхности с сильными разрывами и стационарными характеристиками могут существовать только при наличии сверхзвуковых скоростей. Докажем теорему зенфрена: возможны только сильные разрывы. Чтобы доказать это, необходимо использовать второй закон термодинамики.
Это не уменьшает энтропию во время физического процесса. Людмила Фирмаль
Энтропию можно представить в виде. Поэтому задача увеличения энтропии эквивалентна задаче увеличения размера. Поэтому значение не уменьшается.
Существует сильный разрыв в зыбкой. Определенная масса с одной стороны щели падает на другую сторону. Случая могут быть. В этом случае масса на положительной стороне разрыва плоской задачи функции становится отрицательной, а энтропия положительной области заменяется энтропией отрицательной области.
Потому что энтропия не уменьшается. И наоборот, если масса отрицательной области заменяется массой положительной стороны. Указывает, что это имеет место в обоих случаях. Факт, в итоге можно написать.
Легко видеть, что выражение в этой фигурной скобке является положительным и отрицательным. Поскольку они являются положительными, мы заключаем следующее. Доказана теорема земфрена.

