Производные сложных функций нескольких переменных

Распространение на случай функции от произвольной переменной

Распространение на случай функции от произвольной переменной. Опять же, мы будем говорить об общем случае. Здесь мы имеем в виду теорему, где переменная связана знаком равенства, неравенством или арифметической операцией, поэтому мы сначала имеем 2 или более функций f(x), # ^®,… (Определяется в той же области 5C) такими символами, это всегда означает, что эти значения соответствуют тем же значениям x. Все эти теоремы могут быть вновь доказаны аналогичным образом, как это было сделано в статье 37, но-это важно подчеркнуть-на самом деле нет абсолютно никакой необходимости доказывать их.

Говоря о границах функций, если принять во внимание «точку зрения последовательности», то доказывается теорема переменных, зависящих от указателя I, поэтому она применима и к функциям в общем случае. Людмила Фирмаль

• В качестве примера объясните теорему 1), 2), 3) из n°40. Предположим, что 2 функции f (x) и e (x) заданы в области 5C (точка конденсации a), и когда x переходит в a, оба имеют конечные пределы. ФМ Ф(Х)= а, FM F(х) б Затем функция Ф (Х)±B(Х), ф(х) е(х), (5） Есть также конечное ограничение(в некоторых случаях, предположим ВΦ0), т. е. A±B, A-B、 В «языке последовательности» эти отношения расшифровываются следующим образом: если {dgl [в последовательности (не-a) значений x, существует предел a、 /(Хп)->-а§(хп)-> Б Если вы примените доказанную теорему к этим 2 функциям из уже естественных аргументов, вы получите ее сразу. Hj.[/（））±^（■））] = А±Б, Э (хп)■е(хп)= а-б、 \ Тиэй = А В• И это (на»языке последовательности») выражает именно то, что должно быть доказано). /() б（*） *)В случае частного можно заметить, что x>достаточно близко к a (n * 40, как и в случае 3 yn).

По крайней мере, это имеет смысл. Потому что измеритель, дробь Эти х-значения. Аналогичным образом, общий случай, который мы рассматриваем в настоящее время, переносится на то, что было указано в§ 41 в отношении»неопределенного«, которое условно характеризуется символами О, Л. o> 55 ’0’°°>°°-°°Как и в простейшем случае, когда вы имели дело с функцией естественных аргументов, здесь недостаточно знать только пределы функций f (x)и^ (*), чтобы «раскрыть неопределенность», но следует также учитывать закон ее изменения. Примеры раскрытия неопределенности читатели найдут в следующем номере. Вернемся к этому вопросу в Главе VII главы 3, где показан общий метод раскрытия неопределенности с использованием дифференциального исчисления.

• Образцы. 1) пусть p (x) полиномиальное целое число О x с постоянными коэффициентами： р(х)= а, х » + a1xk-’+ … + Аляска.1х + АК(а » 0). поднимает вопрос о его пределах как g > + oo. Если все коэффициенты этого многочлена положительны (отрицательны), то вы сразу увидите, что предел p (x) равен+ oo (oo).Однако для коэффициентов различных кодов некоторые члены имеют тенденцию быть-{oo, другие имеют тенденцию быть-oo, и существует неопределенность в виде oo-oo. Чтобы выявить эту неопределенность, p (x)= x * [a> +〜+ … Представляет p (q) в виде (+^1 + p). Выражение в скобках имеет предел a0 ^ 0, потому что все члены в скобках, начиная со 2-го, бесконечно малы, а X увеличивается бесконечно. Первый фактор is—oo. In в этом случае все выражение будет+ oo или-oo в зависимости от знака a9. В частности, присвоение натурального числа n вместо непрерывно меняющейся переменной x дает тот же результат.

Читатель должен определить Ptp (t) как x °°(на этот раз мы будем рассматривать четность или нечетные числа показателей K). во всех случаях границы полинома p (q;) совпадают с границами его основного члена a0x. Устранение «неопределенности» путем преобразования этого выражения, используемого здесь, часто используется для выявления неопределенности. 2) Если^(x) тот же многочлен Я()= б «Х1 + а» 1 + … + b [_xx + b [(b» 0）、 П（） Тогда, Икс?(*) отношение как к 00 + co представляет собой неопределенность формы-. Да. Р(х） Я(x） = Х * −1. а°+%±+ п «О + ^ + … +％ Если вы преобразуете каждый полином таким же образом, как в Примере 1: ах8 Т. * o; = = и 1 ’+ 2 * + 2-й фактор здесь имеет конечный предел■ ФО. Обе степени о * Полином равен: d^=/, следовательно, предел отношения равен^.

Все случаи ограничения полиномиального отношения согласуются с ограничениями отношения старшего члена. Людмила Фирмаль

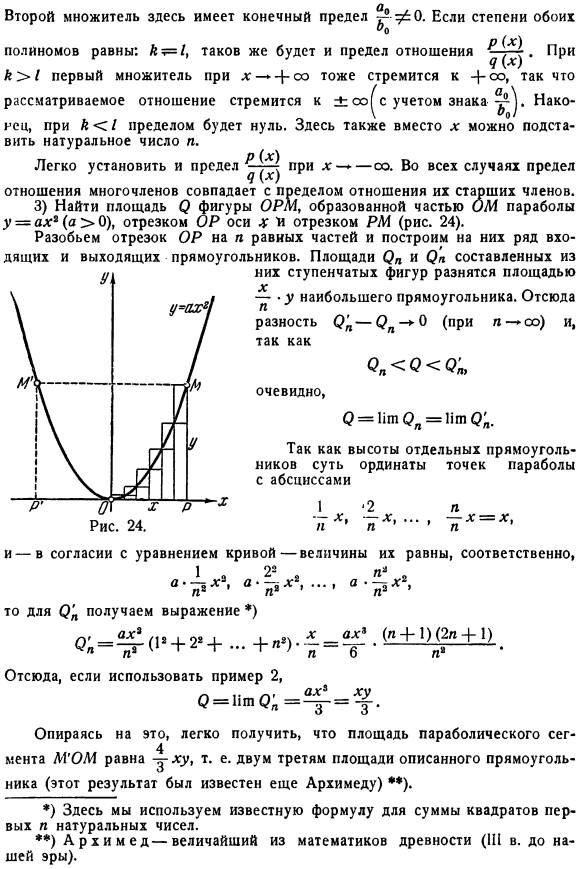
• In Первый фактор как A> / x * + co также имеет тенденцию быть -} oo Это неправда. * .Г Рассматриваемые соотношения имеют тенденцию быть±oo^, принимая во внимание символы ic, K / limit будет равен нулю. Здесь вместо x можно присвоить натуральное число n. Простота установки и ограничения Р(х） Я(x） x > co. In 3) найти площадь фигуры Φ ОРМ, образованный ом часть параболы топор *(а> 0), отрезок ОП оси, отрез РМ (рис. 24). Разделите отрезок OP на n равных частей и создайте на них ряд входящих и исходящих прямоугольников. Квадратные и операционные усилители, состоящие из Их диаграммы шагов различаются в зависимости от региона *С самым большим прямоугольником. Таким образом (β; 0 > 0 (для η-ω) и н * Р = НШ(?Н = ишо;. Так как высота отдельного прямоугольника является ординатой точек параболы.

Смотрите также:

Решение задач по математическому анализу

Арифметические операции над переменными.	Предел монотонной функции от натурального аргумента.
Неопределенные выражения.	Лемма о вложенных промежутках.