Распределённые силы
Ранее мы рассматривали действие на тело лишь сосредоточенных сил, сил приложенных к одной точке. Но можно привести ряд примеров, когда силы распределяются по всему объёму тела, по площади или по длине. Кстати, вес тела, сила тяжести, это тоже сила, распределённая по объёму тела. Потому что на каждую точку его действует сила, её вес. А при решении задач мы вес тела показываем в виде сосредоточенной силы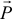 
, равнодействующей всех сил, приложенной к центру тяжести.
Можно встретить силы, распределённые по плоскости, по поверхности (например, снег, лежащий на крыше; давление газа или жидкости на поверхность сосуда). И силы, которые распределяются по линии.
Все эти распределённые силы характеризуются их интенсивностью -силой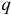 
, действующей на единицу объёма, площади или длины тела. Размерность интенсивности — 
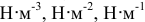соответственно.
Действие таких сил на тело заменяем одной силой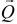 
, равнодействующей этих распределённых сил .
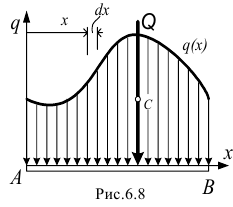
Проще всего определить её для параллельных сил, распределённых по длине, по прямой линии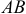 
(рис.6.8).
Выделим на расстоянии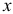 
участок линии длиной 
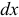. На этом участке на тело действует элементарная сила 
.
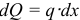И, интегрируя по всей длине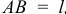 
, получим равнодействующую
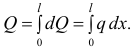
Значит, величина равнодействующей равна площади заключённой между линией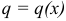 
и осью 
.
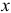Точку приложения силы 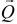или лучше линию действия её, можно найти с помощью теоремы Вариньона (5.8).
Момент равнодействующей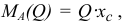 
, а сумма моментов элементарных сил 
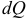относительно той же точки 
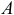равна
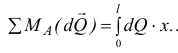
Приняв их, получим
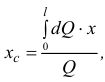
но по аналогичной формуле (6.4) определяется координата центра тяжести рассматриваемой площади. Значит, точка приложения силы 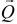к телу и линия действия её определяются центром тяжести этой площади.
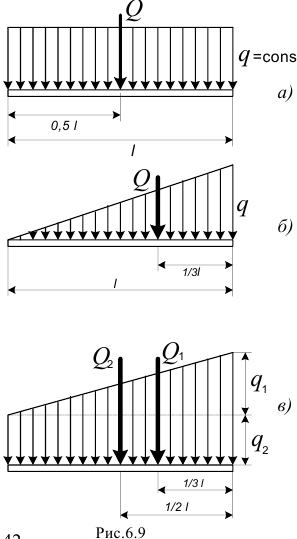
Если распределение нагрузки определяется линейным законом, модуль равнодействующей и линия действия её находятся довольно просто (рис. 6.9, а и 6).
А при распределении по закону трапеции (рис.6.9, в) её нужно разделить на треугольник и прямоугольник и находить соответственно две силы
Если сила распределена не по прямой линии, то равнодействующая находится немного сложнее, Например, при давлении жидкости или газа на внутреннюю стенку трубы в каком-нибудь её сечении.
Найдём равнодействующую такой распределённой силы на часть стенки трубы, которая определёна дугой с углом 
( рис. 6.10).
На участок дуги, определяемый углом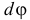 
, действует элементарная сила
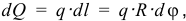
где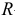 
— радиус дуги.
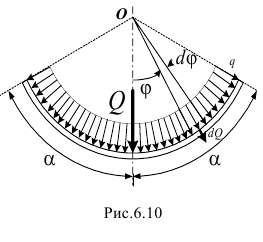
А на всю дугу действует равнодействующая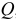 
, равная сумме проекций всех элементарных сил на вертикальную ось симметрии, то есть
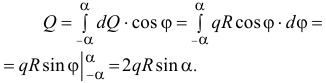
Так на половину трубы действует сила (при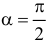 
), равная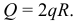 
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Сложение параллельных сил. Центр параллельных сил |
| Центр тяжести тел |
| Трение скольжения |
| Трение качения |
