Распределение ускорений в плоскопараллельном движении твердого тела

Распределение ускорений в плоскопараллельном движении твердого тела

Распределение ускорений

Плоскопараллельное движение является частным случаем движения твердого тела. На практике этот случай встречается наиболее часто, а потому и будет исследован особо. При изучении плоскопараллельного движения твердого тела, как это уже отмечалось выше, можно ограничиться рассмотрением движения некоторого плоского сечения твердого тела. Будем изучать движение плоского сечения по отношению к системе прямоугольных осей, которую будем считать неподвижной. 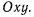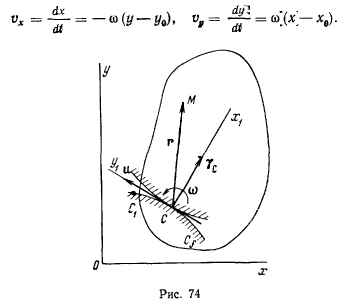Обозначим эту систему осей через Пусть мгновенный центр вращения твердого тела находится в точке 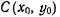Координаты произвольной точки М твердого тела обозначим через х и у. Скорости точек твердого тела определяются по формуле Эйлера

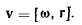
Откуда проекции скорости на неподвижные оси координат найдем
при помощи матрицы

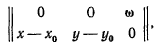
откуда имеем

Проекции ускорения точки М на неподвижные оси координат получим, дифференцируя по времени формулы для проекций скорости

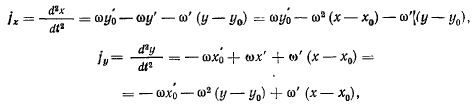
где величины 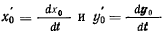представляют проекции на
неподвижные оси координат скорости движения по центроиде мгновенного центра вращения. Вектор 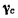с проекциями на неподвижные оси координат будет, очевидно, определять
ускорение точки С твердого тела (чтобы убедиться в этом, достаточно
в формулах для ускорений положить 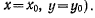Проекции этого
вектора можно найти из матрицы

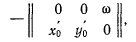
а сам вектор 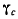можно определить формулой

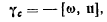
где 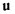— скорость движения мгновенного центра вращения по центроиде. Формула показывает, что ускорение точки С твердого тела направлено ортогонально к центроиде в сторону вращения. Это же можно получить и непосредственно. Выберем неподвижную систему осей так, чтобы ее начало совпадало в данный момент с точкой С, а ось 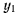была бы направлена в сторону направления скорости движения мгновенного центра вращения. Тогда для проекций скорости мгновенного центра вращения будем иметь

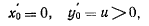
а для проекций вектора 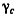получим значения

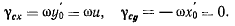
Если бы мгновенный центр вращения оставался неподвижным, т. е.
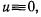то ускорения точек твердого тела определялись бы как
ускорения во вращательном движении твердого тела. При этом
касательное ускорение 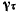и нормальное ускорение 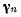можно задать
проекциями на неподвижные оси координат:

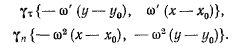
Здесь вектор 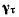направлен по скорости точки М, а вектор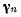
ортогонален к скорости. Формулы для определения ускорений точек
твердого тела можно представить в векторном виде

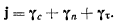
Полученная формула представляет собой одну из разновидностей выведенной выше формулы Ривальса, примененной для случая плоскопараллельного движения, в которой за полюс взят мгновенный центр вращения плоской фигуры. Если обозначить через r расстояние точки М от мгновенного центра вращения, то для определения величин касательного и нормального ускорений будем иметь

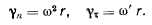
Замечание. К этим же результатам можно прийти непосредственно, исходя из теоремы о сложении ускорений для точки (теоремы Кориолиса), если за начало подвижной системы координат, движущейся поступательно, принять точку твердого тела, совпадающую в данный момент с мгновенным центром вращения. Тогда относительное ускорение точки М определится как ускорение точки в ее движении по окружности и будет складываться из

нормального и касательного ускорений. Переносным ускорением будет ускорение точки С. Добавочное ускорение здесь равно нулю, по-
поскольку подвижная система движется поступательно. Для определения переносного ускорения рассмотрим движение точки С по центроиде (рис. 74). Мгновенный центр вращения С за время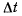
переместится в точку 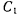и в момент 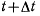твердое тело будет
вращаться вокруг точки 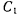с угловой скоростью 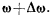Скорость
точки С будет направлена в сторону вращения, ортогонально к хорде
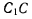и будет равна

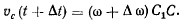
Модуль ускорения точки С по определению равен

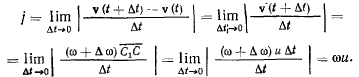
Пример:

Палочка АВ скользит своим концом А по окружности и
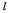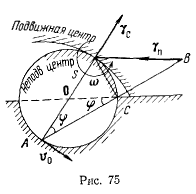
всегда проходит через точку С этой окружности. Определить ускорение точки В, расположенной на расстоянии от точки А, если последняя движется по окружности с постоянной скоростью 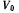(рис. 75).

Решение:

Мгновенный центр вращения палочки находится на пересечении диаметра окружности, проходящего через точку А, и перпендикуляра к палочке, восстановленного в точке С. Расстояние от Центра окружности до мгновенного центра вращения равно радиусу окружности, а неподвижной центроидой является сама окружность. Расстояние от точки А до мгновенного центра вращения равно диаметру окружности и остается постоянным. Под- Подвижной центроидой будет окружность диаметром 2r с центром в точке А палочки 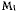иовеиная угловая скорость вращения палочки

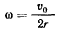
есть величина постоянная. Угловое ускорение 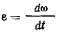равно нулю, а потому равно нулю и касательное ускорение 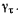Нормальное ускорение точки В

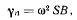
где

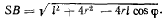
Ускорение точки, совпадающей с мгновенным центром вращения, равно

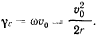
Проекция ускорения точки В на направление палочки

Пример:

Окружность радиуса r катится без скольжения по
неподвижному прямолинейному рельсу так, что скорость ее центра 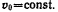Определить ускорение точки С окружности, касающейся в данный момент рельса (рис. 76).

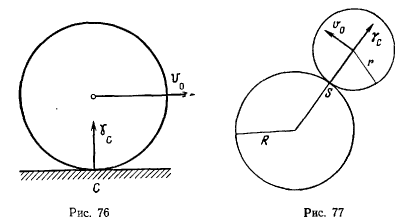
Решение:

Точка С является мгновенным центром вращения окружности. Скорость движения мгновенного центра равна 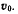Ускорение точки С окружности определяется из условия

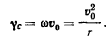
Пример:

Окружность радиуса r катится без скольжения по
неподвижной окружности радиуса R так, что скорость ее центра в данный момент равна 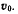Определить ускорение той точки подвижной окружности, которая в данный момент касается неподвижной окружности (рис. 77).

Решение:

Мгновенный центр вращения подвижной окружности находится в точке S соприкосновения двух окружностей. Мгновенная угловая скорость 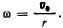Скорость движения мгновенного центра вращения по центроиде определится из соотношения

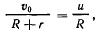
откуда

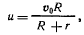
и ускорение точки твердого тела, совпадающей с его мгновенным центром вращения, получит вид

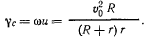
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Векторный вывод теоремы Кориолиса

Теорема Ривальса

Мгновенный центр ускорений

Кинематические уравнения эйлера