Распределение местных скоростей. Расход. Средняя скорость

Распределение местных скоростей. Расход. Средняя скорость

Распределение местных скоростей. Расход. Средняя скорость. Круглая цилиндрическая трубка. Локальное распределение скоростей. Рассмотрим движение равномерного ламинарного давления в цилиндрической трубе круглого сечения радиусом r0 (рис. 8.1). 146. Движение аксиально-симметрично. Такие перемещения рекомендуется рассматривать в системе координат (x, r), где ось OX ориентирована вдоль оси трубы. r-радиус точки поперечного сечения, перпендикулярной оси. Равномерное ламинарное движение потока в трубе Они-и; ИГ-0.(8.1） Тангенциальное напряжение, создаваемое между слоями жидкости Ньютоном[см. (1.12）] (8.2） АГ.

Поэтому распределение осредненных во времени местных скоростей по сечению оказывается здесь более равномерным, чем при ламинарном режиме. Людмила Фирмаль

• По мере увеличения r (от оси к стенке трубы) скорость u уменьшается. Поэтому наклон скорости ui равен r <. возможно ли это? Поскольку касательное напряжение m является положительной величиной, в (8.2) вводится знак минус. В случае напряжения сдвига соотношение(7.31) было получено ранее Где / гидравлический градиент. Ли. 2 г г. ’ (8.3)） Уравнение (7.31) и уравнение (8.2)、 Откуда? Йи ^ гыг ГИТ. 2К, 2У. 10. * 147. Предполагая, что V не изменяется в пределах живого поперечного сечения[UV} (g)] и / не зависит от g、 После интеграции И—Ха + С. IV.

Найти интегральную постоянную C от состояния, в котором жидкость «прилипает» к стенке. для r = r0 скорость u = 0; следовательно、 с = ^ Р1 Затем о локальной скорости в точке живого сечения на расстоянии r от оси трубы、 «=(8.4） Так, в случае движения ламинарного потока в цилиндрической трубе круглого сечения(напорный поток) распределение локальной скорости по радиусу имеет свойства параболы (рис.8.1).Скорость esolar-параболическая. Из (8.4) следует, что максимальная скорость возникает на оси трубы, то есть если r = 0 Два МТА » Иди. 4 \> Представление локальных скоростей через ITA\ «=»М» (Г / г0) 2]. (8.5） Безразмерная локальная скорость ^ ^Макс= 1 (р! Р0) (8.6).

• Таким образом, фигуры для безразмерной локальной скорости при ламинарном движении жидкости в трубе идентичны и могут быть представлены в виде парабол (8.6). Cost. To определить расход на 1 сечении трубы, выбрать кольцеобразную основную площадь толщиной y, расположенную на расстоянии r от оси трубы (рис.8.1).Площадь кольца ym = 2 нг yg. Расходы 148. Место, отношение d0,=, и расход потока Напомним замечания о независимости V от r, подставив значение (8.5) и значение (8.5、 Я = <8-7） О Или (2 =(8.8） 128U ^ ’ Важно отметить, что при заданном / расходе в трубе в условиях давления движение ламинарного потока пропорционально 4-му порядку диаметра.

Средняя скорость. Если Y =(2 / <<то уравнение средней скорости найдено g20sh(8.9） 32л> 8У если мы сравним формулу для Itach и V、 V = 0,5 itah, (8.U） То есть средняя скорость сечения напорного ламинарного потока в цилиндрической трубе круглого сечения равна половине максимальной скорости. Коэффициент кинетической энергии Локальный градиент скорости= g, т. е. изменениег. 2 Прямо пропорционально расстоянию r определенной точки (заданного слоя) от оси трубы. Градиент<0. 149. Касательное напряжение линейно возрастает от нуля на оси трубы до = на стенке (рис. 8.1). Один. Действительно, м = —а-р-р, Но м = ДГ гг 2У матчи п§ −1(7.31).

При турбулентном режиме течения закон распределения местных скоростей не может быть универсальным: с увеличением числа Рейнольдса, т.е. с уменьшением роли сил вязкости, распределение скоростей должно становиться все более равномерным. Людмила Фирмаль

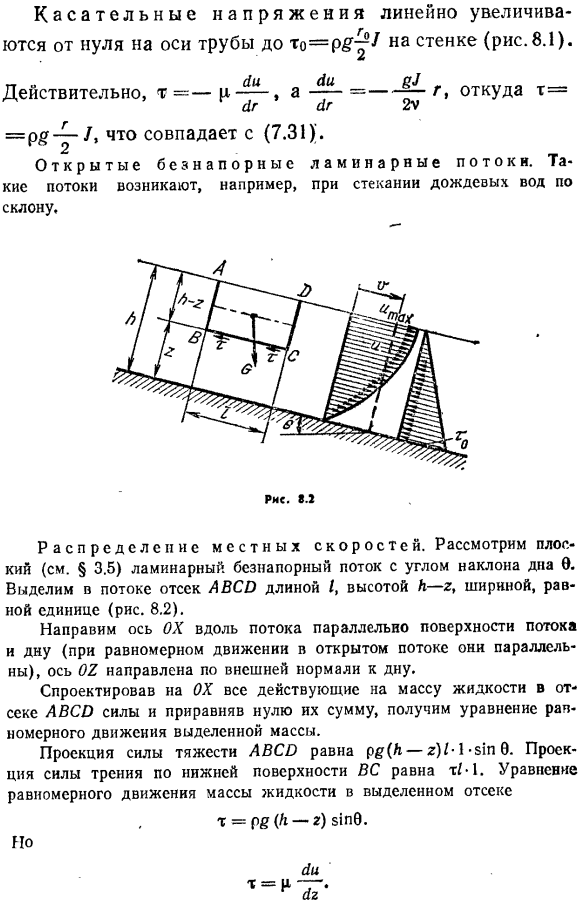
• Откройте ламинарный поток без давления. Такой поток возникает, например, когда дождевая вода идет вниз по склону. Локальное распределение скоростей. Рассмотрим плоское (см.§ 3.5) ламинарное свободное течение с углом наклона дна 0.In в проточном отсеке ABC выберите длину I, высоту A-2 и ширину, равную 1(рис.8.2). Ориентируйте ось OX вдоль потока параллельно поверхности и дну потока(если вы хотите равномерно перемещать его в открытом потоке, он параллелен). Если спроектировать все силы, действующие на массу жидкости в отсеке АВС с ОКС и сделать их сумму равной нулю, то получится уравнение равномерного движения выбранной массы.

Проекция силы тяжести ABCy равна p&(A-r) M $ m 0.Проекция силы трения на нижнюю поверхность самолета равна tM. Уравнение равномерного движения массы жидкости в выделенном отсеке Р =Р§(А-Р) 51n0. Но… Ли. 150. Назначьте предыдущее отношение и получите yi [Д. Для малого угла, Br0 = 1§ 0=», где r-наклон дна. И затем… (к-д) ый. Интегрирование в диапазоне от 0 до k дает n = ^ r(2A-r)+ C. для r = 0 константа интегрирования равна C = 0, поскольку скорость u = 0, а для распределения скорости открытого потока (8.11） Таким образом, скорость распределяется по глубине рассматриваемого потока вдоль параболы. Максимальная скорость в этом случае возникает на поверхности.

Смотрите также:

Курсовая работа по гидравлике

Возможно эти страницы вам будут полезны:

1. Средняя скорость и расход потока при равномерном движении жидкости.
2. Касательные напряжения и их распределение при равномерном движении.
3. Коэффициент Дарси при ламинарном напорном движении в трубе.
4. Линии тока и вихревые линии при ламинарном движении в круглой трубе.