Оглавление:
Расположение корней квадратного трёхчлена относительно одной-двух заданных точек («метод парабол»)
Многие задачи с параметрами сводятся к исследованию расположения корней квадратного трёхчлена относительно заданной точки или заданного промежутка (отрезка, интервала, луча). При этом если дискриминант D квадратного трёхчлена есть полный квадрат некоторого выражения (т.е. извлекается 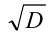 ), то в подавляющем большинстве случаев проще найти корни
), то в подавляющем большинстве случаев проще найти корни  ,
,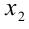 квадратного трёхчлена и подчинить их условиям задачи. Если же —
квадратного трёхчлена и подчинить их условиям задачи. Если же —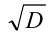 не извлекается (остаётся радикал), то в принципе также можно найти корни
не извлекается (остаётся радикал), то в принципе также можно найти корни  ,
,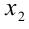 квадратного трёхчлена и подчинить их условиям задачи, но при этом придётся решать непростые иррациональные неравенства, которые приводят к большим и утомительным вычислениям. В этом случае более удобным оказывается следующий подход (иногда называемый методом парабол), использующий графическую интерпретацию расположения корней квадратного трёхчлена, вершины его графика по отношению к заданной точке (точкам).
квадратного трёхчлена и подчинить их условиям задачи, но при этом придётся решать непростые иррациональные неравенства, которые приводят к большим и утомительным вычислениям. В этом случае более удобным оказывается следующий подход (иногда называемый методом парабол), использующий графическую интерпретацию расположения корней квадратного трёхчлена, вершины его графика по отношению к заданной точке (точкам).
Итак, пусть задана квадратичная функция
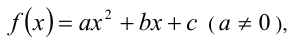
график которой имеет точки ,
,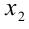 пересечения с осью абсцисс (т.е.
пересечения с осью абсцисс (т.е. 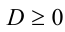 ). Пусть, для определённости, ветви параболы направлены вверх. Выпишем, например, условия, необходимые и достаточные для того, чтобы оба корня
). Пусть, для определённости, ветви параболы направлены вверх. Выпишем, например, условия, необходимые и достаточные для того, чтобы оба корня ,
, 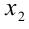 были меньше заданного действительного числа А . Очевидно, что в этом случае вершина параболы
были меньше заданного действительного числа А . Очевидно, что в этом случае вершина параболы 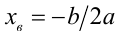 должна располагаться левее точки x = А , и значение данной квадратичной функции в точке А должно быть положительно. Таким образом, оба корня
должна располагаться левее точки x = А , и значение данной квадратичной функции в точке А должно быть положительно. Таким образом, оба корня  ,
,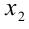 меньше заданного числа
меньше заданного числа 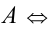
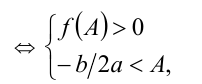
т.е. данная система условий однозначно задаёт рассматриваемую ситуацию в расположении корней по отношению к А .
Понятно, что по отношению к одному заданному числу А возможны всего три ситуации: оба корня меньше А , оба корня больше А , корни расположены по разные стороны от А . Если же заданы два действительных числа А и В , то по отношению к ним возможны уже четыре ситуации расположения корней квадратного трёхчлена. Оформим полученный специальный метод в виде следующей таблицы.
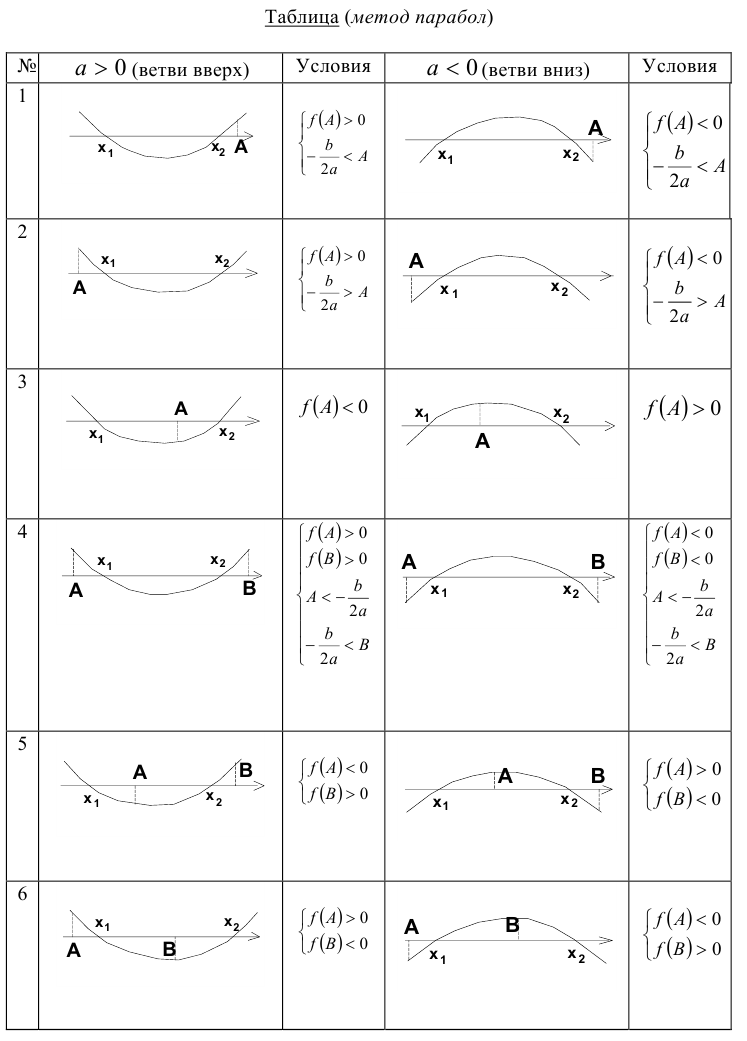
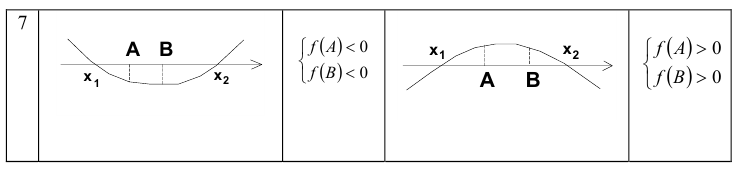
Замечание. При использовании данного метода внимательно читайте условие задачи. В зависимости от постановки задачи знак в неравенствах, приведённых в таблице, может быть как строгим, так и нестрогим. Неверно поставленный знак может привести к потере или, наоборот, к приобретению посторонних корней.
Пример №164.
Найти все значения параметра а , при которых корни уравнения 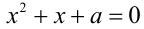 действительные, различные и оба больше а .
действительные, различные и оба больше а .
Решение:
В этой задаче реализуется случай 2 из таблицы выше. Обозначим 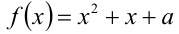 . В соответствии с методом, решение задачи сводится к системе
. В соответствии с методом, решение задачи сводится к системе
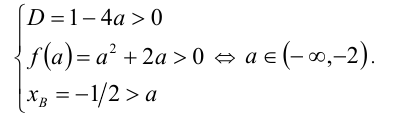
Пример №165.
При каких значениях 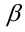 оба корня уравнения
оба корня уравнения 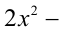
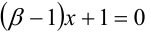 положительны и расположены по разные стороны от числа 3?
положительны и расположены по разные стороны от числа 3?
Решение:
Выпишем два способа решения задачи — стандартный и специальный, изложенный выше, и сравним их по эффективности.
Стандартный способ решения сводится к решению системы
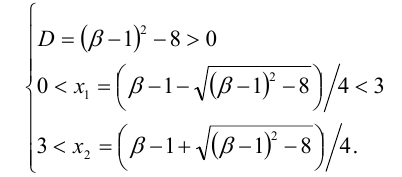
Специальный метод состоит в решении следующей системы (см. случай 6 в таблице; через f(x) обозначен многочлен в левой части уравнения):
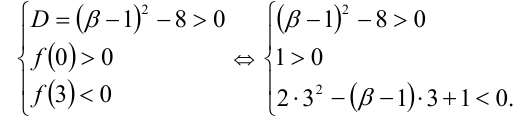
Условие положительности дискриминанта учтено в обоих способах решения. Но если при стандартном способе надо решать два иррациональных неравенства (одно из которых двойное), то при выборе второго способа вместо этого имеем два линейных неравенства (одно из которых тривиально). Безусловно, при решении данной задачи следует предпочесть второй вариант решения.
Ответ: 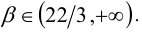
Пример №166.
Найти все значения параметра m , при которых один из корней квадратного трёхчлена
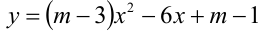
меньше, а другой больше двух.
Решение:
По условию 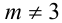 . В зависимости от знака старшего коэффициента
. В зависимости от знака старшего коэффициента 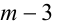 возможны два случая (см. пункт 3 в таблице):
возможны два случая (см. пункт 3 в таблице):
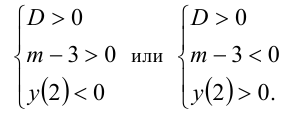
Заметим, что эти случаи легко объединить в один:
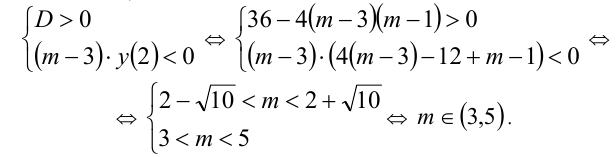
Пример №167.
Найти наибольшее значение параметра p , при котором функция
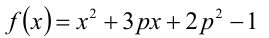
принимает отрицательные значения в интервале (0,1).
Решение:
По условию задачи составляем систему (см. пункт 7 в таблице):
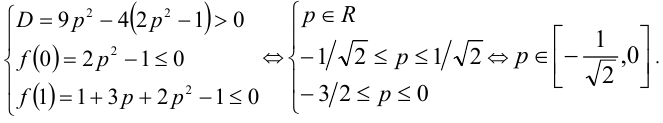
Ответ: наибольшее значение p равно 0.
Заметим, что необходимость использования приведённого метода при решении задач, связанных с корнями квадратного уравнения, возникает не всегда. Например, в следующей задаче вполне можно обойтись стандартным методом.
Пример №168.
При каких значениях параметра а больший корень уравнения
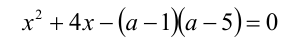
принадлежит промежутку [0,1) ?
Решение:
В данной задаче дискриминант является полным квадратом и, следовательно, корни имеют рациональные выражения: 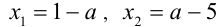 . Согласно условию задачи, возможны два случая.
. Согласно условию задачи, возможны два случая.
1) Если 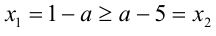 , т.е.
, т.е. 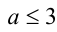 , то большим является корень
, то большим является корень 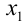 , и условие задачи приводит к неравенству
, и условие задачи приводит к неравенству 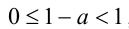 , откуда
, откуда 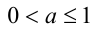 .
.
2) Если же 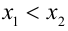 , т.е.
, т.е. 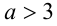 , то большим является корень
, то большим является корень 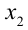 , и условие задачи приводит к неравенству
, и условие задачи приводит к неравенству 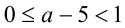 , откуда находим
, откуда находим 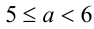 .
.
Ответ: 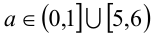 .
.
Общая рекомендация такова: если дискриминант квадратного уравнения является полным квадратом и, следовательно, корни имеют рациональный вид, во многих задачах приемлем (часто оказывается проще других методов) стандартный подход. Но если это не так и корни иррациональны, то более удобными могут оказаться специальный метод, эффективность которого была продемонстрирована выше на примерах, и теорема Виета, которые не требуют нахождения корней уравнения в явном виде.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

