Оглавление:
Раскрытие модуля, используя его геометрический смысл
Пусть 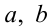 — действительные числа. Тогда выражение
— действительные числа. Тогда выражение 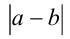 имеет геометрический смысл расстояния на числовой прямой от точки с координатой
имеет геометрический смысл расстояния на числовой прямой от точки с координатой 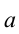 до точки с координатой
до точки с координатой 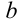 . Геометрическую интерпретацию модуля как расстояния бывает достаточно удобно использовать при решении некоторых уравнений и неравенств с модулями.
. Геометрическую интерпретацию модуля как расстояния бывает достаточно удобно использовать при решении некоторых уравнений и неравенств с модулями.
Например, решить уравнение 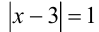 геометрически означает найти на числовой прямой все точки
геометрически означает найти на числовой прямой все точки 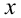 , расположенные от точки 3 на расстоянии 1. Представим себе числовую прямую, отметим на ней точку, отвечающую числу 3, и отложим в обе стороны от неё единичные отрезки. Получим две точки, координаты которых
, расположенные от точки 3 на расстоянии 1. Представим себе числовую прямую, отметим на ней точку, отвечающую числу 3, и отложим в обе стороны от неё единичные отрезки. Получим две точки, координаты которых 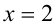 и
и 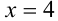 будут искомыми решениями уравнения.
будут искомыми решениями уравнения.
Другой пример. Пусть требуется решить неравенство 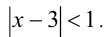 Это означает, что надо найти на числовой прямой все точки, отстоящие от точки 3 на расстояние, меньшее 1. Опять представим себе числовую прямую, отметим на ней точку 3, отложим от неё в обе стороны отрезки единичной длины и получим две точки 2 и 4 (их следует выколоть). Тогда искомые точки
Это означает, что надо найти на числовой прямой все точки, отстоящие от точки 3 на расстояние, меньшее 1. Опять представим себе числовую прямую, отметим на ней точку 3, отложим от неё в обе стороны отрезки единичной длины и получим две точки 2 и 4 (их следует выколоть). Тогда искомые точки 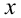 образуют интервал с центром в точке 3 длины 2, т.е.
образуют интервал с центром в точке 3 длины 2, т.е. 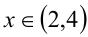 . Таким же образом можно решить неравенства
. Таким же образом можно решить неравенства 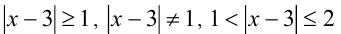 и многие другие.
и многие другие.
Рассмотрим теперь более сложный пример.
Пример №273.
Решить неравенство
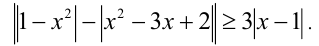
Решение:
Так как 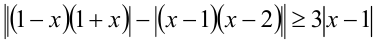 , то перенесём все слагаемые в левую часть и разложим её на множители
, то перенесём все слагаемые в левую часть и разложим её на множители
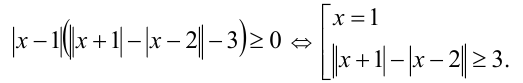
Решим последнее неравенство, привлекая геометрический смысл модуля. Представим числовую прямую и на ней точки — 1 и 2 .

Решить неравенство 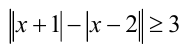 означает найти на числовой прямой такие точки
означает найти на числовой прямой такие точки 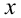 , что модуль разности расстояний от
, что модуль разности расстояний от 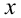 до точек — 1 и 2 не меньше 3 . Заметим, что расстояние между этими точками в точности равно 3 . Если точка
до точек — 1 и 2 не меньше 3 . Заметим, что расстояние между этими точками в точности равно 3 . Если точка 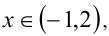 то сумма расстояний от неё до — 1 и 2 равна 3 , а соответствующая разность расстояний будет меньше 3, т.е. неравенство не выполняется. Если же
то сумма расстояний от неё до — 1 и 2 равна 3 , а соответствующая разность расстояний будет меньше 3, т.е. неравенство не выполняется. Если же 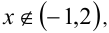 то модуль разности расстояний от
то модуль разности расстояний от 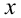 до — 1 и 2 будет равен 3, т.е. неравенство верно. Таким образом, получаем ответ:
до — 1 и 2 будет равен 3, т.е. неравенство верно. Таким образом, получаем ответ: 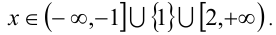
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

