Оглавление:
Раскрытие модулей но определению
Если в задаче содержится модуль (как правило, один), то рассматривают два случая: когда выражение под знаком модуля больше либо равно нулю и когда оно меньше нуля. В первом случае модуль опускают (это часто называют «раскрыть модуль со знаком плюс»), а во втором — модуль заменяют скобками, перед которыми ставится знак минус (называется «раскрыть модуль со знаком минус»), В отдельных задачах бывает удобнее рассмотреть три случая: когда подмодульное выражение больше, меньше или равно нулю. Например, уравнения вида 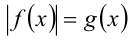 этим способом сводятся к совокупности двух систем
этим способом сводятся к совокупности двух систем
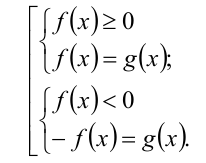
Аналогично можно решать неравенства вида 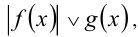 где знак
где знак  заменяет любой из знаков неравенства.
заменяет любой из знаков неравенства.
Замечание. Раскрывать модули по определению можно и в случаях, когда их количество в задаче больше одного, но тогда, например, при решении уравнения 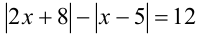 придётся рассмотреть четыре случая:
придётся рассмотреть четыре случая:
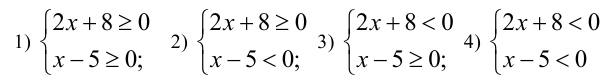
(и в каждом случае раскрывать модули и решать уравнение), в то время как при использовании метода интервалов — всего три:
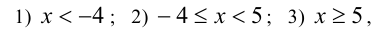 что эффективнее. Рас-смотрим соответствующие примеры.
что эффективнее. Рас-смотрим соответствующие примеры.
Пример №257.
Решить уравнение 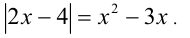
Решение:
Рассмотрим два случая:
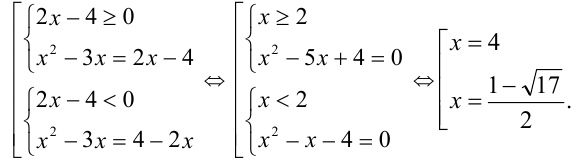
Пример №258.
Решить неравенство
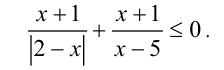
Решение:
Раскладывая левую часть неравенства на множители, имеем
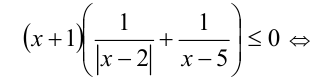
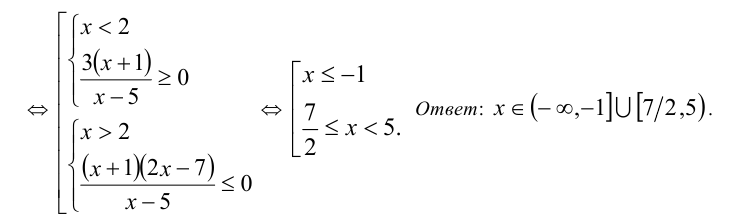
Пример №259.
Решить уравнение
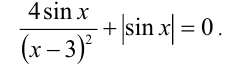
Решение:
ОДЗ: 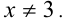 Рассмотрим два случая:
Рассмотрим два случая:
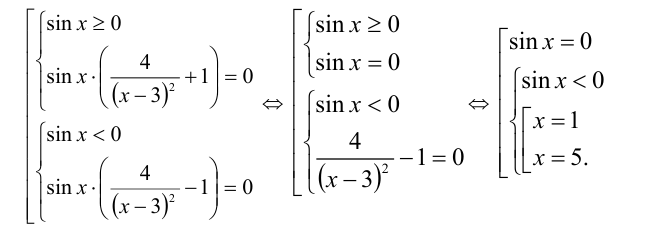
Ответ: 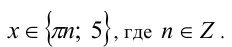
Пример №260.
Решить уравнение 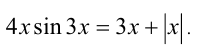
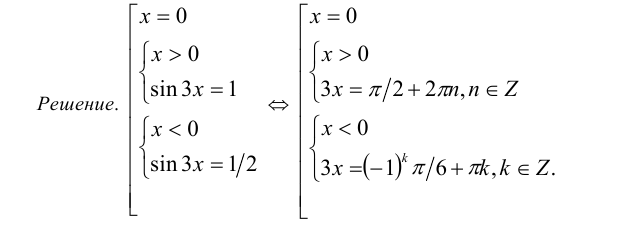
Ответ:
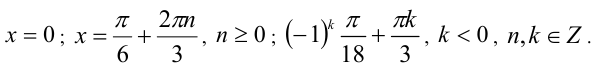
Пример №261.
Найти все пары (х;у), удовлетворяющие условию 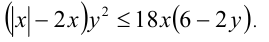
Решение:
1) При x = 0 неравенство верно при любом действительном у. Отсюда получаем пары чисел где 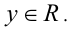
2) При x >0 имеем: 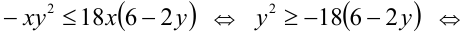
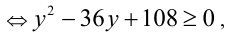 откуда получаем пары чисел вида
откуда получаем пары чисел вида 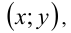 где
где 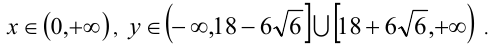
3) При 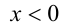 имеем:
имеем: 
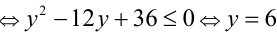 т.е. получили пары
т.е. получили пары 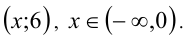
Ответ: 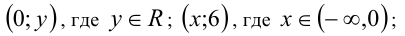
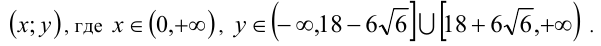
Пример №262.
Решить неравенство 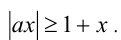
Решение:
Здесь целесообразно вначале «отделить» параметр от переменной 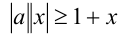 , и уже затем раскрывать модуль, но только над x .
, и уже затем раскрывать модуль, но только над x .
1) При 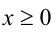 имеем:
имеем: 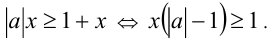
Если 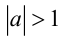 , то решением будет
, то решением будет 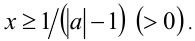 Пересекая с промежутком
Пересекая с промежутком 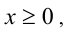 получаем
получаем 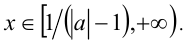 Если
Если 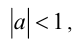 то решением будет
то решением будет 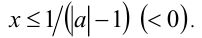 Пересекая с промежутком
Пересекая с промежутком 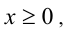 получаем
получаем 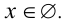 Если
Если 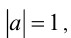 то неравенство примет вид
то неравенство примет вид 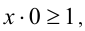 что не выполняется ни при каких x .
что не выполняется ни при каких x .
2) При 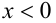 имеем:
имеем:
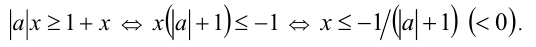
Пересекая с промежутком 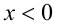 получаем, что при всех а реше-нием будет любое
получаем, что при всех а реше-нием будет любое 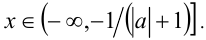 Осталось объединить полученные решения.
Осталось объединить полученные решения.
Ответ: при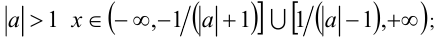 при
при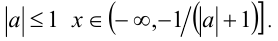
Пример №263.
Найти сумму целых решений неравенства
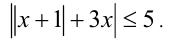
Решение:
В этой задаче имеются вложенные модули. Раскроем их, начиная с внутреннего модуля. Для этого рассмотрим два случая.
1)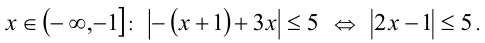 Посколь-ку на рассматриваемом промежутке
Посколь-ку на рассматриваемом промежутке 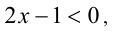 то оставшийся модуль раскрывается со знаком «минус», и получаем
то оставшийся модуль раскрывается со знаком «минус», и получаем 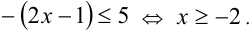 Пересекая с данным промежутком, имеем результат:
Пересекая с данным промежутком, имеем результат: 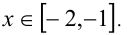
2) 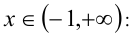 раскрывая внутренний модуль, получаем
раскрывая внутренний модуль, получаем 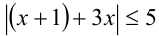
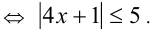 . Если при этом
. Если при этом 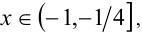 то имеем
то имеем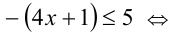
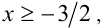 пересекая с данным промежутком, получаем решения
пересекая с данным промежутком, получаем решения 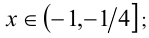 если же
если же 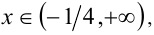 то имеем
то имеем 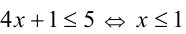 или, с учётом промежутка,
или, с учётом промежутка, 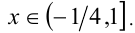 Объединяя результаты, находим множество всех решений неравенства:
Объединяя результаты, находим множество всех решений неравенства: 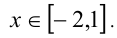
Ответ: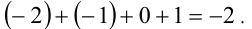
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

