Оглавление:





Расчёт статически неопределимых систем по способу допускаемых нагрузок
- Расчет статически неопределенной системы методом допустимой нагрузки. Применяя метод допустимого нагружения к статически неопределенной системе, стержень изготавливают из материала, который может понести значительные потери, например из стали.
Как одна из трех кривых силы Q (рис. 57). Сделайте все полюсы сделаны из низкоуглеродистой стали с прочностью выхода. Длина крайнего стержня, как упоминалось выше, указывает на длину zi, среднего Z3. Допустимое напряжение[o]=. Как Пластическая деформация нагруженных стержней из низкоуглеродистой
стали- А предварительно, при расчете этой статически неопределенной Людмила Фирмаль
системы, дают отношение площади стержня. Затем решите проблему, как указано в§ 19:、: Н J г 3 1+2COS8a’ Вопрос COS8a л+2С о С8<х * Потому что средний род-это супер-подчеркнула; следовательно, крест-секционный вариант площадь F должен быть сделан по формуле = _ — П0±2ПК^adzg 4Н. м., Беляев, расчет допустимой нагрузки[гл. В Необходимо придать боковым стержням такое же количество площади. Метод допустимого нагружения
применим; состояние прочности: Что в данном случае следует понимать под конечной нагрузкой конструкции? Поскольку конструкция выполнена из материала с пределом текучести, назовем эту нагрузку QJ, что соответствует достижению состояния текучести для всей конструкции, а также простому растяжению стержня из такого материала. Дальнейшая деформация (точка опускания а) требует увеличения нагрузки,
пока сила Q не достигнет этого значения. Когда Q становится равным Q, дальнейший рост деформации уже происходит без увеличения нагрузки, и конструкция выходит из строя. Чтобы определить значение Q, рассмотрим постепенный ход трансформации нашей барной системы. Поскольку средний полюс более напряжен, чем крайний, напряжение достигнет предела текучести, который раньше, чем другие. Он будет равен QT=(1-| — 2cos3a) N1.N l=Far-усилие промежуточного стержня, соответствующее его пределу текучести. Напряжение крайних
стержней с одинаковой площадью в это время еще не достигло предела текучести, и эти стержни упруго сопротивляются дальнейшей деформации. Для того, чтобы эта деформация произошла, напряжение крайнего стержня также должно увеличить нагрузку дальше, пока она не достигнет предела текучести. В нагрузке QT напряжение промежуточного стержня уже достигло предела текучести, поэтому при достижении максимальной грузоподъемности конструкции нагрузка будет еще больше увеличиваться,
и без увеличения силы левая наша статически неприводимая система состоит из превращения в статически определяемую систему. в — Людмила Фирмаль
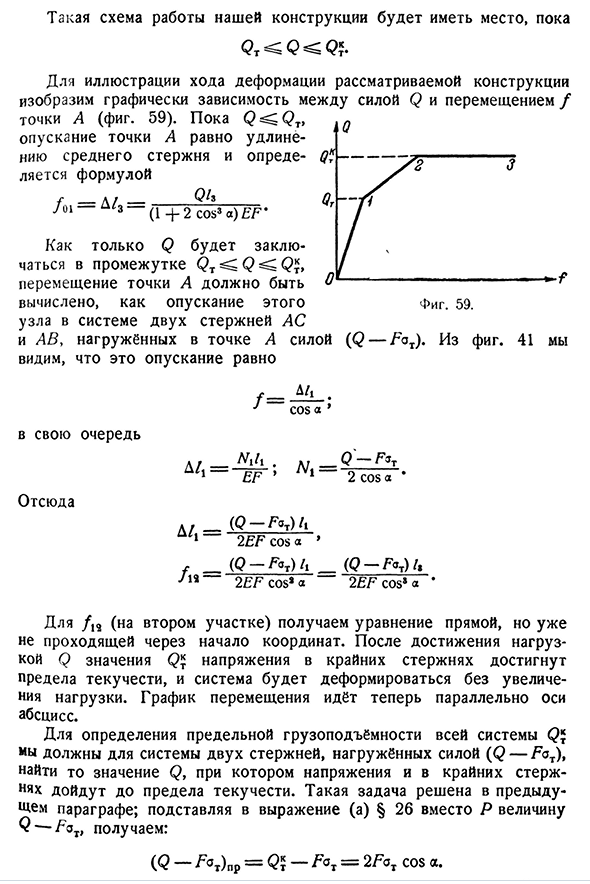
Из двух стержней AB и AC AFJ, нагруженный нисходящей силой Q и известной силой в точке A, равен fat(рис. 58).§ 27] расчет метода допустимой нагрузки 99 Эта схема нашей проектной работы является、 Графически изобразим зависимость между силой Q и смещением f точки A для объяснения процесса деформации возможной конструкции (рис. 59). А Q^Q и Т, капли в точке А равна удлинение среднего полюса и определяется по формуле УФ-д/-Которна Qt、 Ноль один — ^з—(1+2С о С3А)е Ф. Когда Q находится в интервале, QR Q q * T движущаяся точка A является# ———————— ~ • эта цифра была рассчитана путем опущения. Узел в системе из двух стержней AC и AB нагружен точечной силой (Q-fat), которая равна 59. О фигуре. 41 мы видим
, что это снижение равноценно В порядке М. Кос-а А / —(Г-^Т)Зи 1-2£Ф потому что’ / _ (М-ф°А11(г жира) Зет8 713~2EFcos * a-2EF cos8a • И так оно и есть. В /12 (следующий раздел) мы получаем уравнение линии, но она больше не проходит через начало координат. После того как нагрузка q достигает значения Q, напряжение крайнего стержня достигает предела текучести и система деформируется без увеличения нагрузки. График смещения параллелен горизонтальной оси. Чтобы определить максимальную грузоподъемность всей системы Q, нам нужно найти значение для системы из двух стержней, нагруженных силой (Q-FaT). Подставляя P-значение Q-fa T вместо выражения (a)§ 26, Вы получаете: (М-ф т) НП= — жир = 2faT потому что. 4 * 100 расчет допустимой нагрузки (гл. В И так оно и есть. БС=Ф Т(1 4 ″ 2cos а). Допустимая нагрузка будет равна следующим значениям п Qt_FaT(1+2cosa) H’Pop-k-k И если мы скажем — ^ — =
[a]、 Вопрос * о=р [°] (1+2cos а). Наконец:а* Обычным способом получаем: Q=4t, a=30°, [ac]=1000кг] см*(сталь). И Гр— _____4_0_0_0 __ — 1. 7 ″ 4L GM * * 9~1000 (1+2cos3 30°)’ По методу допустимой нагрузки FS4000, l9-1000(1+2cos30°) — 1, 4 6cm • Поэтому понятно, что мы проектируем статически неопределенную систему материалов с пределом текучести экономичнее, чем при расчете допустимого напряжения методом расчета допустимой нагрузки: в методе расчета допустимого напряжения максимальной нагрузкой нашей конструкции считается величина ft, где только материалоемкость промежуточного стержня достигает предела текучести. материал всех трех стержней полностью используется. Таким образом, новый метод расчета основан на статически неопределенной системе достижения увеличения их расчетной несущей способности и фактической
прочности всех частей конструкции. Нетрудно расширить этот метод, если соотношение площадей промежуточных и крайних стержней не равно.§ 28] применение метода допустимой нагрузки 101 Приведенные выше теоретические соображения неоднократно проверялись опытом, и всегда существует достаточно тесная сходимость значений расчетных критических нагрузок, которая определяется экспериментом. Это дает уверенность в правильности теоретических предположений метода допустимых нагрузок.
Смотрите также:

