Расчёт бесконечно длинной балки на упругом основании, загружённой одной силой Р.

Расчёт бесконечно длинной балки на упругом основании, загружённой одной силой Р.

• Расчет бесконечно длинной балки на упругом основании, нагруженном одной силой p. Решение этой задачи позволяет рассчитать луч конечной длины с помощью последовательных приближений. Начало координат находится в точке приложения

силы Р. Так как вся реакция основания, равная силе Р, должна иметь конечное значение, то отклонение луча в точке, бесконечно удаленной от точки приложения силы, должно исчезнуть.: =0.

Решена задача о бесконечно длинных балках, один фокус которых изгибается(рис. 403). Помимо научно-практических (25.5) X CO При Людмила Фирмаль

бесконечно больших значениях X второй член (25.4)правой части выражения исчезает для множителя. Таким образом, A=0 и B=0; г=е~$х (грех РХ+Д, потому что РХ). (25.6) кроме того, в зависимости от симметрии нагрузки и реакции основания, касательная к кривой оси в точке приложения силы должна быть параллельна абсциссе: дуплексный Дифференцируя (25.6), получаем: =6= — [sin px(C+D) 4-cos (D-C)]. Подставляя эту формулу x=0 и уравнивая результат до нуля,

вы увидите, что D-C=0 и C=D-t Уравнение выглядит так: y=e — $x C (sin px+cos), (25.7)=O=—C≡sin (25.8) для определения последней константы C существует другая формула. Если отрезать участок балки в точке О справа от силы Р и рассмотреть правую часть балки, то боковая сила этого участка равна реакции основания, действующей на правую половину балки XXVUNIT описание В

• списках. Так как реакция направлена вверх (в правую половину) и вся реакция основания равна P, то боковая сила в поперечном сечении l*=0 равна М (Л)Х- = О П Два. * Но с другой стороны, И так оно и есть., Рассчитано с использованием (25.8), Д * Г dx2 =Вопрос (*)• ЭДЖ Д * Г Д Х9 = — 2Cfi2e~^x[COS fix-sin px],=4-4Cfise v COS fix. уб Если вы назначаете (25.12) на (25.10) и выравниваете x до нуля、: 4EJCp3= — Y и C=Р 8Э/Р5′ Значение Y и его производная имеет вид Г= — е 7 классы(В+С О s1U)= » в W7″ запрос=9-+4EJP Е С в=+4EJP8 ’г3′

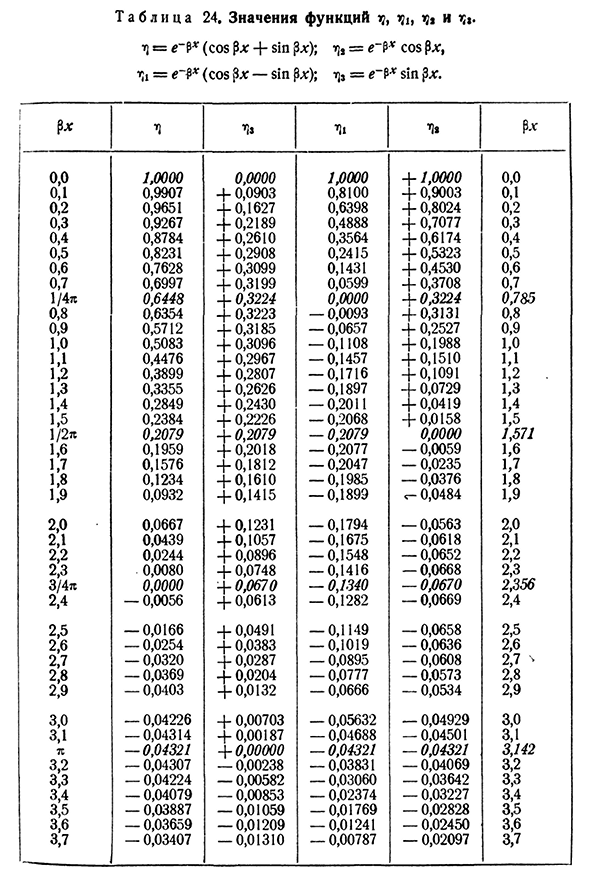
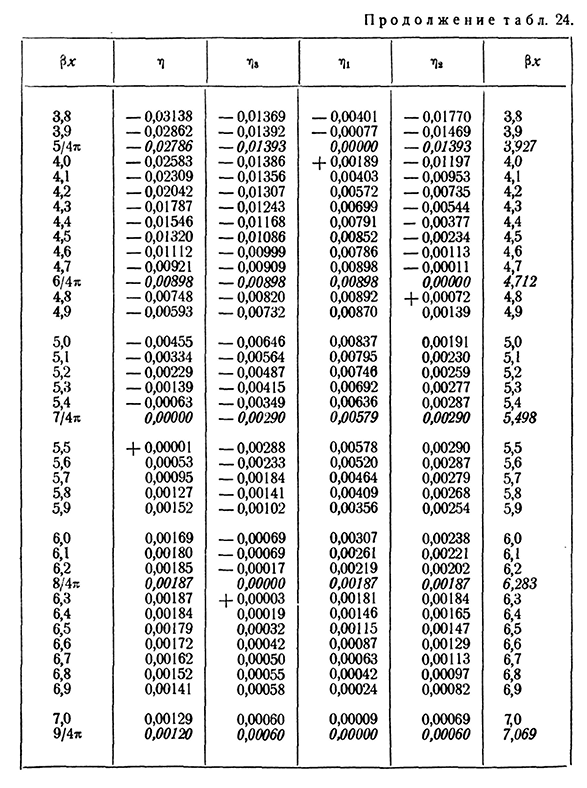
м(х)=Эдж== + ~у,₽[потому что$X-грех∙х]=%Г (Х) = е^=—е-? Икс Кос? х — = — г•я) С. (25.9) (25.10) (25.11) (25.12) (25.13) (25.14) (25.15)) (25.16)) (25.17) д.± Д х Z’ Таким образом, напряженное состояние и деформация балки на упругом основании полностью определяются нагрузкой и коэффициентом Р, зависящим от отношения жесткости балки к упругому основанию. Значения аргументных функций px [t], TC, t]2, t и z приведены в таблице 24. Значение коэффициента k 

изменяется очень сильно в зависимости от вида причины; назовем ширину Людмила Фирмаль

луча B, k=k^B можно представить этот коэффициент как, где так называемый. Диапазон почв средней плотности составляет от 0,5 до 5 кг!5 см плотного грунта от 10 кг/см\3}для кладки, в качестве основания под балки, от 400 до 600 кг! для сми 800-1500 кг бетона! поскольку формула cm * P содержит k, даже значительные вариации величины ki относительно слабо отражаются на результатах расчета.§ 153] расчет балки бесконечной длины на упругом основании 477 Значения Т А Б Л и Ц А24 Ф елей и тп. т) = е -?х (Кос+Син ПВ); Т)2= = е~х$, потому что ТК=Е~#Х (потому что исправить-исправить грех)}tj3=е~$х Sin в интернет

Смотрите также:

• Примеры решения задач по сопромату

Расчёт трёхпро­лётной балки	Расчёты балок конечной длины
Балка на упругом основании. Общие понятия.	Косой изгиб. Основные понятия