Оглавление:



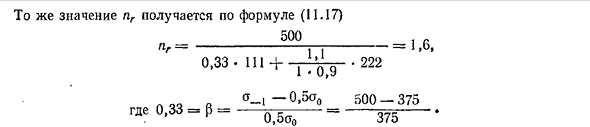

Расчеты на прочность при переменных напряжениях
- Расчет прочности при переменном напряжении Прочность при переменном напряжении оценивается фактическим значением коэффициента безопасности n путем сравнения его с допуском [u].
Формат условия прочности следующий. n> [u]. (1114) Коэффициент безопасности можно приблизительно определить, используя, например, принципиальную схему предельного напряжения, как показано на рисунке 5. 11,7.
Во-первых, коэффициент безопасности Людмила Фирмаль
лабораторного образца определяется как d0 = от 6 до ~ 12 мм в предположении, что рабочий цикл, для которого определяется коэффициент безопасности, совпадает с соответствующим предельным циклом, даже если нагрузка изменяется Будет. Угол А определяется по известным значениям амплитуды и среднего
напряжения. тг «= — ^. (11.15) Луч 0 — I рисуется под углом a от начала координат диаграммы (см. Рис. 11.7). Текущая точка M (tsa; from) на линии характеризует рабочий цикл, а точка N (poa; pat) является предельным значением для того же цикла. Коэффициент безопасности равен соотношению сегментов. • Если точка N
- находится внутри линии AB, усталостное разрушение произойдет, если напряжение цикла возрастет. В этом случае (11.5a) принимает вид o_ 1-4-IDT, Коэффициенты безопасности, связанные с усталостным разрушением (для лабораторных образцов), равны ° -1 стр —- (11.16) + Чтобы получить реальный коэффициент безопасности детали, необходимо учитывать влияние концентрации напряжений, масштабного коэффициента и качества обработки поверхности. В реальных расчетах поправочный коэффициент относится только к
переменной части цикла напряжения, то есть амплитуда цикла J (11.20) (11 21) Пример. Определить коэффициент усталостной безопасности для поршневых трубчатых штифтов, нагруженных силой P, в диапазоне от Pmax = 60 кН (6000 кгс) до Pmin = –20 кН (-2000 кгс) (рис. 11.18, а). а = 30, б = 50, 9 2-256 241D = 30, D = 16 мм. Механические свойства материала пальца: = 800 МПа (8000 кгс / см2), (График М показан на рисунке 11.18, б). Момент перетаскивания раздела Максимальный и минимальный изгибающие моменты и соответствующие нормальные напряжения: L4.ax = 1,375Rm ax = 1,375 • IO «2 • 60000 = 825 Нм (8250 кгс.см); максимальная Mmax 825 •
106 2,48 333 МПа (3330 кг / см2); W L! Миссия = 1 375 • IO «2 Rmin = 1375 • IO ‘2 (-20 000) = -275 Нм (-2750 кгс • см); М минут Минимум 275 дюймов 10e Людмила Фирмаль
2,48 = -111 МПа (-1110 кгс / см2). G Амплитуда рабочего цикла и среднее напряжение: MIX MIN 333 “” (111) ОСО ЛХГГ / ОООЛ т <ta = ——— g ——— = ———— ——— = 222 МПа (2220 кгс / см2) ); ° max + ° min 3 3 3- | — (- 111) ,, J irT от = ——— = 111 МПа (1110 кгс / см2) Рассчитать амплитуду цикла пульсации и средние пределы напряжений а ‘а0 = атс = -Г = «Г- = 3 7 5МПа (3 7 5 0 кгс / см2). Создайте диаграмму предельного напряжения на основе известных значений o_ |, oa и from (рис. 11.18, c). Исходя из координатной точки диаграммы, нарисуйте луч O-N под углом a,
определяемым уравнением oa k 222 g a-o ^ adG-111 4br «2n». «68» — я думаю, что рабочий цикл и предельный цикл схожи: координаты точки M и напряжения рабочего цикла: Od = Oa —6— = 272 МПа (2720 кгс / см2); st = 111 МПа ( 1110 кгс / см2) P Тот же цикл с точкой N gsa = 435 МПа (4350 кгс / см2) и fr = 178,5 МПа (1785 кгс / см2) с координатой предельного напряжения n находится на одной линии ВКЛ. Коэффициент безопасности определяется как доля амплитуды, взятая в соответствии с графиком, Такое же значение 242 пг получается уравнением (11.17) 500. — J j 0,33-111 + -p- ’(fg … 222 1,6, Где 0,33 = P = o (-O, 5o0
Смотрите также:
| Линейное напряженное состояние | Долговечность |
| Плоское напряженное состояние | Длительная прочность при переменных нагрузках |

