Оглавление:




Расчет внецентренно сжатой гибкой стойки
- Расчет смещенной от центра гибкости сжатия Стеллаж Большой реализацией является задача сжатия сердечника гибкого стержня, работающего в пределах интересующей упругой деформации. Эта задача особенно интересна тем, что она представляет собой сложную нелинейную зависимость между напряжением и силами сжатия.
Благодаря этому ВОП- 474 рос о прочности таких стержней отнесены к особому классу задач, существенно отличающихся от ранее изученных. Для риса. 400 показывает сжатую стойку,
которая отклоняется от центра. Если стойка достаточно гибкая, то нельзя Людмила Фирмаль
игнорировать деформацию стойки при определении изгибающего момента. Изгибающий момент любого сечения определяется равенством M=P (B+e-V).e-эксцентриситет силы P. V-горизонтальное отклонение любой точки оси стержня. Дифференциальное уравнение для изгиба принимает вид Или Е / г Куда? В отличие от центральной задачи сжатия, получены неоднородные уравнения. Интеграл этого
уравнения состоит из двух членов. Первый-это решение однородного уравнения, второе-частичное решение с учетом правой части. При выполнении интеграции вы получаете V-A-KX4-Vz1p KX+o+2. (15.11) используйте граничные условия для определения интегральных констант A и B. угол поворота уплотнения равен нулю, справа =[- А to81p х+V, чтобы Соз х}ч=г=В * К=0,ч=0, следовательно, в=0. Движение
- в уплотнении также равно нулю:=L — / — o — / — e=0, Откуда Л=-(8+е). Подставляя значение A в уравнение (15.11), получаем V=(8+e) (1-Soz). (15.12) ‘<1U1s1x я Извлечение из выражения 475 (15.12)значение равно 8. Когда x-1V=8, так (8+е)(1-поп К1)-8. Эта формула более удобна для решения относительно значений(о-е). Для этого добавьте значение e в правую часть и вычтите то же самое значение. Это решение является 8+е=_1_. Попс С Присвоив это значение выражению (15.12) В- — — — (1
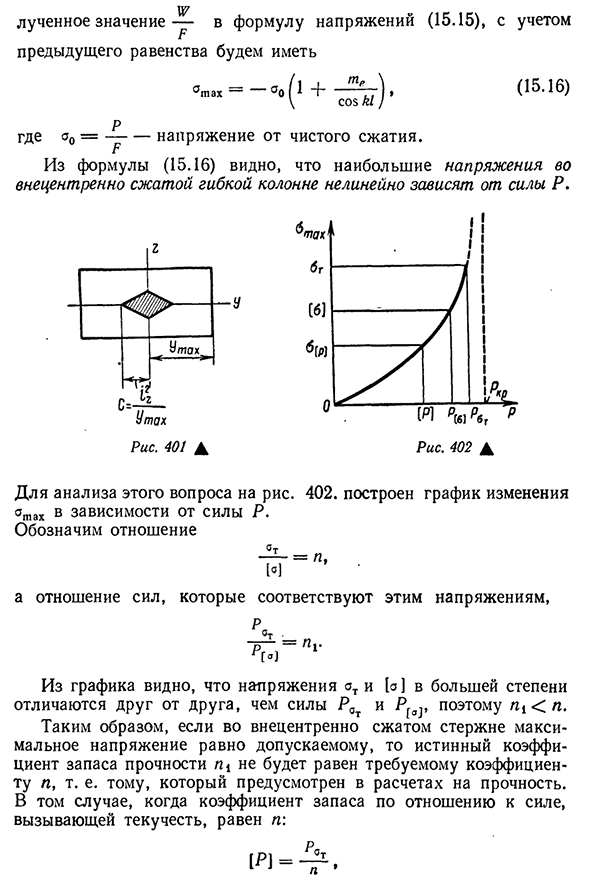
изгибающий момент уплотнения: М^=р(б+е)~ -^. (15.14) Попс С Наибольшее сжимающее напряжение уплотнения при сжатии и изгибе равна Т’ ° (15.15)) Узнайте ниже Г п ут П ут Из Формулы (11.15) видно, что Единое время Величина C представляет собой расстояние от центроида до полюса основной части (рис. 401). Через них показано отношение эксцентриситета к расстоянию до полюса секции сердечника И назовем это относительной эксцентричностью. Заменять- 476 измеренных величин-с учетом, в Формуле напряжения (15.15) Е Предыдущее уравнение-tah—°o(1 4—— ТТ)>(15.16) \ Соз С / п
Где A0 — — — — — — — напряжение от чистого сжатия. П Из этого уравнения(15.16) видно, что максимальное напряжение гибкой колонны, сжимаемой Людмила Фирмаль
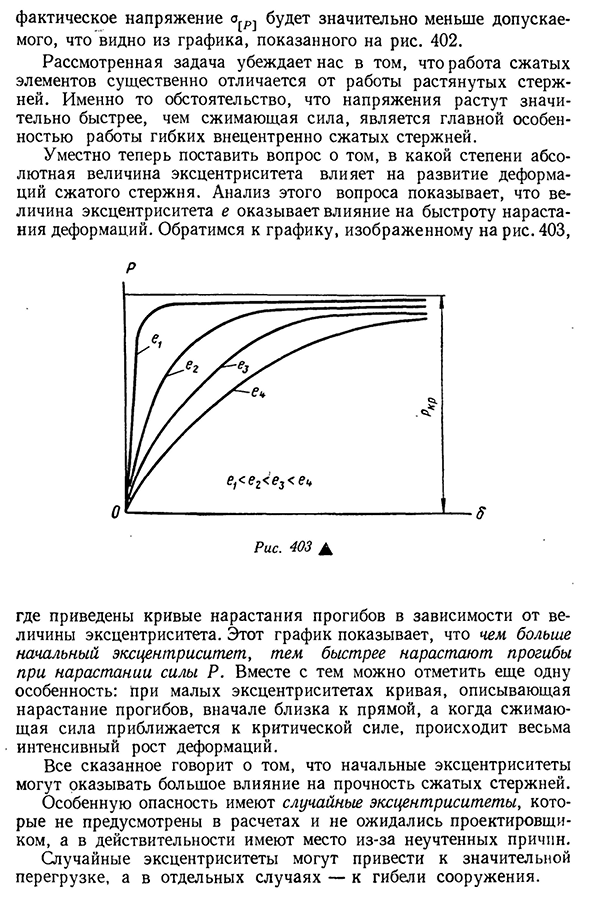
из центра, нелинейно зависит от силы P., 401a часы рис См. диаграмму для анализа этого вопроса. Мы построили график изменения АТАКСА в зависимости от 402 P-силы. Показать взаимосвязь ул —— =Р, [О]] Соотношение сил, соответствующих этим напряжениям, График показывает, что напряжения AT и[o]отличаются друг от друга, чем силы PCT и P[a], поэтому p1<^p. Таким образом, если максимальное напряжение внецентрового сжатого стержня равно допустимому напряжению, то истинный запас прочности Р^обеспечивается необходимым коэффициентом р, то есть прочностным расчетом. Если коэффициент запаса, связанный с силой, вызывающей ликвидность, равен n: 477 фактическое напряжение а(.p]намного меньше, чем допуск, как вы можете видеть из приведенного графика. 402. Рассмотренная задача убеждает нас в том, что работа сжатого
элемента существенно отличается от работы растянутого стержня. Дело в том, что давление растет гораздо быстрее, чем сила сжатия, что является основной особенностью работы сердечника сжатого стержня в гибком состоянии. Уместно поставить вопрос о том, насколько абсолютное значение эксцентриситета влияет на развитие деформации сжатого стержня. Анализ этого вопроса показывает, что величина эксцентриситета Е влияет на скорость нарастания деформации. Давайте посмотрим на показанный график. Четыреста три, Рис 403± Где находится кривая увеличения прогиба в соответствии с эксцентриситетом? Этот график показывает, что чем больше начальный эксцентриситет, тем быстрее прогиб увеличивается с увеличением силы R. Это говорит о том, что
начальный эксцентриситет оказывает существенное влияние на прочность сжатого стержня. Существует особая опасность случайного эксцентриситета, который не был предусмотрен в расчетах и не ожидался конструктором, но на самом деле он возникает по неизвестной причине. Случайный эксцентриситет может привести к серьезным перегрузкам, а в некоторых случаях и к гибели конструкции.
Смотрите также:

