Оглавление:


Расчет винтовых пружин
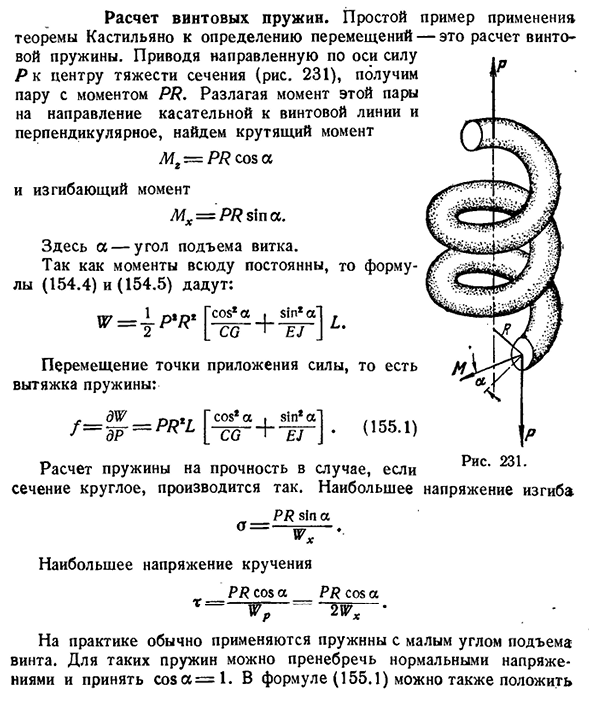
- Расчет винтовых пружин. Простым примером применения теоремы Кастильяно к определению смещения является расчет винтовых
пружин. Сила Р направлена вдоль оси к центроиду сечения (рис. 231), мы получаем в паре с моментом PR.
Если разложить моменты этой Людмила Фирмаль
пары в направлении, касательном к спирали и перпендикулярном, то крутящий момент Af*=P/?коза. И когда он поворачивается МХ =
пиар-грех. Где а-угол подъема катушки. Поскольку момент везде постоянен, формулы (154.4) и (154.5) будут иметь вид: Перемещение точки действия силы, то есть извлечение пружины: Расчет прочности пружины в случае круглого сечения осуществляется следующим
- образом. Максимальное напряжение на изгиб Пиар и грех Максимальное напряжение кручения Потому что пиар пиаром, потому что a2iFx • На практике обычно используются пружины
с небольшим углом подъема винта. В случае таких пружин можно пренебречь обычным напряжением и принять c o s a=L.
В формулу (155.1) можно также поставить общую теорему о сопротивлении Людмила Фирмаль
материала[глава XIV а=0. Возьми: И 7CG Допустимое напряжение [t] пружины может быть принято очень большим, учитывая высокие механические свойства используемого провода.
Смотрите также:
| Теорема о взаимности работ | Теорема о минимуме энергии |
| Теорема Кастильяно для линейных упругих систем | Интеграл перемещении |

