Оглавление:





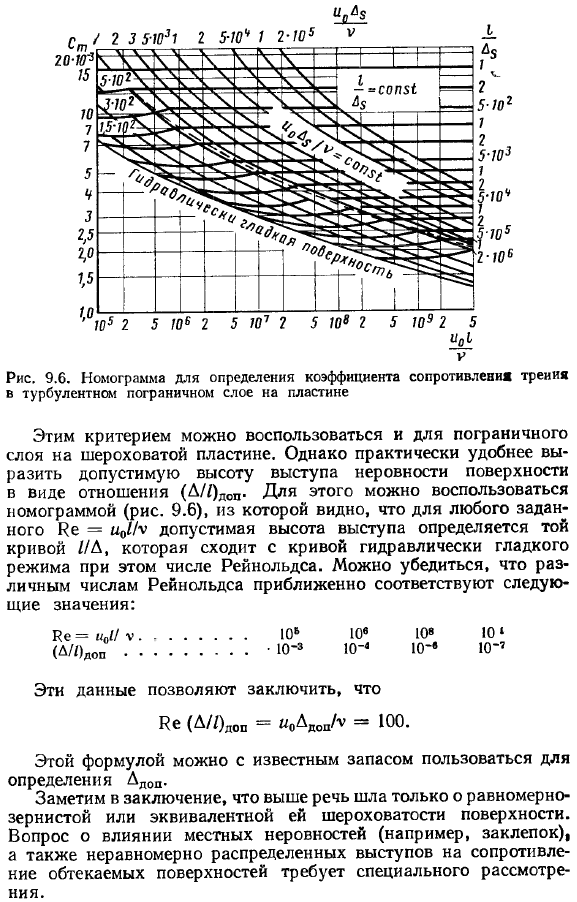

Расчет турбулентного пограничного слоя на пластине
Расчет турбулентного пограничного слоя на пластине. Предположим, что она сформирована по всей длине, начиная от передней кромки, на гладкой пластине с длиной / турбулентной границей layer. In другими словами, ламинарное сечение пограничного слоя вблизи переднего конца пластины считается незначительным. В этом случае для внешнего потока существует условие V =и 0-sop $ 1 n V = 0.Таким образом, уравнение импульса принимает вид: (9.4) _ т0 ДХ Ри * Если предположить, что пограничный турбулентный слой начинается на переднем конце пластины, то заметим, что формула для определения сопротивления трению (8.85) остается верной для разности, но величина 6 G *определяется соотношением турбулентного слоя, показанным ниже. Выражение (9.4) содержит 2 неизвестные функции. б * * (х) и М0(х).
Например, на основе эксперимента мы можем получить недостающее уравнение, установив зависимость между касательным напряжением m0 и толщиной потери импульса. Людмила Фирмаль
- Это отношение обычно называют законом сопротивления. На основе многих 368 WOBB* * \ » / в ИГ = 0-00655(«-) (9.5) Численный эксперимент, выполненный с большим числом Рейнольдса (Ke = u01/\), дает степенную зависимость Какое выражение(9.4) U06 * * −1 / 6 После интеграции、 Я ±(Б**) 7 /«= 0.00655 * х + С.(9.5 ’) Согласно граничному условию b * * = 0 prn x-0 передней кромки пластины, C = 0 найдено и последнее уравнение имеет вид Или= 0,0153 Бочонка, / 7. (9.6) Таким образом, толщина потери импульса турбулентного пограничного слоя, а следовательно и других условных толщин, увеличивается пропорционально расстоянию от передней кромки до 6/7 градуса, но в случае ламинарного слоя она пропорциональна квадратному корню из этого distance. As в результате толщина турбулентного пограничного слоя увеличивается быстрее, чем толщина ламинарного слоя.
Согласно формулам (9.5) и (9.6), коэффициент локального трения В этом случае напряжение сдвига Решение выше показывает, что при обтекании пластины только 1 эмпирическое отношение между функцией b ** * и т0 может быть использовано для определения сопротивления трению. Показано, что используемая форма этой связи соответствует распределению мощности скорости пограничного слоя. », / «О= (*//6) га、 при m = 1/11. Более точное приближение профиля скорости задается логарифмической зависимостью. Его использование требует более сложных расчетов и приближенных расчетов. Выполнив их, г. Шлихтинг получил интерполяционную формулу для коэффициента сопротивления. Ст = 0.455 /(1eKer8, (9.9) Это хорошо соответствует экспериментам с большим разнообразием чисел Рейнольдса.
- Результаты расчетов по формулам (9.8) и (9-9) близки друг к другу. Сравним сопротивление трения гладких пластин в ламинарной и турбулентной областях пограничного слоя. Если ламинарный и турбулентный пограничные слои существуют при одном и том же числе Рейнольдса Ke = 10′, то в соответствии с формулами (8.77) и (9-8)、 Так, в турбулентном режиме коэффициент лобового сопротивления примерно в 3 раза превышает ламинарный. Поэтому методы, описанные в работах [15, 28], направлены на поддержание ламинарного режима пограничного слоя на поверхности обтекаемого тела и предотвращение или задержку перехода к турбулентности. Если ламинарное сечение пограничного слоя на пластине нельзя считать пренебрежимо малым, то создаваемое им сопротивление необходимо учитывать, а точку перехода следует рассматривать как начало турбулентного layer.
In в этом случае уравнение (9.5′) может предполагать, что в точке перехода значение толщины b * * * равно ламинарному сечению и потере импульса турбулентного сечения. § »*=БТ *-^ Н *.Где 6″ * толщина потери импульса в точке перехода. По формуле(8.80) За исключением константы c、 б * * 7/6 _ bG7 / 6 = 0.00765 (п / г) −1/6(х-хп). (9.11) Вы можете использовать эту формулу для вычисления значения b **в любой точке раздела турбулентности, потому что вы знаете уравнение (9.10) до 6″*.Найти полную силу трения, суммируя сопротивление ламинарной секции и секции турбулентности. Px = 2ri%6 * * + 2ri! (6?* БГ) или РХ = 2ri026?*、 61 определяется по формуле x = I(9.11). Описанный метод расчета турбулентного пограничного слоя на пластине основан на эмпирической зависимости, полученной в гладкой пластине experiment.
Если ламинарное сечение пограничного слоя пренебрежимо мало, то уравнение хорошо подтверждается экспериментальными данными с большим числом Рейнольдса. Людмила Фирмаль
- In в реальных условиях течение по пластине (поверхности крыльев, лопастей, фюзеляжа) практически не происходит гидравлически smooth. As с течением в трубе, течение в турбулентном пограничном слое шероховатой поверхности приписывается одному из 3 modes. It имеет гидравлическую гладкость, а высота выступов на поверхности не влияет на сопротивление. На коэффициент сопротивления влияет как число Рейнольдса, так и режим шероховатости переходного или несовершенного выражения шероховатости; полное указание шероховатости или вторичное, от которого коэффициент сопротивления зависит только от шероховатости.
Смотрите также:
Возможно эти страницы вам будут полезны:

