Оглавление:
Расчет трубопроводной системы самотечного слива
Мы рассмотрим устойчивый, полностью установленный поток материала bingham через двумерный канал высотой h и предположим, что градиент давления ∂p / ∂x = −k отрицателен, что верхняя стенка (y = h) двигался в курсовой работе по гидромеханике в положительном направлении х со скоростью u и что сдвиг стенки Напряжение на нижней стенке (у = 0) больше предела текучести.
- Все остальные дела могут быть возвращены к этому делу. X и y компоненты Коши уравнение упрощается до ∂p ∂x знак равно ∂τ ху ∂y (6, 190) а также ∂p ∂y знак равно ∂τy у ∂y, (6. 191) поскольку в установленном канальном потоке
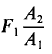компоненты девиатора напряжения не функции х. - Из (6. 191) мы заключаем p = τy y + f (x) (6, 192) и, используя (6. 190), мы видим, что f (x) = const = −k, что τ xy = −ky + τw, (6. 193) где τw — напряжение сдвига на нижней стенке системы с замерной установкой (y = 0).
Так как τw gt; ϑ, то материал течет вблизи стены, пока напряжение не упадет ниже предела текучести ϑ на высоте y = κ1h = (τw — ϑ) / k (6, 194) и материал становится твердым. Когда у становится больше, напряжение сдвига, наконец, становится отрицательным, пока в y = κ2h = (τw + ϑ) / k (6, 195) отрицательное напряжение сдвига −τ xy равно пределу текучести, после чего материальные потоки снова. Очевидно, что du / dy является положительным в первой зоне потока, так как мы сделать вывод из определяющих соотношений (3. 60) и (3. 62).
Для однонаправленных Нарушение конституционального отношения имеет вид τ xy = η1 du ду + ϑsgn дю ду (6. 196a) τy y = 0. (6. 196b) 198 6 Ламинарные однонаправленные потоки.
Из используя граничное условие u (0) = 0, мы получить распределение скорости в первой зоне течения как u u = — Х2 2η1u у час 2 — 2к1 год час, который для κ1 ≥ 1 уже является распределением по всему каналу. Людмила Фирмаль
В зона второго потока du / dy отрицательна, а распределение скорости u u = 1 + kh2 2η1u 1 — у час 2 — 2к2 1 — й час, (6. 198) где граничное условие u (h) = u было использовано. Как и ожидалось du / dy исчезает на поверхностях урожая. Скорость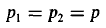
на поверхностях текучести y = κ1h и y = κ2h равна скорости твердого тела, которая из (6. 197) равна.
Примеры решения с методическими указаниями
| Решение | Лекции |
| курсовая | Учебник |
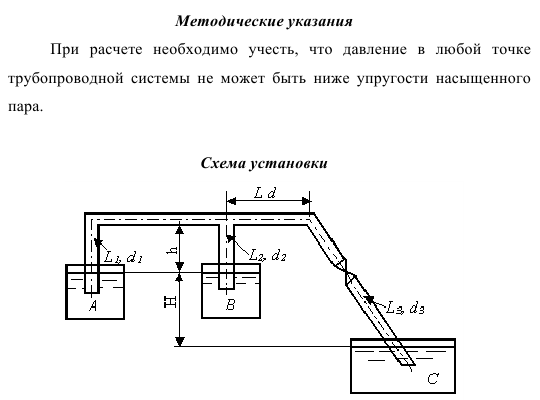
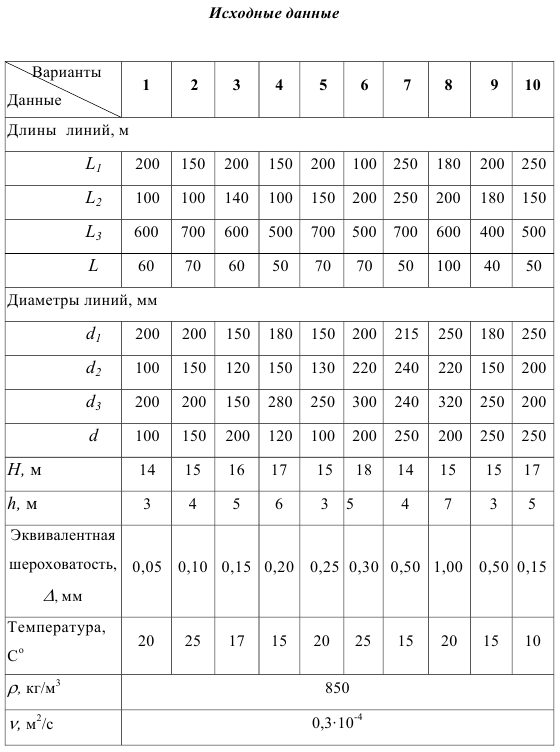
Содержание работы 1. Теоретическая часть. Теоретические основы гидравлического расчета сложных трубопроводов. 2. Расчетная часть. Расчет трубопроводной системы, служащей для слива воды из резервуаров А и В в резервуар С. Все резервуары промысловой системы открыты.
Определить расходы воды, поступающей в резервуар С при заданном напоре Н и коэффициентом сопротивления задвижки, температуре воды t и абсолютной шероховатости. Определить минимально возможную величину коэффициента местного сопротивления задвижки. Методические указания При расчете необходимо учесть, что давление в любой точке трубопроводной системы не может быть ниже упругости насыщенного пара.
