Оглавление:




Расчет статически неопределимых балок с двумя лишними неизвестными
- Расчет статически неопределенных балок С двумя дополнительными неизвестными Для расчета стационарных неопределенных балок необходимо составить два уравнения деформации, помимо уравнений статики. Общий случай этих уравнений совместно
включается в каждое уравнение. Неизвестный. Дважды порядок расчета статической неопределенной балки прослеживается на конкретных примерах. Для риса. 274, а жесткость балки на изгиб в первом пролете равна 2E. во-вторых, в правом пролете
концентрация силы R равна 1.In середина самого левого жесткого зажима Людмила Фирмаль
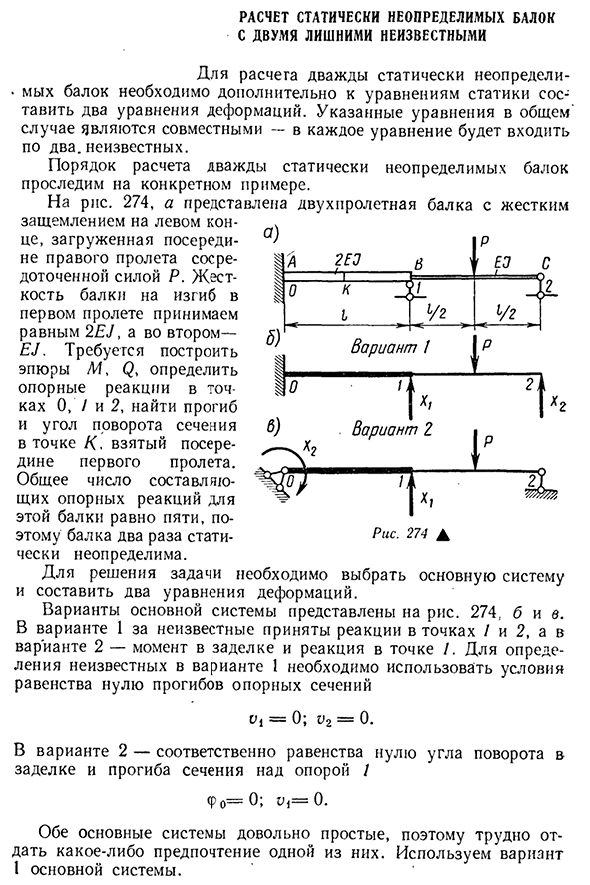
нагружена, а на втором спа требуется построить участок/и,(?Определите опорную реакцию в точках 0, 1 и 2, Сначала определите угол отклонения и поворота сечения в точке K, взятой в середине пролета. Общее число опорных реакций в композиции для этого
пучка в два раза статически неопределимо, поэтому оно равно пяти. Для решения этой задачи необходимо выбрать базовую систему и создать два уравнения деформации. Варианты основной системы показаны на рисунке. 274, Б и В. Для варианта 1 реакция в точках/и 2 неизвестна, а для варианта 2-реакция в момент уплотнения и в точке/. Для определения неизвестных параметров варианта 1
- необходимо использовать условие нулевого отклонения в секции опоры Опционы| / 2EE — Ньютон.—— В п К — б-б / 2 — ■& — б- / -2— В) Б Рис двести семьдесят четыре Но Тонны . Вариант 2 7-1 СФ=0;А2-0. В Варианте 2-угол поворота уплотнения равен нулю, соответственно и прогиб сечения на опоре/Fo=O;^1=0. Обе основные системы очень просты, поэтому трудно отдать предпочтение какой-либо из них. Возможность использовать меня в качестве основной системы. В
развернутом виде уравнение деформации для рассматриваемого случая имеет вид: — IX, » B^1 × 2 — °2=°2R ® 2X,®2X,~0 ‘ 1 (10.4 )) Здесь и a2p-отклонение основных точек системы 1 и 2 от внешней нагрузки P, и-отклонение точки 1 от неизвестных X^и X2\Ugh, и так далее. $ ^Ры б) 2х \ Один. П Д’ ■ * ГТТучастка М М Tightttttttt»— п Фигура Сюжет Х2 P1 0 2-й Ш И Л 4EE е) Что?! Рис 275А Для определения перемещений, содержащихся в уравнении (10.4), используется метод графического анализа. График основного момента системы(рис. Мощность 275, а) показана на рисунке из P, XI и X2. 275, b, C, G.
На рисунке показана фиктивная балка с фиктивной нагрузкой. 275d E. W. 1 Найти & 2p с Schr, из условия, что отклонение фактического Людмила Фирмаль
луча равно моменту воображаемого луча, показанного на рисунке. 275d: 1, 1П1, 2. 7ПП 2 + 2 * 2 5 / ‘ 3 1 ~ 24 а? 2^2 25/ . 1P1 1(1 2I\43PP + 2 ‘2 5 /’ 2 \ 2 + 3 ‘ 2 / ~ 48 • 5 / * 3122. Найдите V1L и Vp2xv, (см. Рисунок. 275e): _DLO) _ 1U1H, м ф~2’2e/ » 3 6Е/’ DL<2> _ _ _ _ 1 ^2х~т ф-2’2E / 3. Найдите A1x2 и V2x2(см. рисунок. 275, Ш): U1X2 Х2/,2_/_5х, П. 2 / 2. ‘3’ 12-й / * Х2/ Лл(2) _xx22//и3/U2hg-МФ- — — — — — — — — — 2E7-* ‘ — Т1 Два. Два. Х2/ 1. 2х^2/_. /. И==/ 2е / 3г / Если подставить в уравнение (10.4) значение, найденное после некоторой деформации прогиба)、 7P_4X1. 10х2=0; 43P-20X1-72X2=0. Когда вы решаете систему уравнений、 u37R.u_4R Л1-44г>У’2~с г’ После нахождения опорных реакций X4 и X2 их можно
рассматривать как внешние силы, и поэтому дальнейшие расчеты могут быть выполнены на статически определяемой консольной балке. Диаграмма момента и боковой силы(рис. 276, б и в) силы x b X2 и P(рис.Балка построена в обычном порядке по отношению к статически определяемым балкам, нагруженным 276, а). Для определения реакции уплотнения используются уравнения статики 313u=о/г=- / р. Как видно из сюжета момент, реактивный момент в печати выглядит так: =- д-Р1. Для определения прогиба и поворота поперечного сечения в точке K используется также
графоаналитический метод. На рисунке показана фиктивная балка с фиктивной нагрузкой. 276 г Прогиб сечения в точке K равен мнимому моменту этого сечения и мнимой боковой силе угла поворота•*:
Смотрите также:

