Оглавление:


Расчет статически неопределимых балок по разрушающим нагрузкам
- Расчет статически неопределенных балок Согласно нагрузке на перерыве Когда максимальное вертикальное напряжение самой прочной части балки достигает предела текучести, а для хрупких материалов расчет балки из таких стоячих максимальных
напряжений балки, однако, несущая способность балки, как и всех других волокон в этом сечении, как и в любом другом сечении балки напряжения, еще не исчерпана, но и не опасна.
При дальнейшем увеличении нагрузки на балку график напряжений критического Людмила Фирмаль
сечения изменяется и проходит через упругую и упругопластическую стадии. И только если напряжение равно пределу текучести всей секции, то несущая способность секции полностью исчерпывается. Такой участок, в котором все волокна подвергаются текучести, называется пластиковым шарниром (или пластиковым шарниром).
Формирование одного пластикового шарнира снижает степень статической неопределенности балки по одному, но еще не исчерпывает грузоподъемность всей конструкции. Полное истощение несущей способности балки соответствует образованию
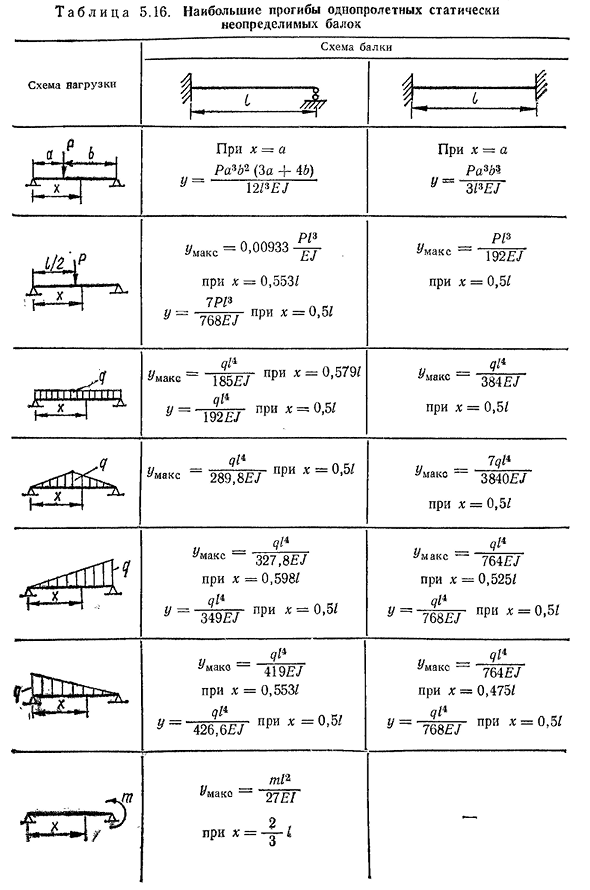
- нескольких пластических шарниров, которые превращают балку (или ее часть) в геометрически изменяемую систему. При расчете разрывной нагрузки принимается гипотеза о полной упругопластической работе материала на предельной диаграмме. 5.40 I1T а б л и Ц А5. 16. Максимальное отклонение однопролетной статической неопределенной балки Схема балок Как работает нагрузка Когда x=A Ppr2 (4-4&) 12PEJ Не X-a RA3. Г=3PEJ ^Макс=0.00933 х = 0.553/7P13 ■^7 6 8Э Т П Р Я ч = °>а с макинтошами Р-Р −192£7 Если
х=0,5/ // макс= Она весит 185 фунтов. Зет P RI h=>5 7 9 / X= = 0 ′ 5 в Y = ^E G/ // Макс 3 8 4£7 Если х=0,5/ у-Н-м» Qп Юмакс-289,8 ЭЖ х=0,5/7qP, АКО-3840E7x=0,5/ // Max 327, x, QEJ— 0,598/ ^ = — 3 4 ^ 7 p и x=015Z Юмакс — qP764EJ Когда х=0,525/ Семьсот шестьдесят восемь Если х=0,5/ // Макс=41г Ф/ ’ Х=0.553 / Qп 426.62-7П П и Х = ° ’ 5 / // Макс qP764EJ х=0.475/<?/ 4 При 768x=при 0,5 мм/ // Макс — Тр27е! В X 142 ′ предел текучести согласно закону крюка, площадь текучести бесконечна
(см. рис. 2.10). Например. Это позволяет определить разрушительную нагрузку балки. 5.40 утра=1G=I, EJ=const по всей длине луча. Решение. Людмила Фирмаль
Используя уравнение трех моментов, получают опорный момент MF — PT и строят график изгибающего момента. 5.40, б). Под наиболее напряженным участком-к-мощность П. Ожидается появление первого урожая в крайнем волокне. От условий Тринадцать. lV ’ (jr=L4max^1max^найти значение силы это происходит! п 64гот *Ж3 1max/’ График нормальных напряжений в сечениях k и 1 P=P1max показан на рисунке. 5.50 В. При увеличении мощности пластическая зона может быть удалена из секции(рис.) Растягиваться глубоко. 5.40 г), что приводит к появлению пластиковых петель в этом сечении (рис. 5.40, г). Балка находится в секции K. полезная нагрузка
балки еще не разряжена, хотя она станет статически определимой с ее шарниром. При дальнейшем увеличении нагрузки пластмассовый шарнир образуется на средней опорной вершине и при этом m s e h EN и K P= / ’ gmax увеличивает момент. Емкость нагрузки структуры вполне вымотана и изменяет к геометрически переменной системе. На рисунке показана балочная схема пластикового шарнира и диаграмма момента и напряжения. 5.40, например, G. разрывная нагрузка определяется из равенства изгибающего момента в двух наиболее напряженных сечениях /
GI1.Дж ^2М С s3z по Р7 _ —— 4—— где Wp=2SMaKC-для симметричного поперечного сечения относительно нейтральной оси, Wp= — ^SJ » B Spac-для асимметричного поперечного сечения. И так оно и есть. 6 г рот * 2 макс. / Разрывная нагрузка, которая определяется из условия максимальной грузоподъемности «ti P2max», больше расчетного допустимого напряжения: ^2 Макс 39Wp s^1 Макс 32’w В Пропорции зависят от формы сечения. Например, для прямоугольного поперечного сечения G p3 15 — ^ — = — g-и затем g» — y; для двутавровой балки 1,16 грузоподъемность увеличивается на 38%.
Смотрите также:
| Неразрезные равнопролетные балки с симметричными вутами | Балки равного сопротивления |
| Перемещения в статически неопределимых балках | Обратная задача теории сооружений |

