Оглавление:



Расчет полей по методу сеток
Вычислить поля, используя метод сетки. Метод сетки — это численный метод интегрирования дифференциальных уравнений в частных производных путем сведения их к конечно-разностным уравнениям.
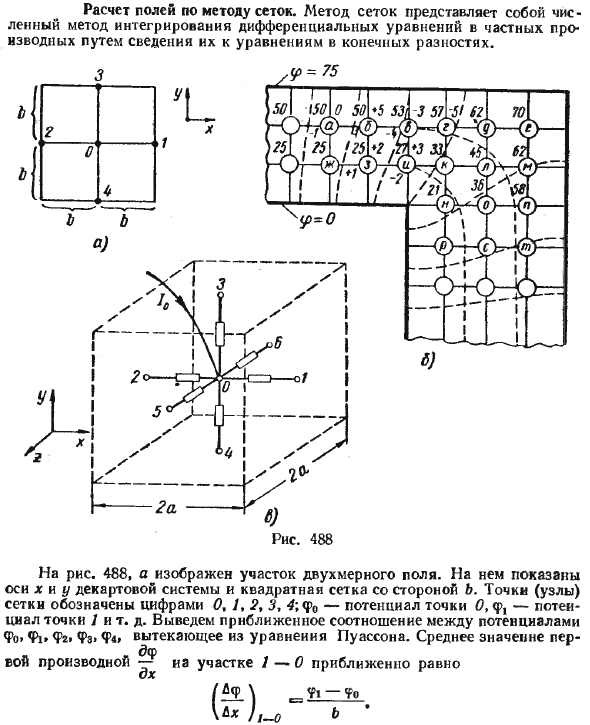
- На рисунке 488 показан двухмерный график поля. Отображается квадратная сетка декартовой системы осей x и y и стороны b. Точки сетки (узлы) обозначены числами 0, /, 2, 3 и 4, φ0 — это потенциал в точке 0,
φ — это потенциал в точке 1 и т. Д. Людмила Фирмаль
Приближенное соотношение между потенциалами Фо »Ф1» Фг »Фз» Ф «» Из уравнения Пуассона. Среднее значение производной d в диапазоне от -1 до 0, oX / DF \, в сегменте 0-21 приблизительно равно / rT ~ ^ go \ Ax Jo-3 ‘вторая производная-первая производная в точке 0
Приблизительно равно разнице между средними значениями в секциях 1-0 и 0-2, см. Расстояние b между серединами сегментов 1-0 и 0-2, т. Е. Y * O o \ A * / o-2 b b dx * ~ Bx * ~~ b b ba Нравится 0 *? _Uz-Oud ~ 2Uo do> ~ b *
- Напишите уравнение Пуассона двумерного электростатического поля dx> du * e ‘P / t «Свободный заряд d2 в точке 0 m5? II l 9svob & yr 4-? I 4 «Uz 4-? <- *? O- •• (d) Если поле С описывается уравнением Лапласа, pfet> 5 = 0 n Yi 4-? 2 4-Uz 4 -Y <-4y0 = 0. (b) Уравнения (a) и (b) дают связь между квадратными потенциалами решетки.
Это основа метода решетки. Уравнение (а) или (б). При расчете с использованием метода сетки используются не только квадраты, но и другие типы сеток (например, полюсы). Как правило, они имеют
свои собственные формулы с конечными отличиями, которые отличаются от формул (а) и (б). , Людмила Фирмаль
Двумерные поля в соответствии с уравнением Лапласа окружены конкретными поверхностями, и потенциалы этих поверхностей известны (задача Дирихле), или известно значение производной потенциала, перпендикулярного каждой границе раздела в каждой точке. (Проблема Неймана).
Значение потенциала одной части интерфейса известно, а нормальная производная потенциала известна в другой части. Вам нужно найти потенциальное значение прямоугольной сетки для этого поля.
Последовательность вычисления для задачи Дирихле показана на примере расчета поля, образованного двумя параллельными прямыми углами на рисунке. В точке поворота 488b расстояние между параллельными сторонами угла изменяется.
Верхний потенциал установлен на 75 единиц, нижний предел-ноль. Предположим, что нет космического заряда. 1. Примените тонкую квадратную линию к квадратной сетке. Результирующий квадратный узел обозначается буквами a, b, c, d, dt … (обведено кружком).
2. Следующий этап расчета состоит из произвольного выбора потенциалов для узлов a, b, c, … Объем дальнейшей вычислительной работы сильно варьируется в зависимости от того, насколько вы близки к фактическому начальному распределению потенциала.
Поэтому вы должны стремиться максимально распределить наиболее вероятные начальные возможности. В этом примере для этой цели нанесите приблизительный курс силовых и эквипотенциальных линий и приведите к этим линиям, чтобы записать начальное значение потенциала узла (числа слева и сверху каждого узла) ,
3. Для каждого узла найдите оставшееся значение уравнения (b). Следовательно, остаток от точки b равен 53 -b 50 + 75 4’25-4 * 50 = 3. Запишите остаток суммы в верхнем правом углу каждого узла *. 4.
Остаток каждого узла должен быть равен нулю, поэтому более трудоемким шагом вычисления является изменение потенциала узла, чтобы все остатки узла не превышали определенного значения (например, 1 или 2).
Это Для этого измените потенциал примерно на одну четверть от остатка (в этом случае уменьшите потенциал на 1 в точке b) в одной из точек с наибольшим максимумом и оставьте его на всех других узлах. Пересчитать базу.
Вновь полученный остаток записывается в нижнем левом углу каждого узла (показан не на всех диаграммах). Такие операции выполняются несколько раз, пока все остатки не станут меньше или равны указанному значению. Процесс сходился. При расчете с помощью калькулятора.
Этот метод может быть применен к магнитным и электрическим полям, линейным и нелинейным средам, постоянным и изменяющимся во времени полям. Более подробную информацию о методе сетки можно найти, например, (L. 26). • В верхнем правом углу 488, b точки b на рисунке должно быть число -b, а не 5,
Смотрите также:

