Оглавление:



Расчет на сжатие с учетом устойчивости
- Расчет компрессии с учетом устойчивости При расчете металлических и деревянных брусков, действующих на сжатие, используется устойчивое состояние С=^ — <[Г] Г,(8.15) Где N-продольная сжимающая сила, а[a]y-допустимое напряжение при расчете
устойчивости. [o] y=[<t]SJ•<p, (8.16) где f-коэффициент уменьшения допустимого напряжения сжатия с учетом запаса устойчивости(табл. 8.13). Формула 189 является Так как Fqp-f[St] ’ (8,1 7) в (8.17) имеет два неизвестных GBR и f,
Выбор раздела выполняется Людмила Фирмаль
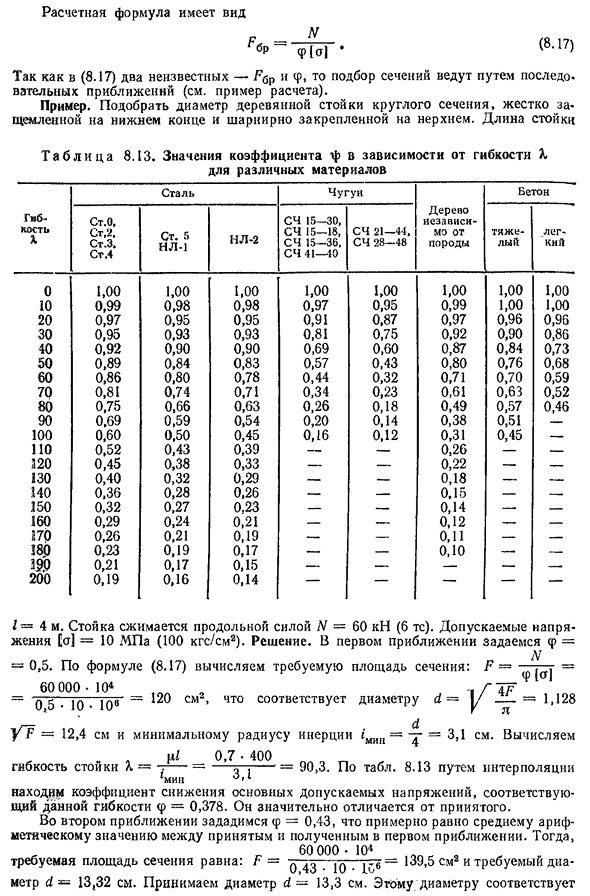
последо. приближение стелфа (см. пример расчетов). Например. Подобрать круглую деталь деревянного стеллажа диаметром плотно шарнирно закрепленную на нижнем крае и шарнирно закрепленную на верхнем. Длина стоек Т А Б Л и Ц А8. 13. Значение коэффициента Ф в зависимости от гибкости для различных материалов
Гибкость% Сталь чугун Независимо от породы, дерево Бетон St 0, ST 2, St Z. Статья 4 Санкт-5NL-1 NL-2 СЧ15-30, СЧ15-18, СЧ15-36, SCH41-40 СЧ21-44, SCH28-48 Тяжелый Легко 0 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 10 0.99 0.98 0.98 0.97 0.95 0.99 1.00 20 0.97 0.95 0.95 0.91 0.87 0.97 0.96 0.96 30 0,95 0,93 0,93 0,81 0,75 0,92 0,90 0,86 40 0.92 0.90 0.90 0.69 0.60
- 0.87 0.84 0.73 50 0.89 0.84 0.83 0.57 0.43 0.80 0.76 0.68 60 0,86 0,80 0,78 0,44 0,32 0,71 0,70 0,59 70 0.81 0.74 0.71 0.34 0.23 0.61 0.63 0.52 80 0.75 0.66 0.63 0.26 0.18 0.49 0.57 0.46 90 0.69 0.59 0.54 0.20 0.14 0.38 0.51 — 100 0.60 0.50 0.45 0.16 0.12 0.31 0.45 — 110 0,52 0,43 0,39 — — 0,26 — — 120 0,45 0,38 0,33 — — 0,22 — — 130 0,40 0,32 0,29 — — 0,18 — — 140 0,36 0,28 0,26 — — 0,15 — — 150 0,32 0,27 0,23 — — 0,14 — — 160 0,29 0,24 0,21 — — 0,12 — — 170 0,26 0,21 0,19 — — 0,11 — — 180 0,23 0,19 0,17 — — 0,10 — — SW0. 21
0.17 0.15 — — — — — 200 0.19 0.16 0.14 — —» — — ! = 4 м. стойка сжимается продольной силой N=60kN (6TS). Допустимое напряжение[o]=10 МПа (100 кгс / см2). Решение. Для первого приближения установите f=N = = 0,5. По формуле (8.17), рассчитать требуемую площадь поперечного сечения: Ф =60 000-104i/ ’ 4Ф=вопрос: показывает все виды раздражающих предупреждений,|
В6=120cm2, соответствует диаметр D=г — =1,128=12,4 см и минимальный радиус Людмила Фирмаль
инерции объектов: г=-3,01 см. Расчет c / 0,7 * 400 мм стойка A.= ——= —— 5—j—— — 90,3 я не уверен. Согласно таблице. 8. 13 интерполированный fMHH15 ′ 1 определяет основной допустимый коэффициент уменьшения напряжения, соответствующий этой гибкости f-0,378. Это очень отличается от принятого. Во втором приближении мы даем f=0,43, что принимается в первом приближении и приблизительно равно среднему арифметическому между полученными значениями. Тогда 60,000 * 104 Требуемая площадь поперечного сечения равна: F=1_b^~cm2 и t^Uem11a Di a ’ метр d=13j32cm. Примите диаметр d=13,3 см. Этот диаметр соответствует Минимальный радиус инерции iMHH=d / 4=3,325 см. Гибкость стойки х= — = 84.2, а соответствующий
коэффициент<Р=0,446(см. табл. 8.13). Ряд напряжения тока 60,000/kg: o==9.7 MPa|9 7 — 2-!. Пониженное напряжение допускается на 3%. Например. Для стойки с одним зажимом и другим свободным концом длина стойки I составляет 8239-72, если стойка I составляет 1,5 м, то усилие сжатия N=500 кн(50ТС), допустимое напряжение сжатия[а]=160 МПа (1600. Для выбора раздела используйте формулу (8.17). Установите CP=0.5. Тогда требуемое сечение будет выглядеть так:500 * 103 • 104 0.5■160 ■ 106 =62. 5cm2. Согласно ассортиментной таблице, двутавровая балка № 36; F=61,9 СМ1, g, 2•150/, выписывают данные. Н — ■2.89 см. Рассчитайте гибкость стойки L= • 2 89 ″ = ^^,8.
Согласно таблице. 8.13 X=103,8 с помощью линейной интерполяции находим CP=0,57. Расчетное напряжение принимаемого участка выглядит следующим образом:500 • 103 • 10* 0.57•61.9 =141,7 МПа (1417кгф / см2), что на 11% меньше допустимого напряжения. Возьмем двутавровую балку № 30А, площадь поперечного сечения которой составляет 49,9 см2,а минимальный радиус инерции-2,95 см. С этим поперечным сечением, гибкость шкафа является следующим: _2■150 2.95 101,7 тогда в зависимости от таблицы. 8.13 КП=0.59. Напряжение тока-g-gg-49 9 — =^98 кгс / см2, которое 6% более высоко чем допустимое. В пределах диапазона, заданного при этих условиях, более крупная задача аппроксимации не может быть получена. Осталось присвоить двутавр номер 36.
Смотрите также:

