Оглавление:









Расчет на прочность при изгибе
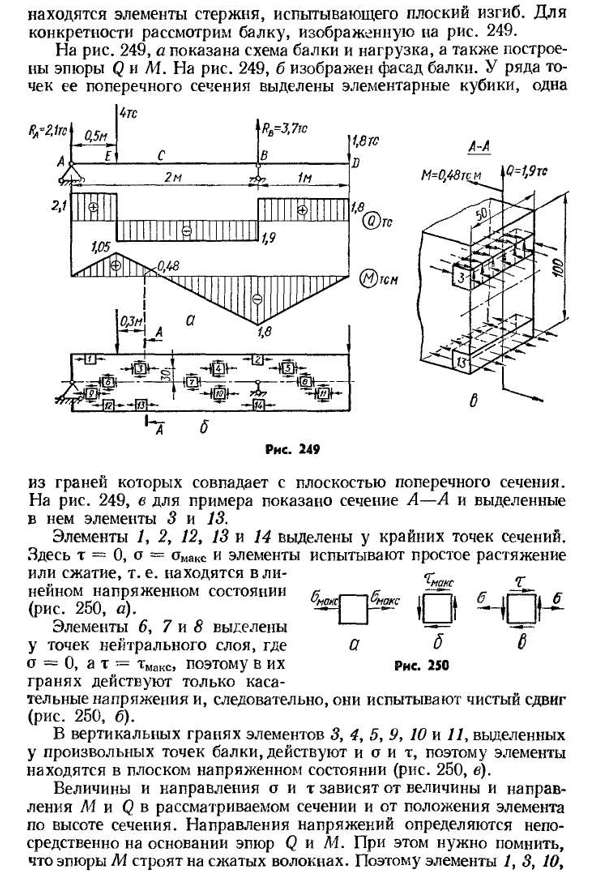
- Расчет прочности на изгиб В предыдущем абзаце этой главы была получена формула для расчета А и Т плоского изгиба балки. Эти формулы позволяют создать необходимые условия прочности для просмотра и выбора участков деталей, которые будут работать с изгибами. Чтобы получить эти условия, выясните, в каком стрессовом состоянии Имеется 252 элемента стержня, испытывающих плоский изгиб. В частности, рассмотрим луч, показанный
на рисунке. 249. Для риса. 249, и показаны схемы балок и нагрузок, а также графики Q и M на рисунке. 249, b показывает переднюю часть луча. В некоторых точках его поперечного сечения находятся основные Кубы Двести сорок девять 5 часов вечера. Он совпадает с плоскостью поперечного сечения своей плоскости. Для риса. Например, 249 указывает раздел A-A и присваивает его элементам 3 и 13. Элементы 1, 2, 12, 13 и 14 выделены в крайних точках раздела. Здесь t=0, o-o^max и элементы испытывают простую
растяжку Г б ^Макс^Макс|| б Или сжатие, т. е. в линейном напряженном Людмила Фирмаль
состоянии (рис. 250, а). Поскольку элементы 6, 7 и 8 выбраны в точке нейтрального слоя, где o=0 и t=Tmax, на поверхность действует только касательное напряжение и, таким образом, происходит чистый сдвиг. 250,6). В вертикальных плоскостях элементов 3, 4, 5, Р, 10 и 11 элемент находится в плоском напряженном состоянии, так как он выбирается в любой точке балки и действует с О и Т(фиг. 250, в). Величина и направление O и t зависят от величины M и Q в рассматриваемом сечении и положения элемента в направлении и высоте сечения. Следует помнить, что направление напряжений определяется непосредственно на основе участка Q, а участки M строятся на сжатых волокнах. Итак, элементы/, 3, / O, 25314 с
11 опытом сжатия и элементами 9, 12, 13, 4, 2, и 5 испытайте напряжение. Чтобы определить направление t, обратите внимание на знак Q в соответствующем разделе. Например, сечение A-A Q отрицательно, и поэтому, если вы попытаетесь повернуть обе части рассеченной балки против часовой стрелки, левая сторона сечения вверх (С Q равным 249.). Итак, t направлено вправо от элемента 3.in в других плоскостях в направлении t касательная определяется законом парных напряжений. Значения напряжений можно найти в формулах, полученных в предыдущем пункте: а)для элементов 1,2, 12, 13 и 14 Сделай — b) для элементов 6, 7 и 8 л.7. Ч-Макс — СМО
- П «Самый большой Q. От F до Jb • С)3, 4, 5, 9, 10 и для элементов Если балка имеет прямоугольное поперечное сечение, например, с размерами, показанными на рисунке. 249,в, то B=5 см; H=10 см; Ф=50CMG; Фе=л, 5;Ш=см3=83. 3 см3; J= — ^ — cm4=4 1 7 CM4. Тогда элементы 2 и 14(|A11=1,8 TS * m=180 000KGE * cm) Бонус-180000 83.3 кгс / см2=2160 кгс / см2; Для элемента 7(|Q / −1,9 TC=1900KGE) Тмакс 1,5 тысячи девятьсот Фитти. кгс / см2=57 кгс / см2; для элемента 3 (M-48 000KGE*CM; / Q / =1900KGE) y-3cm; S= (5 — 3) • 5 • [z=см3=40 см3;= — кгс / см2=345 кгс/см2; t=кгс / см2=37 кгс / см2 И так далее. Таким образом, при поперечном изгибе балки материал находится в состоянии неравномерного плоского напряжения. Риск указывает на то, что
необходимо описать условия прочности 2s4bal, а именно точка, в которой материал находится в наиболее напряженном состоянии. Опасным будет один из следующих трех пунктов. а)точка, в которой нормальное напряжение достигает наибольшего значения б)точка, в которой касательное напряжение достигает наибольшего значения в) в момент, когда C и t принимают наибольшее значение, таких точек может быть несколько. Первая точка расположена в крайних волокнах сечения, где изгибающий момент является наиболее важным(например, точки На рис. 2 и рис. 14). 249). Напряженное состояние в таких точках является линейным рис.
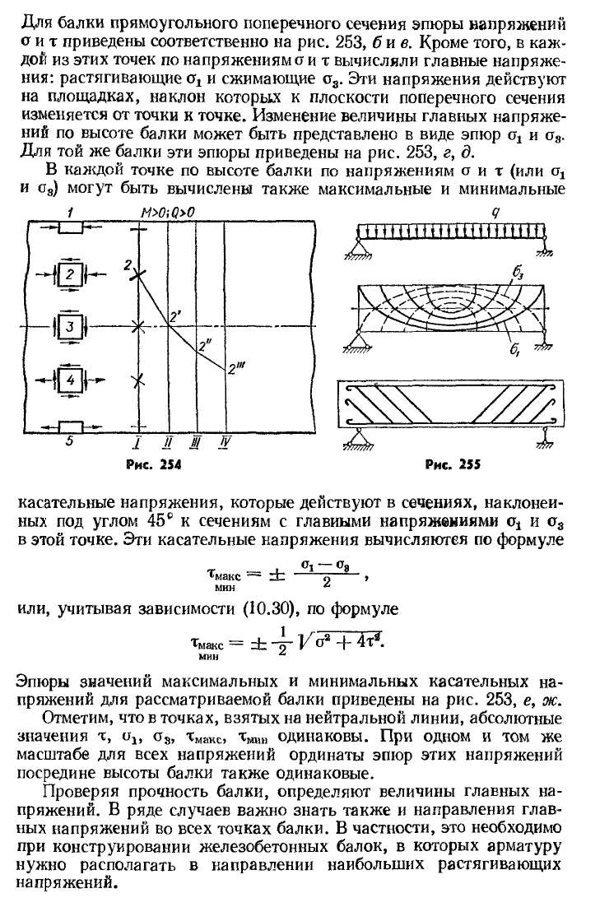
250, А) и условия интенсивности записываются в виде ом<с= < М.(10.28)вторая точка находится на нейтральной линии сечения Людмила Фирмаль
с наибольшей боковой силой (рис. 249 это точка 6 и все в любой точке-нейтральный слой, где Q=QwaKC). В такие моменты чистый сдвиг(рис. 250, б), следовательно, условие прочности будет иметь вид tyax=Qm8i^ — т — =к<[г]. (10.29) что касается третьего пункта, то его позиция не ясна. Но там, где она выбрана, существует плоское напряженное состояние (рис. Основное напряжение рассчитывается по формуле 250, b) <4=+г°г+4×2 1; О2=0;О3=~[о-V О2-g4T2]. (10.30) Эти значения вводятся в уравнение эквивалентного напряжения при различных теориях прочности((7.2), (7.6), (7.11), (7.20), (7.21)], получите требования к прочности Оэкв! =»[о+]/О2-я-выводам 4t2]<[о]; Ozkvp= — С±П/О2 -}-выводам 4t2<[о]; ое=У О а-я-выводам 4t2<[а];в Вт V=с V О2+Zt2<[о]; Аренда=±1~2+4×2<1°1> (10.31) (10.32) (10.33) (10.34)) (10.35 утра)) 25sgde Для расчета балок из термопластичного материала рекомендуется использовать условия прочности, полученные по теории III и IV [уравнения (10.33) и (10.34) 1]. Подавляющее
большинство примеров, практикующих применение и расчет луча, показали, что реальной угрозой является крайняя точка этого участка, где M=φ 4↑. Поэтому проверить расчет прочности балки практически можно следующим образом: 1) Найти сечение с опасным поперечным сечением, то есть максимальное абсолютное значение изгибающего момента Mmax;2. проверьте расчет прочности балки.) Согласно этой схеме, для большинства профилей(круглых, прямоугольных, двутавровых и других сечений) расчет конструкции прост, в этом случае условие прочности (10.28) рассчитывается следующим образом: Макс. (10.36)) Определите необходимый момент сопротивления балки и, приняв определенную форму поперечного
сечения, выберите ее размер. Рассмотрим несколько примеров расчета балки на основные условия долговечности. Пример 39. D-лабораторная балка(рис. 251) определить допустимую нагрузку[Р] С учетом значений заданных размеров Z, D и d и допустимого напряжения[о]. Опасный участок, очевидно, находится в поглощении и является a / M ax=P1. Момент сопротивления в данном случае НД * 32 (1-А4); Опасной точкой балки будут верхняя и нижняя секции уплотнения. Запишите условия силы для них, мы получим Триста двадцать один И Макс- 3 2I g -, — l O Z(1-4) отсюда находим допустимую нагрузку: П<[П ] — л Р8 (1-4) [ст] Пример 40. На балке (рис. 252) нагрузка 10TC, равномерно распределенная пядь. Материал луча STZ ([o]=1600 кгс / см). Потребности Выберите 256 различных поперечных сечений. На чертеже горизонтальная центральная линия обозначает
нейтральную линию. Опасный пролет, будет ли раздел в середине q? м т-1р п10 000-АКС 160мм= = — § — =~г» = ————§———- К Г ссм㎡=200000 кгс см. <[o]=1600 кг / см2. Точка опасности — это точка этого участка, самая дальняя от нейтральной линии. Требования к прочности для них следующие: Mmax 200 000^max C / отсюда находим необходимое значение момента сопротивления: 200 0001OC — ^^1G00CM25cm * найдено, gstrtsp Есть перенапряжение (O0>0) или пониженное напряжение (60<0 Р °W l I/ 6 ° = ——— м———-1 0 0% » L4M ° * M ax Ht1max Макс. М4″ г г г». Ww_C7 1г При прочностных расчетах отклонение расчетного напряжения от допустимого должно быть в пределах±5%от допустимого напряжения. Для сравнения веса балок различных сечений, учитывая, что вес пропорционален площади F
поперечного сечения, мы также вычисляем значение F. Для большей ясности, поперечное сечение Перейдем к расчету:1. Это будет объяснено. 252, a, TT/ / 3W>125cm3;D>D-и C-m=но принимают мм; и = — 32Р= 13015 6″ = 1 2 5 130,50 ’5 100% = ~ 4 > 2% | Макс. д% б см=10.83 см. 9 8-2770 Как Секция 2H2, показанная на рис. 252, б, W=b (26)2=2>125 B s m B 7 2 см< О принять около b=6 см=60 мм; — тогда V=2_. 6’cm3=144 см’; о — И еще= — — 2 5 1 4 4 14^ — 1 0 0% = — 13,2%; G=6 * 12см®=72см®. 3. Это будет объяснено. 252, e, W= — 2 ^ — ^ — = 2 — BZ>125 см3; B> / <375 см=7,21 см. Примите B=7.5 cm=75mm; тогда W=2-7>5’cm ’= * 4° — 5cm3;6o= * −12^ — 7o54o~ » 100%=~11g=7, 5 * ®=112.5 cm. 4. Рассмотрим поперечное сечение в виде двутавровой балки(рис. 252, е). Затем возьмите двутавровую балку № 18 195_ _ 14Q
Смотрите также:
| Нормативные и расчетные сопротивления материалов | Формула Эйлера для критической силы. |
| Коэффициенты условий работы и коэффициенты надежности | Кинематически возможные состояния. |

