Расчет критической температуры по известным плотностям жидкости при двух температурах (два экспериментальных значения)

Расчет критической температуры по известным плотностям жидкости при двух температурах (два экспериментальных значения)

Расчет критической температуры по известным плотностям жидкости при двух температурах (два экспериментальных значения). Когда я преобразовал уравнения Ytvos и Segden, Smith, Greenbaum и Rutledge [12], я получил зависимость. (1У-30） Где Tkr-критическая температура жидкости,°К. п! Плотность жидкости при температуре°к; Ra-плотность жидкости при температуре T2°K. Используя формулу(1U-30), можно определить критическую температуру с относительно небольшой погрешностью, но это только в небольшом диапазоне температур. Чтобы получить значение, близкое к истинному значению Tcr, необходимо выполнить следующие условия: (1У-31） Средняя погрешность расчета Tcr по описанной методике составляет около 3%. Если… п = 0.63945 г / РМЖ Р2 =! 0.62470 г (ЦМГ Г= 273,2°And22 = 288,2° Пример IV -!!。Определите критическую температуру T? 2-метилбутан Решение.

Подставляя данные в Формулу(1U-30), получаем: Т 288.2-273.2, ПВО 0 、、 ГкР〜т0. 63945\10зг+ 288 * 2 +б-465К \ 0.6247 о] 1 Экспериментально получено G,; p =461р0<sup class=»reg»>®</sup>K. несмотря на то, что условие (1U-31) не выполняется, погрешность расчета, равная+ 0,9%, невелика. Как определить плотность жидкости при температуре T1 p *и при температуре T2 когда pg задается Tkr он предложил следующую формулу: Р = p0p(рН [))(1У-32） В предположении, что плотность жидкости зависит только от температуры, при которой она упала, T = T / Tcr, и график функции Φ (Gpr) аналогичен, только liquid. At при низких давлениях это предположение справедливо для очень больших групп веществ.

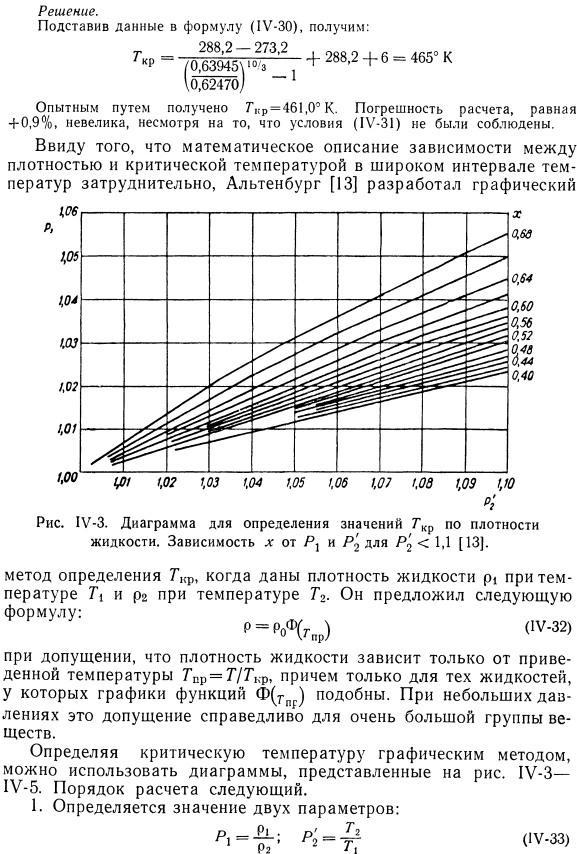
Альтенбург разработал график в связи с тем, что трудно математически объяснить связь между плотностью и критической температурой в широком диапазоне температур. Людмила Фирмаль

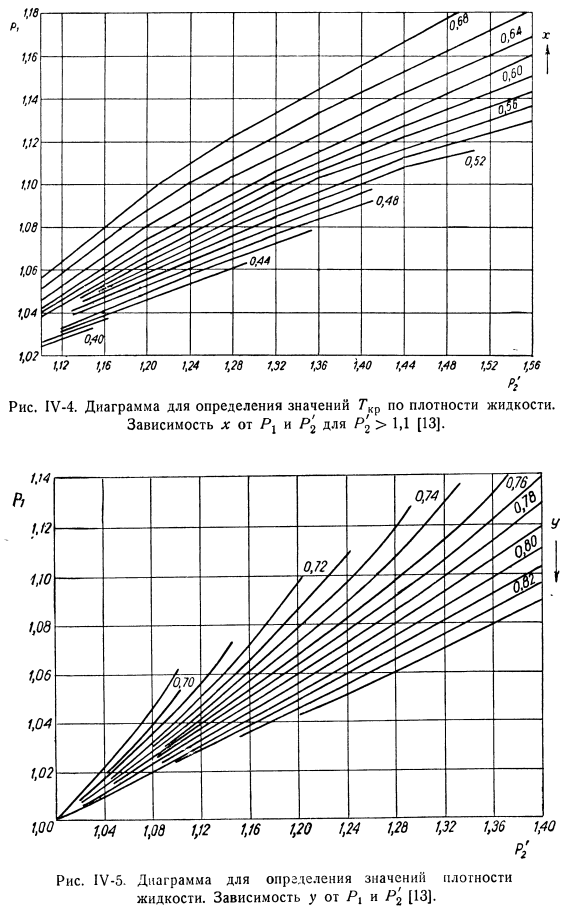
• Для определения критической температуры с помощью графического метода можно использовать схему, показанную на рисунке. 1У-3-1У-5.Процедура расчета выглядит следующим образом: 1. Определены значения 2 параметров. 2.Значение x = T2 / Tcr рассчитывается в соответствии с диаграммой. Для IV-1 * P ’ 2 <1.1*, для рис. 1U-2, P2> 1.1. 3.Согласно рисунку, 1U-3 считается как e / = p * / po. 4.Стоимость рассчитывается Ч = по = г(| г-34> расчет величины p0 позволяет определить плотность жидкости при любой температуре в дальнейшем. 1U-5 значение y. средняя погрешность расчета 7, f составляет около 1,5% (максимальное значение не превышает 5%). Пример 1 \ М2.Если вы знаете плотность толуола, определите критическую температуру Tnr толуола. 7 \ «281.2°K p», 0.878 г / см3 Решение. 1. Расчет параметров： _ 0.878 1 0.780 1.126; Р, _ 383.2 НГ-281.2 1,363. При Г2 ″ 383,2°Kp2 = 0,780 г / см3 2.Обратный отсчет по цифре: 0.642. г-0.766. ГКР.383.2. 0.642. = 596°к; Р0 = 0.878 0.766. = 1,145.

• Следовательно, экспериментально найденное значение составляет 593,8°К. Погрешность расчета составляет+ 0,37%. Помимо того, что описано, существует множество других способов определения менее важных параметров, но они здесь не учитываются ни из-за низкой точности, ни из-за большой сложности. В работах Херцога [14], Воулза, Риделя [3], Яткара и Лаксминараяна [15], Нокея [16] рассматриваются методы расчета критических констант на основе известных структурных формул вещества. В научной литературе описаны способы расчета ключевых параметров при известных физико-химических свойствах вещества. Ридель [3]предложил метод расчета t’cr ’ Rcr и UMcr, а также критического параметра CCR из 2 известных значений давлений насыщенных паров при температуре Tx и T2 (px и p2) и 1 значения плотности жидкости p при температуре T. Также был разработан расчет method.

At температуры Tx и T2, T, f, а также давление насыщенного пара PX и p2 известны в случае pkr. Расчет по этим методикам достаточно сложен. Выполнение расчетов по методу Филиппова[11]несколько проще и быстрее. Это говорит о том, что критические параметры tkr1, P » определяют значение P или известную температуру кипения Hnip, а также 2 значения плотности жидкости p0 и p! При температуре T0 и T1, или если температура кипения равна 7 * bn, давление пара при температуре T ^p1 и плотность P0 жидкости при 7 * 0 Все эти методы проиллюстрированы и проиллюстрированы на примере монографии [17]. 1 ^ Ktkrrkr ГРКР Мркр 3.83.; Что это? РКР. 3.95. (ГУ-35）

В низкотемпературном диапазоне, если плотность пара пренебрежимо мала по сравнению с плотностью жидкости, уменьшение плотности жидкости является приблизительно линейной функцией снижения температуры. Людмила Фирмаль

• Филиппов [18] также предложил упрощенную формулу расчета критической постоянной, основанную на предположении, что плотность p p жидкости на насыщенной линии является функцией перепада температуры T p p и практически не зависит от значения критерия решения (проверено на многочисленных примерах) (георадар-0,6 нашел максимальное отклонение±2,8%).Филиппов, согласно правилу Кайета и Маттиаса, экстраполирует значение плотности переохлажденной жидкости Р0 на температуру абсолютного нуля и отмечает, что отношение х = по / ПЦР примерно равно значению критического коэффициента (максимальная погрешность составляет 3 раза).％） −3.95-1.95 РКР * КР(1У-36） Филиппов рекомендовал его

Смотрите также:

Решение задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Аддитивный расчет критической температуры.
2. Аддитивный расчет критических параметров на основе экспериментальных значений некоторых физико-химических величин.
3. Выбор метода расчета критических параметров чистых веществ.
4. Псевдокритические параметры.