Оглавление:




Расчет косозубой цилиндрической передачи на прочность
- Расчет прочности винтовой передачи Прочность зуба винтового колеса определяется его формой, нормальными размерами поперечного сечения и длиной зуба. Была введена концепция эквивалентного колеса, чтобы унифицировать, как рассчитываются прямые и диагональные зубья. При расчете прочности винтовые зубчатые колеса обычно заменяются цилиндрическими цилиндрическими зубчатыми колесами одинаковой прочности.
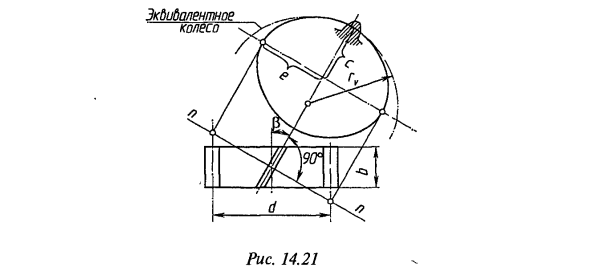
Кроме того, эквивалентный модуль колеса mv и нормальный модуль спирали tp равны длине зубца колеса (b = bv) y, а радиус эквивалентного круга колеса имеет поперечное сечение цилиндрического зубчатого колеса с делением винта в плоскости nn. Максимальный радиус кривизны результирующего эллипса (рис. 14.21). Полуось эллипса, полученного в поперечном сечении, равна c = d / 2 и e = d / (2 cosp), где d — диаметр шага окружности винтового зубчатого колеса. (Угол наклона 3 зуба.
Эквивалентным цилиндрическим зубчатым колесом является колесо с формой и размером зуба, которые приблизительно соответствуют форме зуба и размеру винтового зубчатого колеса с нормальным поперечным сечением. Людмила Фирмаль
Из геометрии анализа видно, что максимальный радиус кривизны эллипса равен rv = e2 / c = d / (2 cos2 p). Тогда эквивалентный цилиндр разделить диаметр цилиндра dv = 2 rv = d / cos2p и эквивалентное число зубьев колеса Zv = dv / mn = d / (mn cos2 p) = z / cos3 p, Здесь d и z — диаметр разделенного цилиндра и число зубьев винтового зубчатого колеса. Уменьшенный радиус кривизны ppr = g / sin a / (2 (g / ± l) cos2P); общая длина линии контакта / = mab / cosp. То же самое верно для вывода зависимостей для выполнения расчетов прочности для цилиндрических прямых и винтовых колес. Наклонное расположение зубьев дает винтовым зубчатым колесам и зубчатым колесам множество положительных характеристик, которые учитываются при расчете, таких как повышенная прочность и гладкость.
В связи с этим при определении напряжения изгиба используется формула (14.12), но с коэффициентом, учитывающим наклон зубов. ^ = (1-МП / 120))> 0,7, Где £ p = b / px — коэффициент осевого перекрытия. b-ширина короны (рис. 14.21); px-p, / sinp-осевой шаг; p, -круговой шаг концевой секции. Тогда уравнение для верификационного расчета винтовых зубчатых колес, связанных с сопротивлением усталости при изгибе, имеет вид 2 T {KpYFY ^ oF = —- scRadm, Где Yf — коэффициент прочности зуба (выбирается в соответствии с эквивалентным числом зубьев zv) ‘, а mn — модуль нормальной винтовой зубчатой передачи. При расчете винтовых зубчатых колес с использованием контактных напряжений с использованием уравнений (14.19) и (14.20) наклон зубьев учитывается коэффициентом формы сопряженной поверхности ZH. Для косозубых колес ZH = ^ / косп / (cosa si na). Коэффициент, учитывающий общую длину линии контакта, Zs = y [Sof.
Смотрите также:
Решение задач по прикладной механике

